目录
- 一、固定费用问题案例解析
- 1.1、固定费用问题(Fixed cost problem)
- 1.2、案例问题描述
- 1.3、建模过程分析
- 1.4、PuLP 求解固定费用问题的编程
- 1.5、Python 例程:固定费用问题
- 1.6、Python 例程运行结果
- 二、PuLP 求解规划问题的快捷方法
- 2.1、PuLP 求解固定费用问题的编程
- 2.2、Python 例程:PuLP 快捷方法
- 2.3、Python 例程运行结果
一、固定费用问题案例解析
1.1、固定费用问题(Fixed cost problem)
固定费用问题,是指求解生产成本最小问题时,总成本包括固定成本和变动成本,而选择不同生产方式会有不同的固定成本,因此总成本与选择的生产方式有关。
固定费用问题,实际上是互斥的目标函数问题,对于不同的生产方式具有多个互斥的目标函数,但只有一个起作用。固定费用问题不能用一般的线性规划模型求解。
一般地,设有 m 种生产方式可供选择,采用第 j 种方式时的固定成本为 \(K_j\)、变动成本为 \(c_j\)、产量为 \(x_j\),则采用各种生产方式的总成本分别为:
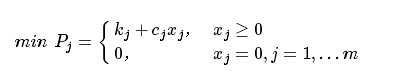
该类问题的建模方法,为了构造统一的目标函数,可以引入 m 个 0-1 变量 y_j 表示是否采用第 j 种生产方式:

于是可以构造新的目标函数和约束条件:
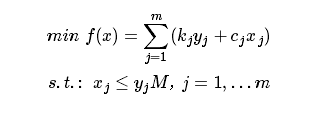
M 是一个充分大的常数。
1.2、案例问题描述
例题 1:
某服装厂可以生产 A、B、C 三种服装,生产不同种类服装需要租用不同设备,设备租金、生产成本、销售价格等指标如下表所示。
如果各类服装的市场需求都足够大,服装厂每月可用人工时为 2000h,那么应该如何安排生产计划使利润最大?
1.3、建模过程分析
首先要理解生产某种服装就会发生设备租金,租金只与是否生产该产品有关,而与生产数量无关,这就是固定成本。因此本题属于固定费用问题。
有些同学下意识地认为是从 3 种产品中选择一种,但题目中并没有限定必须或只能生产一种产品,因此决策结果可以是都不生产、选择 1 种或 2 种产品、3 种都生产。
决策结果会是什么都不生产吗?有可能的。
每种产品的利润:(销售价格 - 材料成本)× 生产数量 - 设备租金
本题中如果设备租金很高,决策结果就可能是什么都不做时利润最大,这是利润为 0,至少不亏。
现在可以用固定费用问题的数学模型来描述问题了:

1.4、PuLP 求解固定费用问题的编程
编程求解建立的数学模型,用标准模型的优化算法对模型求解,得到优化结果。
模型求解的编程步骤与之前的线性规划、整数规划问题并没有什么区别,这就是 PuLP工具包的优势。
(0)导入 PuLP库函数
import pulp
(1)定义一个规划问题
FixedCostP1 = pulp.LpProblem("Fixed_cost_problem", sense=pulp.LpMaximize) # 定义问题,求最大值
pulp.LpProblem 用来定义问题的构造函数。"FixedCostP1"是用户定义的问题名。
参数 sense 指定问题求目标函数的最小值/最大值 。本例求最大值,选择 “pulp.LpMaximize” 。
(2)定义决策变量
x1 = pulp.LpVariable('A', cat='Binary') # 定义 x1,0-1变量,是否生产 A 产品
x2 = pulp.LpVariable('B', cat='Binary') # 定义 x2,0-1变量,是否生产 B 产品
x3 = pulp.LpVariable('C', cat='Binary') # 定义 x3,0-1变量,是否生产 C 产品
y1 = pulp.LpVariable('yieldA', lowBound=0, upBound=100, cat='Integer') # 定义 y1,整型变量
y2 = pulp.LpVariable('yieldB', lowBound=0, upBound=600, cat='Integer') # 定义 y2,整型变量
y3 = pulp.LpVariable('youCans', lowBound=0, upBound=150, cat='Integer') # 定义 y3,整型变量
pulp.LpVariable 用来定义决策变量的函数。参数 cat 用来设定变量类型,' Binary ' 表示0/1变量(用于0/1规划问题),' Integer ' 表示整数变量。'lowBound'、'upBound' 分别表示变量取值范围的下限和上限。
(3)添加目标函数
FixedCostP1 += pulp.lpSum(-5000*x1-2000*x2-2000*x3+120*y1+10*y2+100*y3) # 设置目标函数 f(x)
(4)添加约束条件
FixedCostP1 += (5*y1 + y2 + 4*y3 <= 2000) # 不等式约束 FixedCostP1 += (3*y1 - 300*x1 <= 0) # 不等式约束 FixedCostP1 += (0.5*y2 - 300*x2 <= 0) # 不等式约束 FixedCostP1 += (2*y3 - 300*x3 <= 0) # 不等式约束
添加约束条件使用 "问题名 += 约束条件表达式" 格式。
约束条件可以是等式约束或不等式约束,不等式约束可以是 小于等于 或 大于等于,分别使用关键字">="、"<="和"=="。
(5)求解
FixedCostP1.solve()
solve() 是求解函数,可以对求解器、求解精度进行设置。
1.5、Python 例程:固定费用问题
import pulp # 导入 pulp 库
# 主程序
def main():
# 固定费用问题(Fixed cost problem)
print("固定费用问题(Fixed cost problem)")
# 问题建模:
"""
决策变量:
y(i) = 0, 不生产第 i 种产品
y(i) = 1, 生产第 i 种产品
x(i), 生产第 i 种产品的数量, i>=0 整数
i=1,2,3
目标函数:
min profit = 120x1 + 10x2+ 100x3 - 5000y1 - 2000y2 - 2000y3
约束条件:
5x1 + x2 + 4x3 <= 2000
3x1 <= 300y1
0.5x2 <= 300y2
2x3 <= 300y3
变量取值范围:Youcans XUPT
0<=x1<=100, 0<=x2<=600, 0<=x3<=150, 整数变量
y1, y2 ,y3 为 0/1 变量
"""
# 1. 固定费用问题(Fixed cost problem), 使用 PuLP 工具包求解
# (1) 建立优化问题 FixedCostP1: 求最大值(LpMaximize)
FixedCostP1 = pulp.LpProblem("Fixed_cost_problem_1", sense=pulp.LpMaximize) # 定义问题,求最大值
# (2) 建立变量
x1 = pulp.LpVariable('A', cat='Binary') # 定义 x1,0-1变量,是否生产 A 产品
x2 = pulp.LpVariable('B', cat='Binary') # 定义 x2,0-1变量,是否生产 B 产品
x3 = pulp.LpVariable('C', cat='Binary') # 定义 x3,0-1变量,是否生产 C 产品
y1 = pulp.LpVariable('yieldA', lowBound=0, upBound=100, cat='Integer') # 定义 y1,整型变量
y2 = pulp.LpVariable('yieldB', lowBound=0, upBound=600, cat='Integer') # 定义 y2,整型变量
y3 = pulp.LpVariable('yieldC', lowBound=0, upBound=150, cat='Integer') # 定义 y3,整型变量
# (3) 设置目标函数
FixedCostP1 += pulp.lpSum(-5000*x1-2000*x2-2000*x3+120*y1+10*y2+100*y3) # 设置目标函数 f(x)
# (4) 设置约束条件
FixedCostP1 += (5*y1 + y2 + 4*y3 <= 2000) # 不等式约束
FixedCostP1 += (3*y1 - 300*x1 <= 0) # 不等式约束
FixedCostP1 += (0.5*y2 - 300*x2 <= 0) # 不等式约束
FixedCostP1 += (2*y3 - 300*x3 <= 0) # 不等式约束
# (5) 求解 youcans
FixedCostP1.solve()
# (6) 打印结果
print(FixedCostP1.name)
if pulp.LpStatus[FixedCostP1.status] == "Optimal": # 获得最优解
for v in FixedCostP1.variables(): # youcans
print(v.name, "=", v.varValue) # 输出每个变量的最优值
print("Youcans F(x) = ", pulp.value(FixedCostP1.objective)) # 输出最优解的目标函数值
return
if __name__ == '__main__': # Copyright 2021 YouCans, XUPT
main()
1.6、Python 例程运行结果
Welcome to the CBC MILP Solver
Version: 2.9.0
Build Date: Feb 12 2015
Result - Optimal solution found
Fixed_cost_problem_1
A = 1.0
B = 1.0
C = 1.0
yieldA = 100.0
yieldB = 600.0
yieldC = 150.0
Max F(x) = 24000.0
从固定费用问题模型的求解结果可知,A、B、C 三种服装都生产,产量分别为 A/100、B/600、C/150 时获得最大利润为:24000。
二、PuLP 求解规划问题的快捷方法
2.1、PuLP 求解固定费用问题的编程
通过从线性规划、整数规划、0-1规划到上例中的混合0-1规划问题,我们已经充分体会到 PuLP 使用相同的步骤和参数处理不同问题所带来的便利。
但是,如果问题非常复杂,例如变量数量很多,约束条件复杂,逐个定义变量、逐项编写目标函数与约束条件的表达式,不仅显得重复冗长,不方便修改对变量和参数的定义,而且在输入过程中容易发生错误。因此,我们希望用字典、列表、循环等快捷方法来进行变量定义、目标函数和约束条件设置。
PuLP 提供了快捷建模的编程方案,下面我们仍以上节中的固定费用问题为例进行介绍。本例中的问题、条件和参数都与上节完全相同,以便读者进行对照比较快捷方法的具体内容。
(0)导入 PuLP 库函数
import pulp
(1)定义一个规划问题
FixedCostP2 = pulp.LpProblem("Fixed_cost_problem", sense=pulp.LpMaximize) # 定义问题,求最大值
(2)定义决策变量
types = ['A', 'B', 'C'] # 定义产品种类
status = pulp.LpVariable.dicts("生产决策", types, cat='Binary') # 定义 0/1 变量,是否生产该产品
yields = pulp.LpVariable.dicts("生产数量", types, lowBound=0, upBound=600, cat='Integer') # 定义整型变量
本例中的快捷方法使用列表 types 定义 0/1 变量 status 和 整型变量 yields,不论产品的品种有多少,都只有以上几句,从而使程序大为简化。
(3)添加目标函数
fixedCost = {'A':5000, 'B':2000, 'C':2000} # 各产品的 固定费用
unitProfit = {'A':120, 'B':10, 'C':100} # 各产品的 单位利润
FixedCostP2 += pulp.lpSum([(yields[i]*unitProfit[i]- status[i]*fixedCost[i]) for i in types])
虽然看起来本例中定义目标函数的程序语句较长,但由于使用字典定义参数、使用 for 循环定义目标函数,因此程序更加清晰、简明、便于修改参数、不容易输入错误。
(4)添加约束条件
humanHours = {'A':5, 'B':1, 'C':4} # 各产品的 单位人工工时
machineHours = {'A':3.0, 'B':0.5, 'C':2.0} # 各产品的 单位设备工时
maxHours = {'A':300, 'B':300, 'C':300} # 各产品的 最大设备工时
FixedCostP2 += pulp.lpSum([humanHours[i] * yields[i] for i in types]) <= 2000 # 不等式约束
for i in types:
FixedCostP2 += (yields[i]*machineHours[i] - status[i]*maxHours[i] <= 0) # 不等式约束
快捷方法对于约束条件的定义与对目标函数的定义相似,使用字典定义参数,使用循环定义约束条件,使程序简单、结构清楚。
注意本例使用了两种不同的循环表达方式:语句内使用 for 循环遍历列表实现所有变量的线性组合,标准的 for 循环结构实现多组具有相似结构的约束条件。读者可以对照数学模型及上例的例程,理解这两种定义约束条件的快捷方法。
(5)求解和结果的输出
# (5) 求解
FixedCostP2.solve()
# (6) 打印结果
print(FixedCostP2.name)
temple = "品种 %(type)s 的决策是:%(status)s,生产数量为:%(yields)d"
if pulp.LpStatus[FixedCostP2.status] == "Optimal": # 获得最优解
for i in types:
output = {'type': i,
'status': '同意' if status[i].varValue else '否决',
'yields': yields[i].varValue}
print(temple % output) # youcans@qq.com
print("最大利润 = ", pulp.value(FixedCostP2.objective)) # 输出最优解的目标函数值
由于快捷方法使用列表或字典定义变量,对求解的优化结果也便于实现结构化的输出。
2.2、Python 例程:PuLP 快捷方法
import pulp # 导入 pulp 库
# 主程序
def main():
# 2. 问题同上,PuLP 快捷方法示例
# (1) 建立优化问题 FixedCostP2: 求最大值(LpMaximize)
FixedCostP2 = pulp.LpProblem("Fixed_cost_problem_2", sense=pulp.LpMaximize) # 定义问题,求最大值
# (2) 建立变量
types = ['A', 'B', 'C'] # 定义产品种类
status = pulp.LpVariable.dicts("生产决策", types, cat='Binary') # 定义 0/1 变量,是否生产该产品
yields = pulp.LpVariable.dicts("生产数量", types, lowBound=0, upBound=600, cat='Integer') # 定义整型变量
# (3) 设置目标函数
fixedCost = {'A':5000, 'B':2000, 'C':2000} # 各产品的 固定费用
unitProfit = {'A':120, 'B':10, 'C':100} # 各产品的 单位利润
FixedCostP2 += pulp.lpSum([(yields[i]*unitProfit[i]- status[i]*fixedCost[i]) for i in types])
# (4) 设置约束条件
humanHours = {'A':5, 'B':1, 'C':4} # 各产品的 单位人工工时
machineHours = {'A':3.0, 'B':0.5, 'C':2.0} # 各产品的 单位设备工时
maxHours = {'A':300, 'B':300, 'C':300} # 各产品的 最大设备工时
FixedCostP2 += pulp.lpSum([humanHours[i] * yields[i] for i in types]) <= 2000 # 不等式约束
for i in types:
FixedCostP2 += (yields[i]*machineHours[i] - status[i]*maxHours[i] <= 0) # 不等式约束
# (5) 求解 youcans
FixedCostP2.solve()
# (6) 打印结果
print(FixedCostP2.name)
temple = "品种 %(type)s 的决策是:%(status)s,生产数量为:%(yields)d"
if pulp.LpStatus[FixedCostP2.status] == "Optimal": # 获得最优解
for i in types:
output = {'type': i,
'status': '同意' if status[i].varValue else '否决',
'yields': yields[i].varValue}
print(temple % output)
print("最大利润 = ", pulp.value(FixedCostP2.objective)) # 输出最优解的目标函数值
return
if __name__ == '__main__': # Copyright 2021 YouCans, XUPT
main()
2.3、Python 例程运行结果
Welcome to the CBC MILP Solver
Version: 2.9.0
Build Date: Feb 12 2015
Result - Optimal solution found
Fixed_cost_problem_2
品种 A 的决策是:同意,生产数量为:100
品种 B 的决策是:同意,生产数量为:600
品种 C 的决策是:同意,生产数量为:150
最大利润 = 24000.0
本例的问题、条件和参数都与上节完全相同,只是采用 PuLP 提供的快捷建模的编程方案,优化结果也与 PuLP 标准方法完全相同,但本例使用了结构化的输出显示,使输出结果更为直观。
以上就是浅谈Python数学建模之固定费用问题的详细内容,更多关于Python 数学建模 固定费用的资料请关注易盾网络其它相关文章!
