偶然翻滴滴官网看到首页下翻第六栏(大概)有个绚丽的地球的三维动画,试着用there.js实现了下,基本实现了动画效果,不过还是有些问题;这个动画看似简单,但也用到好的绘制方法和计算,这里先写一下主要功能的实现;
先看示例:http://39.106.166.212:8080/webgl/t4(由于是写dome的一个项目,内容较多没做优化,第一次加载会会比较慢,需多等待几秒)
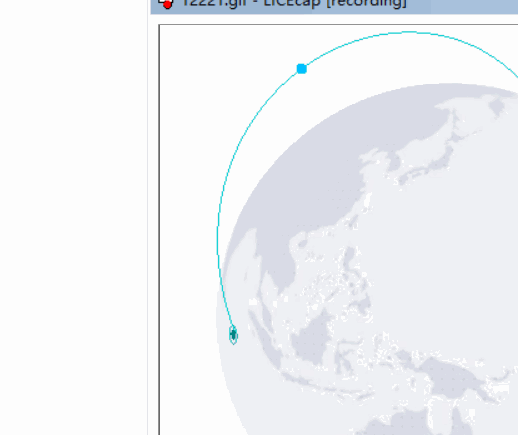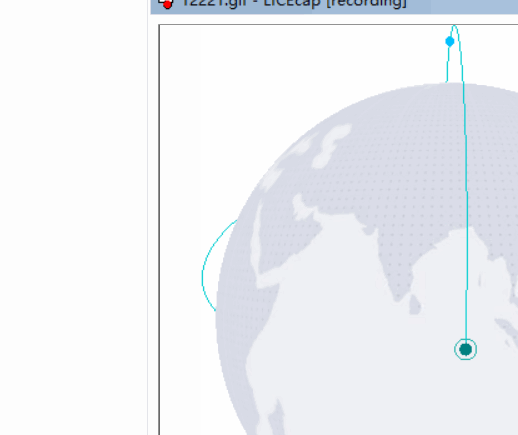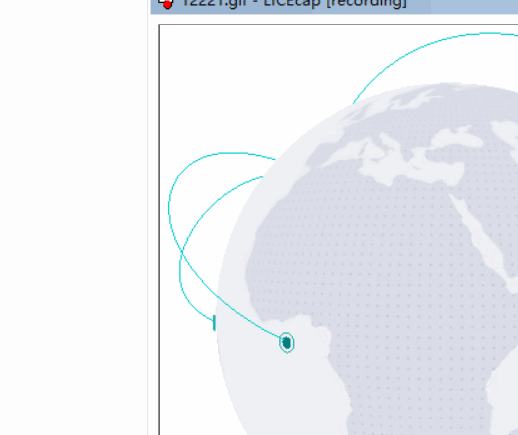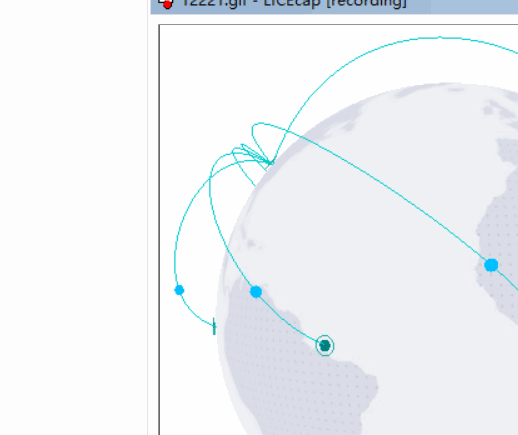
(lice这个截图工具也是很不好用,每次都截到一半 ╮(╯﹏╰)╭)
一、 3d绘制场景的构建
绘制一个3d程序首先需要添加 渲染器,场景,照相机 这些元素,这里补充一个灯光;
1、渲染器
首先创建一个渲染器,参数为页面中的canvas元素,
渲染器的作用就是把3d场景的内容结合照相机渲染到页面中,
最后将画布背景设为白色。
const renderer = new Three.WebGLRenderer({canvas: this.$refs.thr});
renderer.setClearColor(0x000000);
2、场景
场景顾名思义,就是添加一个你发挥(绘制)的场地,后面所有绘制的元素都要添加到场景中;
cosnt scene = new Three.Scene();
3、照相机
照相机就像人的视觉或说从什么角度去看场景,看场景的位置和视线的方向决定了渲染到页面的内容。故一般需要设置两个参数相机位置position、视线方向lookAt,,在webgl其实是需要三组参数视点,观察点,和上方向。thresjs中好像是默认Y轴为上方向了,这里使用透视相机。
const camera = new THREE.PerspectiveCamera(45, 500 / 500, 1, 1500); camera.position.set(100, 100, 1000); camera.lookAt(new THREE.Vector3(0, 0, 0)); scene.add(this.camera);
4、灯光
这里使用THREE.HemisphereLight光,可以更加贴近自然的户外光照效;
let light = new THREE.HemisphereLight(0xffffff); light.position.set(0, 0, 200); scene.add(light)
以上我们基本的绘制要素已添加完成,下面开始绘制各个几何体内容;
几何体的绘制有三部:创建几何体,创建材料,添加网格模型;
二、地球的绘制
threejs中提供了球体的绘制,我们只需创建一个球体,材料使用纹理贴图方式添加地图;
贴图图片资源是我从官网上找的
const geometry = new THREE.SphereGeometry(this.radius, 100, 100); // 球体
const textureLoader = new THREE.TextureLoader(); // 创建纹理贴图
const texture = textureLoader.load(require("@/assets/map.jpg"),texture => {
let material = new THREE.MeshLambertMaterial({map: texture,transparent: true,});
let mesh = new THREE.Mesh(geometry, material);
scene.add(mesh);
});
由于图片加载是异步的 ,这里需等图片加载完成后才能创建材质;
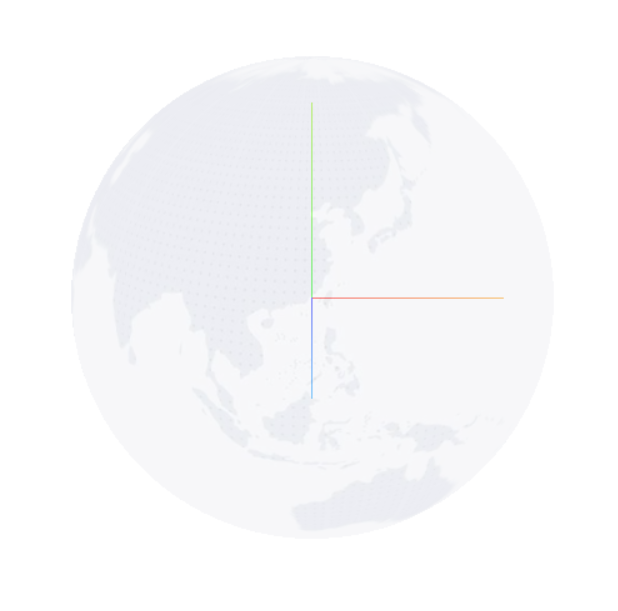
这里我们就创建好了一个地球模型,接着还要让其转动起来;(中间为xyz坐标轴)
threejs提供了几何体的基本3d变换,直接使用rotateY(angleChange)根据时间设置其绕y轴(绿色轴)旋转角度即可;
三、球面坐标点的绘制
1、在绘制球面位置点时,需先前先看下球坐标系,确定点的位置,webgl中坐标方向与下图不一致,但是对点的表示方法是一致的;
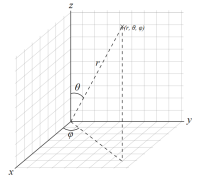
球面上任意点可以用r,θ,φ表示,也可通过以下公式转化到直角坐标系中
x=rsinθcosφ.
y=rsinθsinφ.
z=rcosθ
但实际中地球位置我们一般也会使用经纬度表示。。。 下面写个经纬度转坐标的方法。
threejs提供了THREE.Math.degToRad方法可以将经纬度转化为θ,φ,转化方法如下,这里为了方便后面使用,我直接返回一个3维向量;
getPosition(longitude, latitude, radius = this.radius) { // 经度,纬度转换为坐标
let lg = THREE.Math.degToRad(longitude);
let lt = THREE.Math.degToRad(latitude); // 获取x,y,z坐标
let temp = radius * Math.cos(lt);
let x = temp * Math.sin(lg);
let y = radius * Math.sin(lt);
let z = temp * Math.cos(lg);
return new THREE.Vector3(x, y, z);
}
2、知道了位置的表示方法后开始绘制表示位置的点
根据示例位置点的由点和一个圆环组成,我们先绘制一个二维平面内的点和圆弧,在通过设置其位置和旋转方式移动到目标坐标位置点;
(这里也可以绘制几何小球体来模拟)
(1)点的绘制
THREE.Shape是用来绘制二维平面内的形状的,设置其形状为圆弧,即可实现一个原点;
let shapePoint = new THREE.Shape();
shapePoint.absarc(0, 0, r - 4, 0, 2 * Math.PI, false);
let arcGeometry = new THREE.ShapeGeometry(shapePoint);
let arcMaterial = new THREE.MeshBasicMaterial({ color: 0x008080 });
let point = new THREE.Mesh(arcGeometry, arcMaterial);
(2)圆弧的绘制
let geometryLine = new THREE.Geometry();
let arc = new THREE.ArcCurve(0, 0, r, 0, 2 * Math.PI);
let points = arc.getPoints(40);
geometryLine.setFromPoints(points);
let LineMateri = new THREE.LineBasicMaterial({ color: 0x20b2aa });
let line = new THREE.Line(geometryLine, LineMateri);
(3)位置的设置
position.set(pos.x, pos.y, pos.z);
(4)二维图形旋转至球面
THREE.Spherical()方法 ,可将坐标点转化为坐标点转化回球坐标系的偏移角度;
let spherical = new THREE.Spherical(); spherical.setFromCartesianCoords(pos.x, pos.y, pos.z);
设置位置点旋转
Point.rotateX(spherical.phi - Math.PI / 2); Point.rotateY(spherical.theta);
这里为什么要 - Math.PI / 2 是因为开始我们绘制时,平面是垂直于y轴的平面,参考下面这幅图;
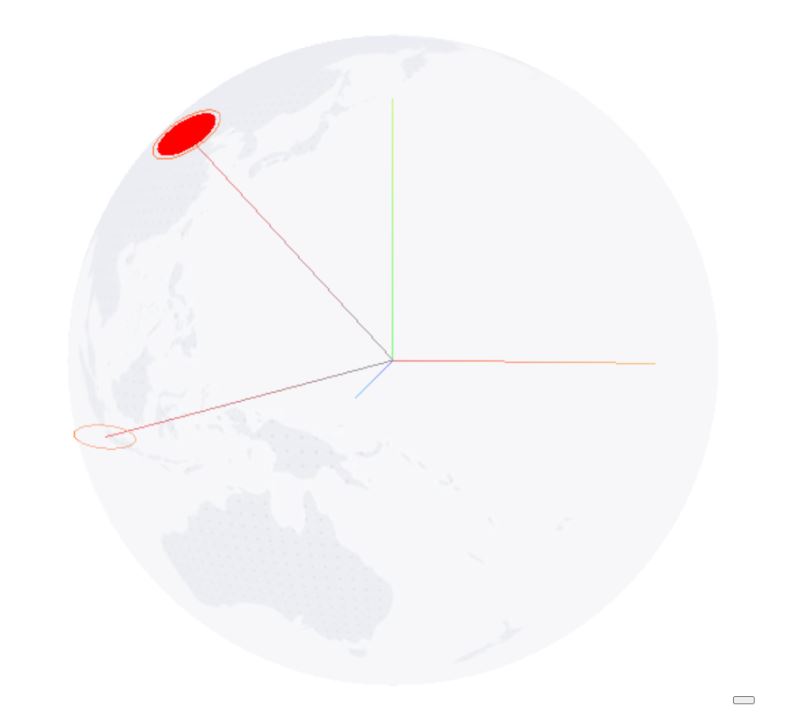
四、接着绘制链接球面两点间的连线
连接两点的曲线需在球面上方,
两点间可以坐出无数条曲线,那么如何确定曲线,我们需自己再选择合适的参数来确定;
首先想的是二阶贝塞尔曲线,取两点的中点为控制点,但如果链接两点刚好位于球面的两个对称端点(两点间连线为直径)时,控制点需在无穷远处;
故考虑使用三阶贝塞尔曲线,连接球面两点和球心,三点确定的一个平面如下图,
链接v1 v1,取中点c,链接oc,做一条射线,在射线取一点p,链接v1p,v2p,在v1,v2上取两点作为控制点;
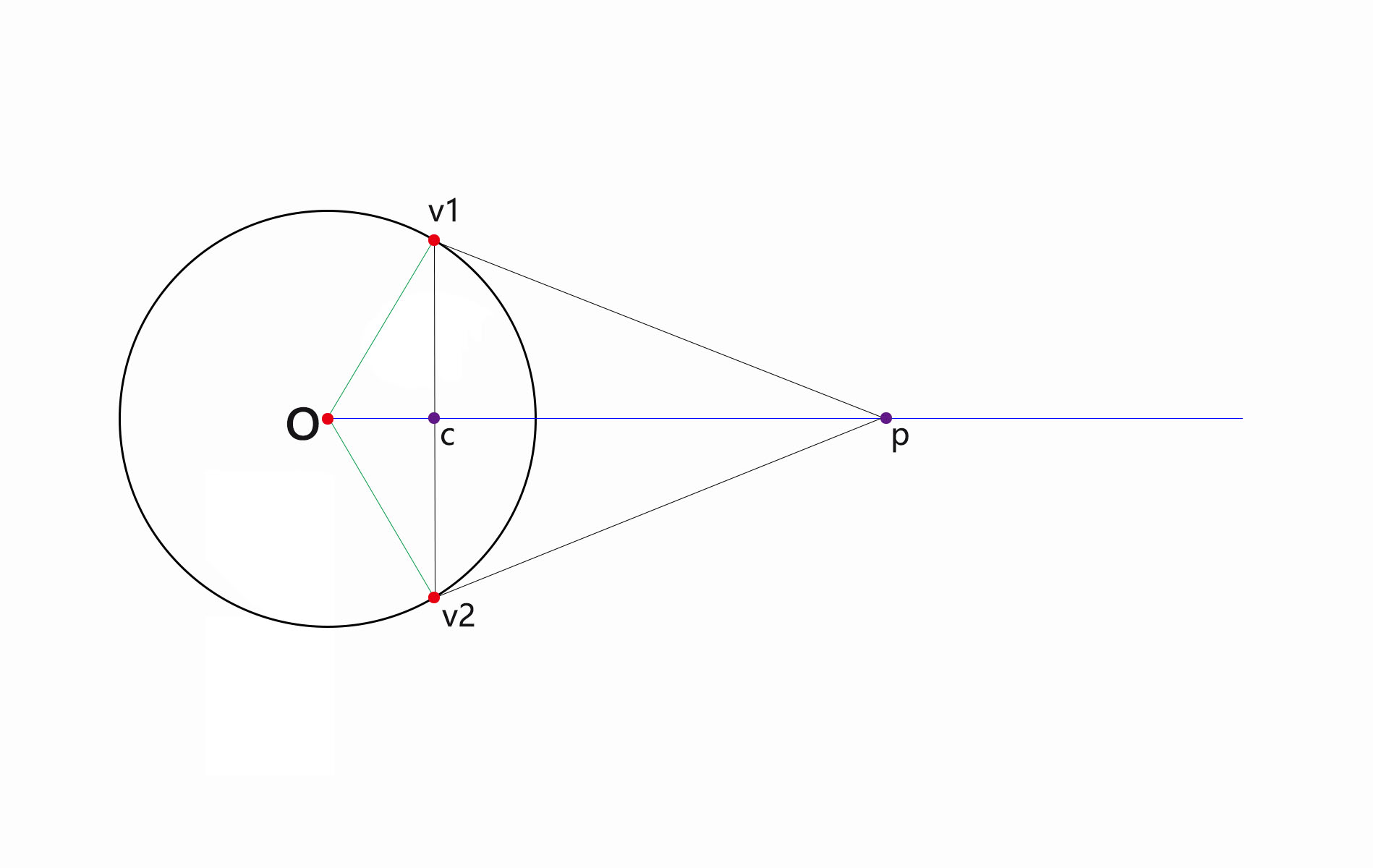
求两点的中点
getVCenter(v1, v2) {
let v = v1.add(v2);
return v.divideScalar(2);
}
获取两点间指定比例位置坐标
getLenVcetor(v1, v2, len) {
let v1v2Len = v1.distanceTo(v2);
return v1.lerp(v2, len / v1v2Len);
}
获取贝塞尔控制点
getBezierPoint(v0, v3) {
let angle = (v0.angleTo(v3) * 180) / Math.PI; // 0 ~ Math.PI // 计算向量夹角
let aLen = angle * 2.5,
hLen = angle * angle * 50;
let p0 = new THREE.Vector3(0, 0, 0); // 法线向量
let rayLine = new THREE.Ray(p0, this.getVCenter(v0.clone(), v3.clone())); // 顶点坐标
let vtop = rayLine.at(hLen / rayLine.at(1).distanceTo(p0), vtop); // 位置
// 控制点坐标
let v1 = this.getLenVcetor(v0.clone(), vtop, aLen);
let v2 = this.getLenVcetor(v3.clone(), vtop, aLen);
return {
v1: v1,
v2: v2
};
},
绘制三次贝塞尔曲线
drawLine(longitude, latitude, longitude2, latitude2) {
let geometry = new THREE.Geometry(); //声明一个几何体对象Geometry
let v0 = this.getPosition(longitude, latitude, this.radius);
let v3 = this.getPosition(longitude2, latitude2, this.radius);
let { v1, v2 } = this.getBezierPoint(v0, v3); // 三维二次贝赛尔曲线
let curve = new THREE.CubicBezierCurve3(v0, v1, v2, v3);
let curvePoints = curve.getPoints(100);
geometry.setFromPoints(curvePoints);
let material = new THREE.LineBasicMaterial({
color: 0xff7e41
});
let line = new THREE.Line(geometry, material);
this.group.add(line);
this.sport(curvePoints);
},
五、小球的运动轨迹
小球的动画我们使用three的帧动画,路径可以直接使用上一步中的曲线;
1、绘制小球
drawSportPoint(position, name) {
let box = new THREE.SphereGeometry(6, 6, 6);
let material = new THREE.MeshLambertMaterial({
color: 0x00bfff
}); //材质对象
let mesh = new THREE.Mesh(box, material);
mesh.name = name;
mesh.position.set(position.x, position.y, position.z);
this.groupBall.add(mesh);
this.group.add(this.groupBall);
return mesh;
}
2、让小球动起来
sport(curvePoints, index) {
const Ball = this.drawSportPoint(curvePoints[0]);
let arr = Array.from(Array(101), (v, k) => k); // 生成一个时间序列
let times = new Float32Array(arr);
let posArr = [];
curvePoints.forEach(elem => {
posArr.push(elem.x, elem.y, elem.z);
}); // 创建一个和时间序列相对应的位置坐标系列
let values = new Float32Array(posArr); // 创建一个帧动画的关键帧数据,曲线上的位置序列对应一个时间序列
let posTrack = new THREE.KeyframeTrack("Ball.position", times, values);
let duration = 101;
let clip = new THREE.AnimationClip("default", duration, [posTrack]);
this.mixer = new THREE.AnimationMixer(Ball);
let AnimationAction = this.mixer.clipAction(clip);
AnimationAction.timeScale = 20;
AnimationAction.play();
}
3、在requestAnimationFrame中添加触发动画
this.mixer.update(this.clock.getDelta());
到此这篇关于Threejs实现滴滴官网首页地球动画的文章就介绍到这了,更多相关Threejs滴滴官网首页地球动画内容请搜索易盾网络以前的文章或继续浏览下面的相关文章希望大家以后多多支持易盾网络!
