js图数据结构处理 迪杰斯特拉算法代码实例

这篇文章主要介绍了js图数据结构处理 迪杰斯特拉算法代码实例,文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下

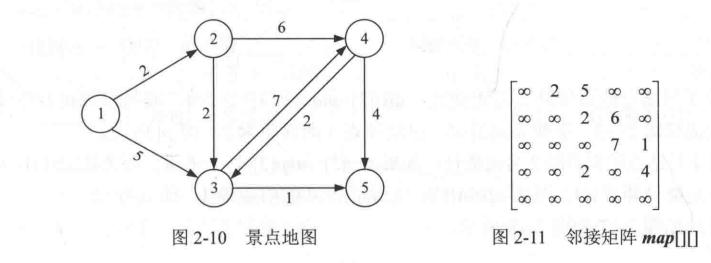
/*//1、确定数据结构, mapf[i][j] 为点i到点j的距离
    [
      Infinity  2     5  Infinity Infinity
      Infinity Infinity   2    6  Infinity
      Infinity Infinity Infinity   7    1
      Infinity Infinity   2  Infinity   4
      Infinity Infinity Infinity Infinity Infinity
    ];
     
     
    //2、如果源点为1，则 s = {1}, 则 v-s = {2,3,4,5}; s为已经规划好的点,v-s是需要规划的点 
    var dist = []; //dist[i] = mapf[1][i];dist[1] = 0;
    //源点1到i有边相连，初始化前驱为1（源点为前驱），否则初始化为-1
    var p = [-1,1,1,-1,-1];
     
     
    //3、找到 v-s = {2，3，4，5}集合里面,到源点1，最近的点
      //得出结果为2，节点为 t = 2，则 v-s={3、4、5}，s={1、2}；
       
    //4、借道t=2，所有t的相邻点，借道t；例如相邻点3,则 a = dist[2] + maf[2][3]; b = dist[3];
    //两个取较小值，得a < b; 2-3为捷径，则记录下dist[3] = a;记录下3的前驱点 p[3] = 2;
    //经过第4步，计算了2的相邻点，3、4；
     
    //5、比较v-s={3、4、5}的到源点的最近距离，即是 v-s={3、4、5}时，执行第3步，此时相当于源点为2会再次得出最小 t
     
    //6、重复 3、4、5步*/
     
     
     
    function Dijkstra(){
       //初始化构造一个集合，mapt[i][j]为点i到j的距离,不通的为无穷大
      var mapt = [
        [undefined,undefined,undefined,undefined,undefined,undefined],
        [undefined,Infinity,2,5,Infinity,Infinity],
        [undefined,Infinity,Infinity,2,6,Infinity],
        [undefined,Infinity,Infinity,Infinity,7,1],
        [undefined,Infinity,Infinity,2,Infinity,4],
        [undefined,Infinity,Infinity,Infinity,Infinity,Infinity],
      ];
       
      var n = mapt.length - 1;
      //开始计算
      this.dijkstra = function(u){ //u为源点
        var dist = []; //dist[i]为点i到y的最短距离
        var p = [];  //p[i] 为点i的前溯点
        var flag = []; //flag[i] 是否已经加入 s集合
       
        //初始化数据 dist,p,flag
        for(var i = 1; i <= n; i++){
          dist[i] = mapt[u][i]; //从源点到i的距离 
          if(dist[i] == Infinity){ //前溯点如果不通过为-1
            p[i] = -1;
          }else{
            p[i] = u;
          }
           
          flag[i] = false; //都没有选中
        }
         
        flag[u] = true; //选择了源点，s集合只有 u
 
        for(var i = 1; i <= n; i++){
          var t = u; var temp = Infinity;  
          for(var j = 1; j <= n ; j++){ //获取dist里面，v-s集合的最短距离
            if(!flag[j] && dist[j] <= temp){
              temp = dist[j];
              t = j;
            }
          }
           
          //查看是否找到最短的距离
          if(t == u){
            return {
              dist:dist,
              p:p
            }; 
          }
           
          //找到了,将t加入集合 s
          flag[t] = true;
           
          for(var k = 1 ; k <= n; k++){ //以t为捷径点(t为前溯点)，寻找所有满足条件的点
            if(!flag[k] && mapt[t][k] < Infinity ){
              if(dist[k] > (dist[t] + mapt[t][k])){
                dist[k] = dist[t] + mapt[t][k]; //源点到k的距离 > 源点到t的距离 + t到k的距离
                p[k] = t;
              }
            }
          }
        }
         
        return {
          dist:dist,
          p:p
        }
 
      }
       
      this.getpath = function(u){
        var process = this.dijkstra(u);
        var dist = process.dist;
        var p = process.p;
        for(var i = 1; i <= n; i++){
          var start = i;
          var str = i;
          while(start != -1){
            start = p[start]; //迭代出路径
            if(start != -1){
              str = str + '、' + start;
            }
          }
          console.log(str);
        }
      }
       
    }     
    var Dijk = new Dijkstra();
    //console.log(Dijk.dijkstra(1));
    console.log(Dijk.getpath(1));

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持易盾网络。