什么是回溯法
回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
无重复元素全排列问题
给定一个所有元素都不同的list,要求返回list元素的全排列。
设n = len(list),那么这个问题可以考虑为n叉树,对这个树进行dfs,这个问题里的回溯点就是深度(也就是templist的长度)为n时,回溯的条件就是当前元素已经出现在templist中了。
回溯法与递归:
回溯法是一种思想,递归是一种形式
class Solution(object):
#rtlist用来存储所有的返回所有排列,templist用来生成每个排列
def backtrack(self,rtlist,templist,nums):
if(len(templist) == len(nums)):
rtlist.append(templist[:])
else:
for i in nums:
if(i in templist): #如果在当前排列中已经有i了,就continue,相当于分支限界,即不对当前节点子树搜寻了
continue
templist.append(i)
self.backtrack(rtlist,templist,nums)
templist.pop() #把结尾的元素用nums中的下一个值替换掉,遍历下一颗子树
def permute(self,nums):
rtlist = []
templist = []
self.backtrack(rtlist,templist,nums)
return rtlist
nums=[1,2,3]时的树结构:
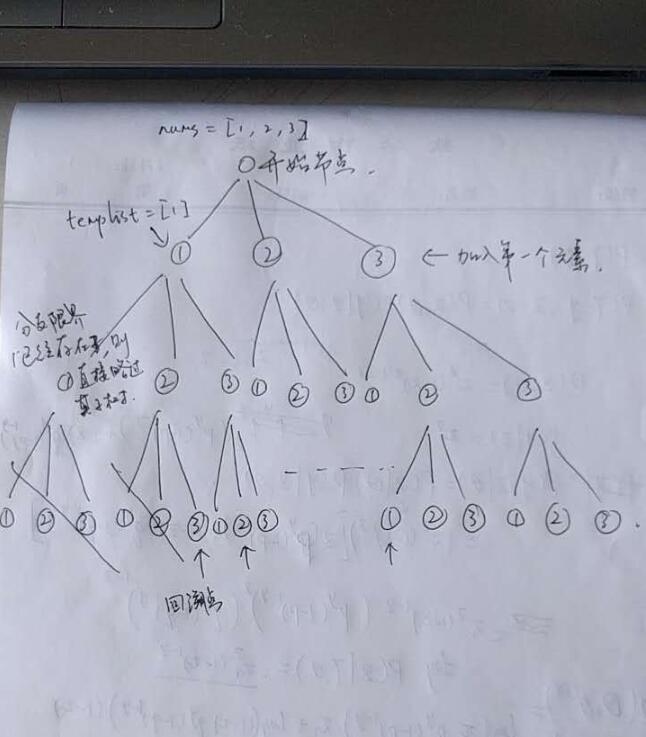
关键的就是确定好分支限界以及回溯点。
这里面有一个问题就是每次递归时把新加入的元素从nums删除在递归可不可以,实际上这样的时间复杂度并不会减少太多,因为对list进行操作还需要一定的时间,而原解法中因为有分支限界所以时间复杂度也不会太差。
有重复元素全排列
这个问题和上面的区别主要在于分支限界的差别,不能在使用出现重复元素作为回溯条件了,否则所有的都不满足。
这里我们应该使用计数器记录nums中每个元素出现的次数,如果当前元素超过次数则返回,但是这里还有一个问题就是可能会出现同样的排列多次,这里的解决办法就是同一层不许出现重复元素,这里有两种解决办法,一种是直接传入distinct的数组,还有一种是使用一个集合记录当前层已使用的元素。
第一种方法:
from collections import Counter
class Solution(object):
def backtrack(self, rtlist, tmplist, counter, nums, length):
if len(tmplist) == length:#回溯点
rtlist.append(tmplist[:])
else:
for i in nums:#横向遍历
if counter[i] == 0:#分支限界
continue
counter[i] -= 1
tmplist.append(i)
self.backtrack(rtlist, tmplist, counter, nums, length)#纵向遍历
counter[i] += 1
tmplist.pop()
def permuteUnique(self, nums):
rtlist, tmplist, counter = [], [], Counter(nums)
length = len(nums)
self.backtrack(rtlist, tmplist, counter, list(set(nums)), length)
return rtlist
第二种
from collections import Counter
class Solution(object):
def backtrack(self, rtlist, tmplist, level, counter, nums):
if len(tmplist) == len(nums):
rtlist.append(tmplist[:])
else:
for i in nums:
if i in level or counter[i] == 0:
continue
counter[i] -= 1
tmplist.append(i)
level.add(i)
self.backtrack(rtlist, tmplist, set(), counter, nums)
counter[i] += 1
tmplist.pop()
def permuteUnique(self, nums):
if not nums:
return []
rtlist, tmplist, level, counter = [], [], set(), Counter(nums)
self.backtrack(rtlist, tmplist, level, counter, nums)
return rtlist
在递归时不能用“=”修改父函数的变量,因为“=”只能改变变量的指向,要修改父函数的变量要直接在内存中修改,例如放入容器中可以直接找到变量内存地址。通常使用container.method()。
例如在上面的程序中如果我们想要在回溯点把counter复原不能使用counter = Counter(nums),而是应该逐个修改counter[key]
总结
回溯法其实就是把原问题考虑成一棵树,我们遍历这棵树在不可能的地方返回,不在遍历这个节点的子树,在满足要求时返回。
所以在回溯法中,关键的就是找出合理的分支限界(重要),和返回条件。
更多请参考
多叉树的遍历方法:
def travel(root):
遍历root
for subtree_root in 当前层所有节点:
travel(subtree_root)
在for中对一层的所有节点都执行了travel,又因为对所有节点的所有子树都执行了travel,所以可以完成遍历。
以上这篇python 回溯法模板详解就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持易盾网络。
