python计算波峰波谷值的方法（极值点）

python求极值点主要用到scipy库。

1. 首先可先选择一个函数或者拟合一个函数，这里选择拟合数据：np.polyfit

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy import signal #滤波等

xxx = np.arange(0, 1000)
yyy = np.sin(xxx*np.pi/180)

z1 = np.polyfit(xxx, yyy, 7) # 用7次多项式拟合
p1 = np.poly1d(z1) #多项式系数
print(p1) # 在屏幕上打印拟合多项式
yvals=p1(xxx) 

plt.plot(xxx, yyy, '*',label='original values')
plt.plot(xxx, yvals, 'r',label='polyfit values')
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.legend(loc=4)
plt.title('polyfitting')
plt.show()

得到的图形是：

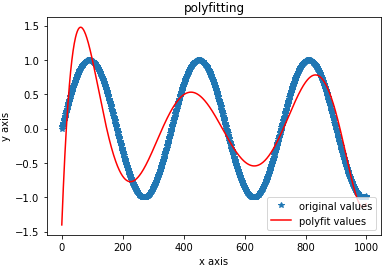
2. 求波峰值，也就是极大值，得到：signal.find_peaks

# 极值
num_peak_3 = signal.find_peaks(yvals, distance=10) #distance表极大值点的距离至少大于等于10个水平单位
print(num_peak_3[0])
print('the number of peaks is ' + str(len(num_peak_3[0])))
plt.plot(xxx, yyy, '*',label='original values')
plt.plot(xxx, yvals, 'r',label='polyfit values')
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.legend(loc=4)
plt.title('polyfitting')
for ii in range(len(num_peak_3[0])):
 plt.plot(num_peak_3[0][ii], yvals[num_peak_3[0][ii]],'*',markersize=10)
plt.show()

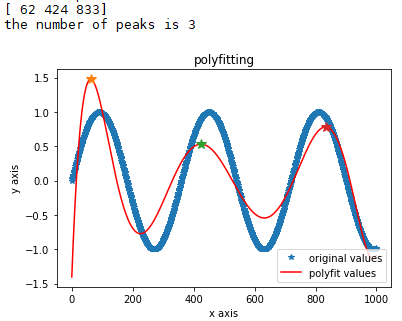
3. 在可导的情形下，可以求导来求极值点，同时得到极大值和极小值点：np.polyder

yyyd = np.polyder(p1,1) # 1表示一阶导
print(yyyd)

此时：yyyd.r 即可就得导数为0的点，可以与上述的极大值点对应比较

4. 直接函数分别求极大值和极小值：signal.argrelextrema 函数

print(yvals[signal.argrelextrema(yvals, np.greater)]) #极大值的y轴, yvals为要求极值的序列
print(signal.argrelextrema(yvals, np.greater)) #极大值的x轴
peak_ind = signal.argrelextrema(yvals,np.greater)[0] #极大值点，改为np.less即可得到极小值点
plt.plot(xxx, yyy, '*',label='original values')
plt.plot(xxx, yvals, 'r',label='polyfit values')
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.legend(loc=4)
plt.title('polyfitting')
plt.plot(signal.argrelextrema(yvals,np.greater)[0],yvals[signal.argrelextrema(yvals, np.greater)],'o', markersize=10) #极大值点
plt.plot(signal.argrelextrema(yvals,np.less)[0],yvals[signal.argrelextrema(yvals, np.less)],'+', markersize=10) #极小值点
plt.show()

总结

以上所述是小编给大家介绍的python计算波峰波谷值的方法（极值点），希望对大家有所帮助，也非常感谢大家对易盾网络网站的支持！