pytorch 模拟关系拟合——回归实例

本次用 pytroch 来实现一个简单的回归分析，也借此机会来熟悉 pytorch 的一些基本操作。

1. 建立数据集

import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt

# torch.linspace(-1,1,100)表示返回一个一维张量，包含在区间 -1到1 上均匀间隔的100个点；
# torch.unsqueeze(input,dim=1)表示转换维度
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
# 生成的y值为x的平方加上随机数 
y = x.pow(2) + 0.2*torch.rand(x.size())         

# 用 Variable 来修饰这些数据 tensor
x, y = torch.autograd.Variable(x), Variable(y)

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

2. 构建神经网络

import torch
import torch.nn.functional as F   # 激励函数都在这

class Net(torch.nn.Module): # 继承 torch 的 Module
  def __init__(self, n_feature, n_hidden, n_output):
    super(Net, self).__init__()   # 继承 __init__ 功能
    # 定义每层用什么样的形式
    self.hidden = torch.nn.Linear(n_feature, n_hidden)  # 隐藏层线性输出
    self.predict = torch.nn.Linear(n_hidden, n_output)  # 输出层线性输出

  def forward(self, x):  # 这同时也是 Module 中的 forward 功能
    # 正向传播输入值, 神经网络分析出输出值
    x = F.relu(self.hidden(x))   # 激励函数(隐藏层的线性值)
    x = self.predict(x)       # 输出值
    return x

net = Net(n_feature=1, n_hidden=10, n_output=1)

print(net) # net 的结构
"""
Net (
 (hidden): Linear (1 -> 10)
 (predict): Linear (10 -> 1)
)
"""

3. 实时绘图查看回归效果

import matplotlib.pyplot as plt

plt.ion() #打开交互绘图模式（便于实时显示图像变化）
plt.show() 

optimizer = torch.optim.SGD(net.parameters(), lr=0.1) # 定义优化器和学习率
loss_func = torch.nn.MSELoss() #定义损失函数

for t in range(200):
  prediction = net(x)
  loss = loss_func(prediction, y)

  optimizer.zero_grad()
  loss.backward()
  optimizer.step()

  if t%5 == 0:
    plt.cla() 
    plt.scatter(x.data.numpy(), y.data.numpy()) # 画散点图
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5) # 画拟合曲线
    plt.text(0.5, 0, 'Loss=%.4f' % loss.data[0], fontdict={'size':20,'color':'red'}) # 显示损失数值
    plt.pause(0.1)

# 如果在脚本中使用ion()命令开启了交互模式，没有使用ioff()关闭的话，则图像会一闪而过，并不会常留。要想防止这种情况，需要在plt.show()之前加上ioff()命令。
plt.ioff() 
plt.show()

运行终态效果图如下：

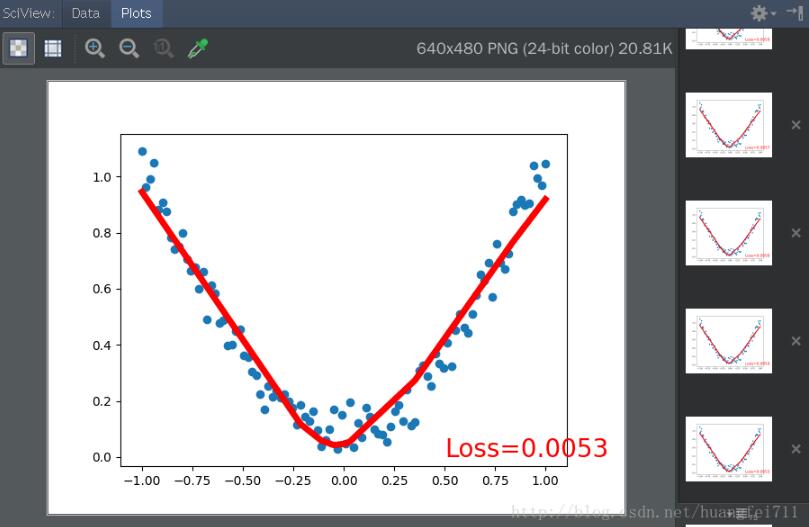
以上这篇pytorch 模拟关系拟合——回归实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持易盾网络。