我们知道,数据之间的关系有 3 种,分别是 一对一、一对多 和 多对多,前两种关系的数据可分别用线性表和树结构存储,本节学习存储具有多对多逻辑关系数据的结构 图 存储结构。
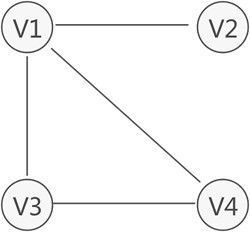
图 1 图存储结构示意图
图 1 所示为存储 V1、V2、V3、V4 的图结构,从图中可以清楚的看出数据之间具有的"多对多"关系。例如,V1 与 V4 和 V2 建立着联系,V4 与 V1 和 V3 建立着联系,以此类推。
与链表不同,图中存储的各个数据元素被称为顶点(而不是节点)。拿图 1 来说,该图中含有 4 个顶点,分别为顶点 V1、V2、V3 和 V4。
图存储结构中,习惯上用 Vi 表示图中的顶点,且所有顶点构成的集合通常用 V 表示,如图 1 中顶点的集合为 V={V1,V2,V3,V4}。
注意,图 1 中的图仅是图存储结构的其中一种,数据之间 "多对多" 的关系还可能用如图 2 所示的图结构表示:
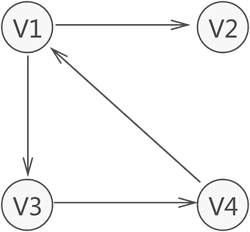
图 2 有向图示意图
可以看到,各个顶点之间的关系并不是"双向"的。比如,V4 只与 V1 存在联系(从 V4 可直接找到 V1),而与 V3 没有直接联系;同样,V3 只与 V4 存在联系(从 V3 可直接找到 V4),而与 V1 没有直接联系,以此类推。
因此,图存储结构可细分两种表现类型,分别为无向图(图 1)和有向图(图 2)。
图存储结构基本常识
弧头和弧尾
有向图中,无箭头一端的顶点通常被称为"初始点"或"弧尾",箭头直线的顶点被称为"终端点"或"弧头"。入度和出度
对于有向图中的一个顶点 V 来说,箭头指向 V 的弧的数量为 V 的入度(InDegree,记为 ID(V));箭头远离 V 的弧的数量为 V 的出度(OutDegree,记为OD(V))。拿图 2 中的顶点 V1来说,该顶点的入度为 1,出度为 2(该顶点的度为 3)。(V1,V2) 和 <V1,V2> 的区别
无向图中描述两顶点(V1 和 V2)之间的关系可以用 (V1,V2) 来表示,而有向图中描述从 V1 到 V2 的"单向"关系用 <V1,V2> 来表示。由于图存储结构中顶点之间的关系是用线来表示的,因此 (V1,V2) 还可以用来表示无向图中连接 V1 和 V2 的线,又称为边;同样,<V1,V2> 也可用来表示有向图中从 V1 到 V2 带方向的线,又称为弧。
集合 VR 的含义
并且,图中习惯用 VR 表示图中所有顶点之间关系的集合。例如,图 1 中无向图的集合 VR={(v1,v2),(v1,v4),(v1,v3),(v3,v4)},图 2 中有向图的集合 VR={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}。路径和回路
无论是无向图还是有向图,从一个顶点到另一顶点途径的所有顶点组成的序列(包含这两个顶点),称为一条路径。如果路径中第一个顶点和最后一个顶点相同,则此路径称为"回路"(或"环")。并且,若路径中各顶点都不重复,此路径又被称为"简单路径";同样,若回路中的顶点互不重复,此回路被称为"简单回路"(或简单环)。
拿图 1 来说,从 V1 存在一条路径还可以回到 V1,此路径为 {V1,V3,V4,V1},这是一个回路(环),而且还是一个简单回路(简单环)。
在有向图中,每条路径或回路都是有方向的。
权和网的含义
在某些实际场景中,图中的每条边(或弧)会赋予一个实数来表示一定的含义,这种与边(或弧)相匹配的实数被称为"权",而带权的图通常称为网。如图 3 所示,就是一个网结构: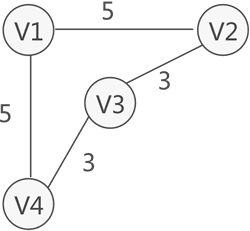
图 3 带权的图存储结构
子图:指的是由图中一部分顶点和边构成的图,称为原图的子图。
图存储结构的分类
根据不同的特征,图又可分为完全图,连通图、稀疏图和稠密图:-
完全图:若图中各个顶点都与除自身外的其他顶点有关系,这样的无向图称为完全图(如图 4a))。同时,满足此条件的有向图则称为有向完全图(图 4b))。
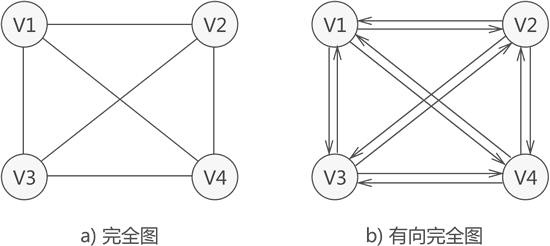
图 4 完全图示意图具有 n 个顶点的完全图,图中边的数量为 n(n-1)/2;而对于具有 n 个顶点的有向完全图,图中弧的数量为 n(n-1)。
-
稀疏图和稠密图:这两种图是相对存在的,即如果图中具有很少的边(或弧),此图就称为"稀疏图";反之,则称此图为"稠密图"。
稀疏和稠密的判断条件是:e<nlogn,其中 e 表示图中边(或弧)的数量,n 表示图中顶点的数量。如果式子成立,则为稀疏图;反之为稠密图。
有关连通图的相关知识,后续专门有一篇文章做详细介绍。
