使用python画出逻辑斯蒂映射(logistic map)中的分叉图

逻辑斯蒂映射在混沌数学中是一个很经典的例子，它可以说明混沌可以从很简单的非线性方程中产生。

逻辑斯蒂映射公式如下：

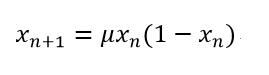
x_n表示当前人口与最大人口数量的比值，mu为参数，相当于人口增长速率。

分叉图描绘的是不同mu情况下，x收敛的值的分布图。

参考地址

python代码如下：

from tqdm import tqdm
import matplotlib.pyplot as plt
import numpy as np
def LogisticMap():
 mu = np.arange(2, 4, 0.0001)
 x = 0.2 # 初值
 iters = 1000 # 不进行输出的迭代次数
 last = 100 # 最后画出结果的迭代次数
 for i in tqdm(range(iters+last)):
  x = mu * x * (1 - x)
  if i >= iters:
   plt.plot(mu, x, ',k', alpha=0.25) # alpha设置透明度
 plt.show()
LogisticMap()

结果图：

补充知识：用Python画Logistic函数图像

我就废话不多说了，大家还是直接看代码吧~

import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0,1,0.01)
y = ln(x/(1-x))
plt.plot(y,x)

以上这篇使用python画出逻辑斯蒂映射(logistic map)中的分叉图案例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持易盾网络。