TensorFlow 支持自动求导,可以使用 TensorFlow 优化器来计算和使用梯度。它使用梯度自动更新用变量定义的张量。本节将使用 TensorFlow 优化器来训练网络。 前面章节中,我们定义了层、权
前面章节中,我们定义了层、权重、损失、梯度以及通过梯度更新权重。用公式实现可以帮助我们更好地理解,但随着网络层数的增加,这可能非常麻烦。
本节将使用 TensorFlow 的一些强大功能,如 Contrib(层)来定义神经网络层及使用 TensorFlow 自带的优化器来计算和使用梯度。
通过前面的学习,我们已经知道如何使用 TensorFlow 的优化器。Contrib 可以用来添加各种层到神经网络模型,如添加构建块。这里使用的一个方法是 tf.contrib.layers.fully_connected,在 TensorFlow 文档中定义如下:

这样就添加了一个全连接层。
提示:上面那段代码创建了一个称为权重的变量,表示全连接的权重矩阵,该矩阵与输入相乘产生隐藏层单元的张量。如果提供了 normalizer_fn(比如batch_norm),那么就会归一化。否则,如果 normalizer_fn 是 None,并且设置了 biases_initializer,则会创建一个偏置变量并将其添加到隐藏层单元中。最后,如果 activation_fn 不是 None,它也会被应用到隐藏层单元。
具体做法
第一步是改变损失函数,尽管对于分类任务,最好使用交叉熵损失函数。这里继续使用均方误差(MSE):
接下来,使用 GradientDescentOptimizer:

对于同一组超参数,只有这两处改变,在测试数据集上的准确率只有 61.3%。增加 max_epoch,可以提高准确性,但不能有效地发挥 TensorFlow 的能力。
这是一个分类问题,所以最好使用交叉熵损失,隐藏层使用 ReLU 激活函数,输出层使用 softmax 函数。做些必要的修改,完整代码如下所示:

解读分析
修改后的 MNIST MLP 分类器在测试数据集上只用了一个隐藏层,并且在 10 个 epoch 内,只需要几行代码,就可以得到 96% 的精度: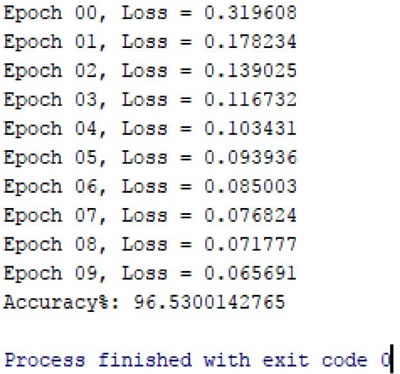
由此可见 TensorFlow 的强大之处。
