中序遍历的遍历方法为:对于当前结点,首先遍历左子树,然后访问当前节点,最后遍历右子树。中序遍历是二叉树遍历的一种,也叫做中根遍历、中序周游。

本教程操作环境:windows7系统、C++17版本、Dell G3电脑。
二叉树是一种重要的数据结构,对二叉树的遍历也很重要。这里简单介绍三种二叉树中序遍历的方法。二叉树的中序遍历就是首先遍历左子树,然后访问当前节点,最后遍历右子树。对于下面的二叉树,中序遍历结果如下:
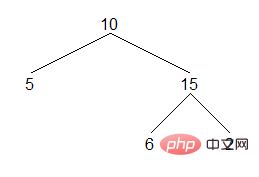
结果:[5,10,6,15,2]
直观来看,二叉树的中序遍历就是将节点投影到一条水平的坐标上。如图:
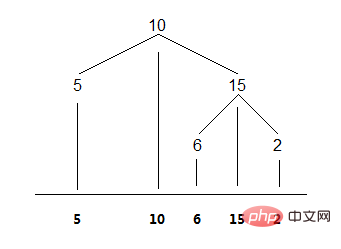
1、递归法
这是思路最简单的方法,容易想到并且容易实现。递归的终止条件是当前节点是否为空。首先递归调用遍历左子树,然后访问当前节点,最后递归调用右子树。代码如下:
//recursive
class Solution1 {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
if(root==NULL)return ret;
inorderHelper(ret,root);
return ret;
}
private:
void inorderHelper(vector<int>& ret,TreeNode* root)
{
if(root==NULL)return;
inorderHelper(ret,root->left);
ret.push_back(root->val);
inorderHelper(ret,root->right);
}
};2、迭代法
在迭代方法中,从根节点开始找二叉树的最左节点,将走过的节点保存在一个栈中,找到最左节点后访问,对于每个节点来说,它都是以自己为根的子树的根节点,访问完之后就可以转到右儿子上了。代码如下:
//iterate,using a stack
class Solution2 {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
if(root==NULL)return ret;
TreeNode *curr=root;
stack<TreeNode*> st;
while(!st.empty()||curr!=NULL)
{
while(curr!=NULL)
{
st.push(curr);
curr=curr->left;
}
curr=st.top();
st.pop();
ret.push_back(curr->val);
curr=curr->right;
}
return ret;
}
};这种方法时间复杂度是O(n),空间复杂度也是O(n)。
3、Morris法
这种方法是Morris发明的,看完之后感觉精妙无比。这种方法不使用递归,不使用栈,O(1)的空间复杂度完成二叉树的遍历。这种方法的基本思路就是将所有右儿子为NULL的节点的右儿子指向后继节点(对于右儿子不为空的节点,右儿子就是接下来要访问的节点)。这样,对于任意一个节点,当访问完它后,它的右儿子已经指向了下一个该访问的节点。对于最右节点,不需要进行这样的操作。注意,这样的操作是在遍历的时候完成的,完成访问节点后会把树还原。整个循环的判断条件为当前节点是否为空。例如上面的二叉树,遍历过程如下(根据当前节点c的位置):
(1)当前节点为10,因为左儿子非空,不能访问,找到c的左子树的最右节点p:
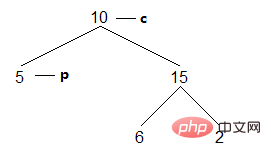
结果:[]
(2)找节点c的左子树的最右节点有两种终止条件,一种右儿子为空,一种右儿子指向当前节点。下面是右儿子为空的情况,这种情况先要构造,将节点p的右儿子指向后继节点c,然后c下移:
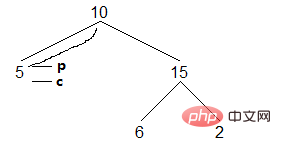
结果:[]
(3)当前节点c的左儿子为空,进行访问。访问后将c指向右儿子(即后继节点):
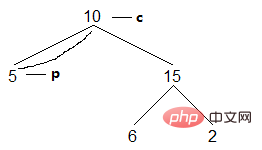
结果:[5]
(4)继续寻找左子树的最右节点,这次的终止条件是最右节点为当前节点。这说明当前节点的左子树遍历完毕,访问当前节点后,还原二叉树,将当前节点指向后继节点:
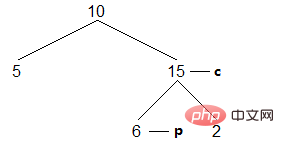
结果:[5,10]
(5)重复上述过程,直到c指向整棵二叉树的最右节点:
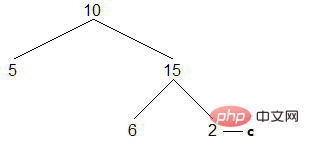
左儿子为空,进行访问,c转到右儿子。右儿子为空,不满足判断条件,循环结束,遍历完成。结果如下:
[5,10,6,15,2]
这就是Morris方法,时间复杂度为O(n),空间复杂度是O(1)。代码如下:
//Morris traversal,without a stack
class Solution3 {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
if(root==NULL)return ret;
TreeNode *curr=root;
TreeNode *pre;
while(curr)
{
if(curr->left==NULL)
{
ret.push_back(curr->val);
curr=curr->right;
}
else
{
pre=curr->left;
while(pre->right&&pre->right!=curr)
pre=pre->right;
if(pre->right==NULL)
{
pre->right=curr;
curr=curr->left;
}
else
{
ret.push_back(curr->val);
pre->right=NULL;
curr=curr->right;
}
}
}
return ret;
}
};
