目录 快速排序 完整代码: 直接选择排序 完整代码: 堆排序 完整代码: 总结 快速排序 简单解释:快速排序就是每次找一个基点(第一个元素),然后两个哨兵,一个从最前面往后走
目录
- 快速排序
- 完整代码:
- 直接选择排序
- 完整代码:
- 堆排序
- 完整代码:
- 总结
快速排序
简单解释: 快速排序就是每次找一个基点(第一个元素),然后两个哨兵,一个从最前面往后走,一个从最后面往前面走,如果后面那个哨兵找到了一个比基点大的数停下来,前面那个哨兵找到比基点大的数停下来,然后交换两个哨兵找到的数,如果找不到最后两个哨兵就会碰到一起就结束,最后交换基点和哨兵相遇的地方的元素,然后就将一个序列分为比基点小的一部分和比基点大的一部分,然后递归左半部分和右半部分,最后的结果就是有序的了。
完整代码:
package com.keafmd.Sequence;
/**
* Keafmd
*
* @ClassName: QuickSort
* @Description: 快速排序
* @author: 牛哄哄的柯南
* @date: 2021-06-24 10:32
*/
public class QuickSort {
//快速排序
public static void quickSort(int[] arr) {
quickSort(arr, true);
}
public static void quickSort(int[] arr, boolean ascending) {
if (ascending) {
quickSort(arr, 0, arr.length - 1, true);
} else {
quickSort(arr, 0, arr.length - 1, false);
}
}
public static void quickSort(int[] arr, int begin, int end, boolean ascending) {
if (ascending)
quickSort(arr, begin, end);
else
quickSortDescending(arr, begin, end);
}
//快排序升序 -- 默认
public static void quickSort(int[] arr, int begin, int end) {
if (begin > end) { //结束条件
return;
}
int base = arr[begin];
int i = begin, j = end;
while (i < j) { // 两个哨兵(i左边,j右边)没有相遇
while (arr[j] >= base && i < j) { //哨兵j没找到比base小的
j--;
}
while (arr[i] <= base && i < j) { //哨兵i没找到比base大的
i++;
}
if (i < j) { //如果满足条件则交换
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//最后将基准为与i和j相等位置的数字交换
arr[begin] = arr[i];
arr[i] = base;
quickSort(arr, begin, i - 1); //递归调用左半数组
quickSort(arr, i + 1, end); //递归调用右半数组
}
//快排序降序
public static void quickSortDescending(int[] arr, int begin, int end) {
if (begin > end) { //结束条件
return;
}
int base = arr[begin];
int i = begin, j = end;
while (i < j) { // 两个哨兵(i左边,j右边)没有相遇
while (arr[j] <= base && i < j) { //哨兵j没找到比base大的
j--;
}
while (arr[i] >= base && i < j) { //哨兵i没找到比base小的
i++;
}
if (i < j) { //如果满足条件则交换
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//最后将基准为与i和j相等位置的数字交换
arr[begin] = arr[i];
arr[i] = base;
quickSortDescending(arr, begin, i - 1); //递归调用左半数组
quickSortDescending(arr, i + 1, end); //递归调用右半数组
}
}
直接选择排序
简单解释: 数组分为已排序部分(前面)和待排序序列(后面) 第一次肯定所有的数都是待排序的 从待排序的序列中找到最大或最小的那个元素,放到前面的已排序部分,然后一直找,不断缩小待排序的范围,直到所有的数都是已排序的了
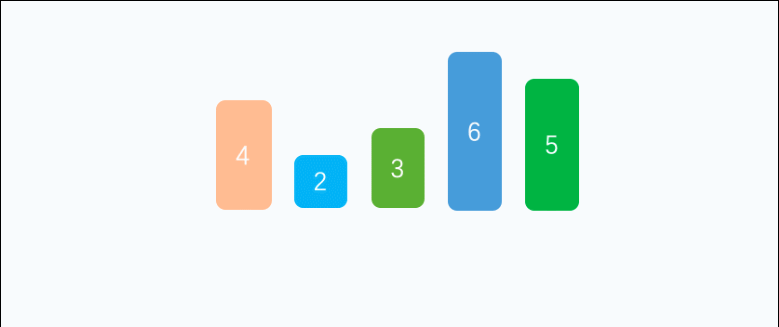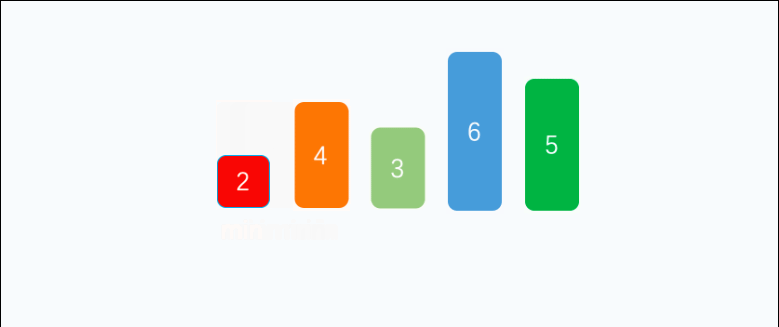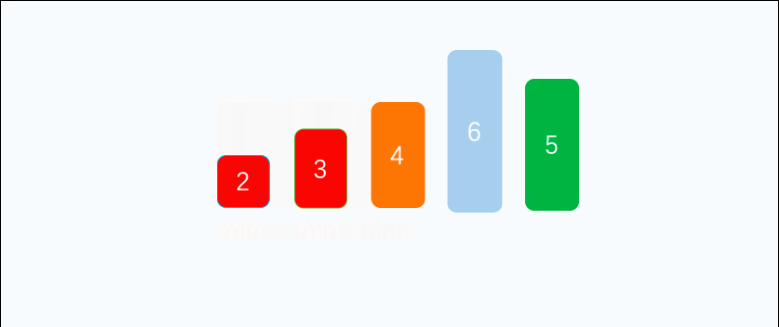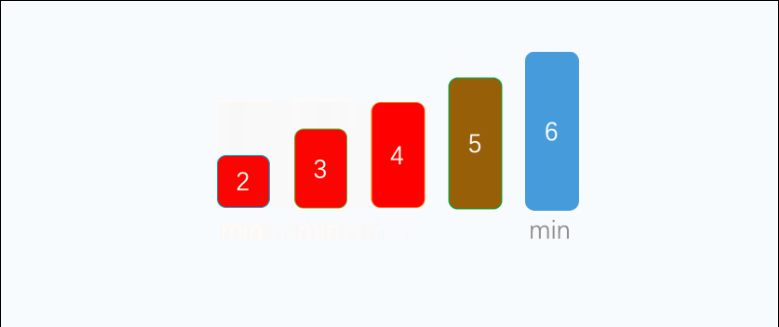
完整代码:
package com.keafmd.Sequence;
/**
* Keafmd
*
* @ClassName: SelectSort
* @Description: 选择排序
* @author: 牛哄哄的柯南
* @date: 2021-06-24 10:33
*/
public class SelectSort {
//直接选择排序
public static void selectSort(int[] arr, boolean ascending) {
for (int i = 0; i < arr.length; i++) {
int m = i; //最小值或最小值的下标
for (int j = i + 1; j < arr.length; j++) {
if (ascending ? arr[j] < arr[m] : arr[j] > arr[m]) {
m = j; //找到待排序的数中最小或最大的那个数,记录下标
}
}
//交换位置
int temp = arr[i];
arr[i] = arr[m];
arr[m] = temp;
}
}
public static void selectSort(int[] arr) {
selectSort(arr, true);
}
}
堆排序
先理解下大顶堆和小顶堆,看图
大顶堆,双亲结点的值比每一个孩子结点的值都要大。根结点值最大
小顶堆,双亲结点的值比每一个孩子结点的值都要小。根结点值最小

简单解释: 构建好大顶堆或小顶堆结构,这样最上面的就是最大值或最小值,那么我们取出堆顶元素,然后重新构建结构,一直取,一直重新构建,那么最后达到排序的效果了。

完整代码:
package com.keafmd.Sequence;
/**
* Keafmd
*
* @ClassName: HeapSort
* @Description: 堆排序
* @author: 牛哄哄的柯南
* @date: 2021-06-24 10:34
*/
public class HeapSort {
//堆排序
public static void heapSort(int[] arr) {
//对传入的数组进行建立堆,这里默认建立大顶堆,进行升序排列
heapSort(arr, true);
}
public static void heapSort(int[] arr, boolean maxheap) {
//1.构建大顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
//从第一个非叶子结点从下至上,从右至左调整结构
sift(arr, i, arr.length , maxheap);
}
//2.调整堆结构+交换堆顶元素与末尾元素
for (int j = arr.length - 1; j > 0; j--) {
//现在的数组第一个就是根结点,最小值所在,进行交换,把它放到最右边
int temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
//重新建立堆
sift(arr, 0, j , maxheap); //重新对堆进行调整
}
}
//建立堆的方法
/**
* 私有方法,只允许被堆排序调用
*
* @param arr 要排序数组
* @param parent 当前的双亲节点
* @param len 数组长度
* @param maxheap 是否建立大顶堆
*/
private static void sift(int[] arr, int parent, int len, boolean maxheap) {
int value = arr[parent]; //先取出当前元素i
for (int child = 2 * parent + 1; child < len; child = child * 2 + 1) { //从parent结点的左子结点开始,也就是2*parent+1处开始
if (child+1 < len && (maxheap ? arr[child] < arr[child + 1] : arr[child] > arr[child + 1])) { //如果左子结点小于右子结点,child指向右子结点
child++; //右孩子如果比左孩子大,我们就将现在的孩子换到右孩子
}
//判断是否符合大顶堆的特性, 如果右孩子大于双亲,自然左孩子也大于双亲,符合
//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
if (maxheap ? value < arr[child] : value > arr[child]) {
arr[parent]=arr[child];
parent = child;
}
else {//如果不是,说明已经符合我们的要求了。
break;
}
}
arr[parent] =value; //将value值放到最终的位置
}
}
总结
本篇文章就到这里了,希望能给你带来帮助,也希望您能够多多关注自由互联的更多内容!
