二叉树的四种遍历方式:
- 二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有的结点,使得每个结点被访问依次且仅被访问一次。
四种遍历方式分别为:先序遍历、中序遍历、后序遍历、层序遍历。

遍历之前,我们首先介绍一下,如何创建一个二叉树,在这里用的是先建左树在建右树的方法,
首先要声明结点TreeNode类,代码如下:
public class TreeNode {
public int data;
public TreeNode leftChild;
public TreeNode rightChild;
public TreeNode(int data){
this.data = data;
}
}
再来创建一颗二叉树:
/**
* 构建二叉树
* @param list 输入序列
* @return
*/
public static TreeNode createBinaryTree(LinkedList<Integer> list){
TreeNode node = null;
if(list == null || list.isEmpty()){
return null;
}
Integer data = list.removeFirst();
if(data!=null){
node = new TreeNode(data);
node.leftChild = createBinaryTree(list);
node.rightChild = createBinaryTree(list);
}
return node;
}
接下来按照上面列的顺序一一讲解,
首先来看前序遍历,所谓的前序遍历就是先访问根节点,再访问左节点,最后访问右节点,
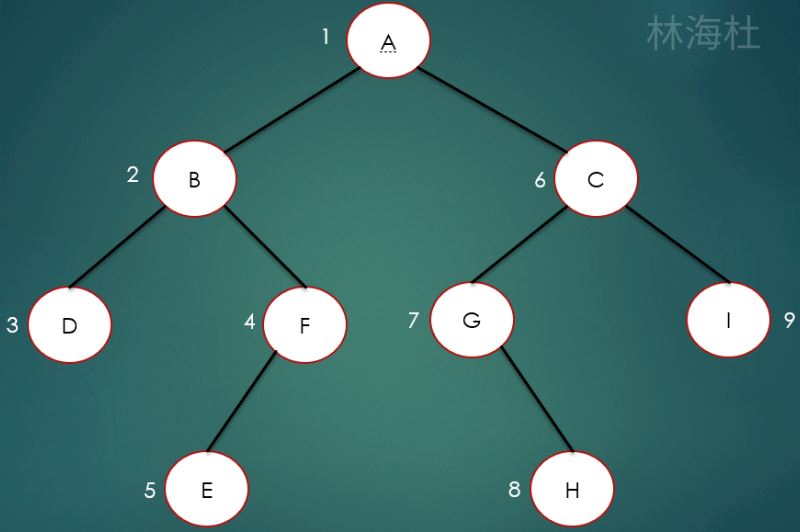
如上图所示,前序遍历结果为:
ABDFECGHI
实现代码如下:
/**
* 二叉树前序遍历 根-> 左-> 右
* @param node 二叉树节点
*/
public static void preOrderTraveral(TreeNode node){
if(node == null){
return;
}
System.out.print(node.data+" ");
preOrderTraveral(node.leftChild);
preOrderTraveral(node.rightChild);
}
再者就是中序遍历,所谓的中序遍历就是先访问左节点,再访问根节点,最后访问右节点,
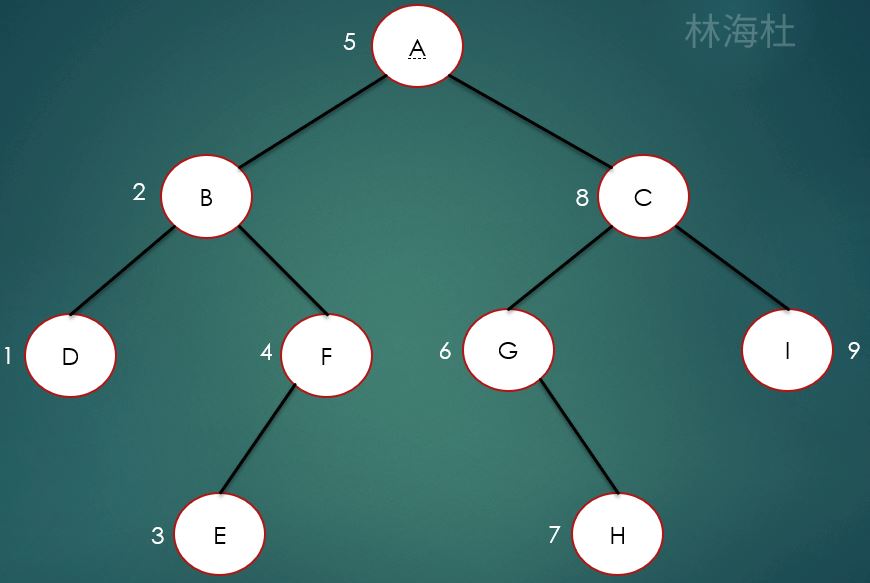
如上图所示,中序遍历结果为:
DBEFAGHCI
实现代码如下:
/**
* 二叉树中序遍历 左-> 根-> 右
* @param node 二叉树节点
*/
public static void inOrderTraveral(TreeNode node){
if(node == null){
return;
}
inOrderTraveral(node.leftChild);
System.out.print(node.data+" ");
inOrderTraveral(node.rightChild);
}
最后就是后序遍历,所谓的后序遍历就是先访问左节点,再访问右节点,最后访问根节点。
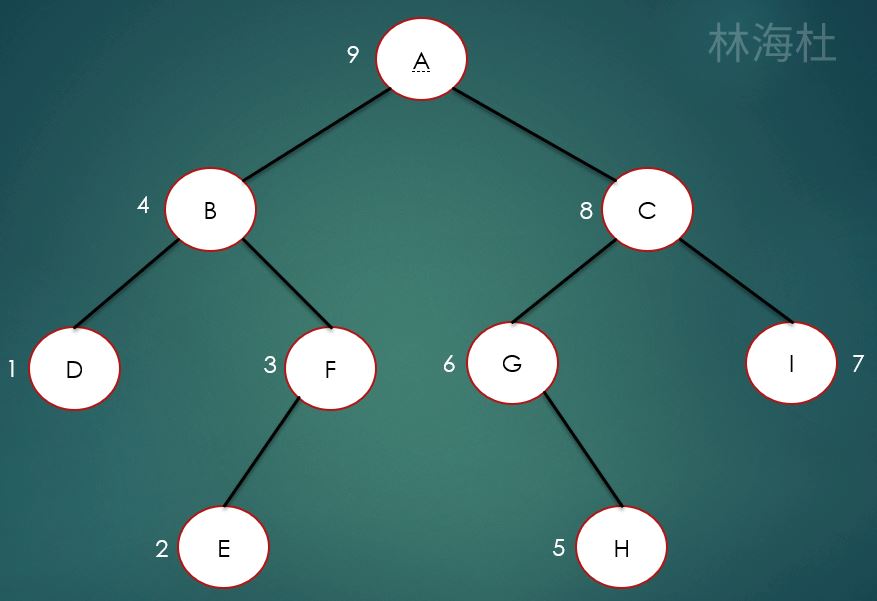
如上图所示,后序遍历结果为:
DEFBHGICA
实现代码如下:
/**
* 二叉树后序遍历 左-> 右-> 根
* @param node 二叉树节点
*/
public static void postOrderTraveral(TreeNode node){
if(node == null){
return;
}
postOrderTraveral(node.leftChild);
postOrderTraveral(node.rightChild);
System.out.print(node.data+" ");
}
讲完上面三种递归的方法,下面再给大家讲讲非递归是如何实现前中后序遍历的
还是一样,先看非递归前序遍历
1.首先申请一个新的栈,记为stack;
2.声明一个结点treeNode,让其指向node结点;
3.如果treeNode的不为空,将treeNode的值打印,并将treeNode入栈,然后让treeNode指向treeNode的右结点,
4.重复步骤3,直到treenode为空;
5.然后出栈,让treeNode指向treeNode的右孩子
6.重复步骤3,直到stack为空.
实现代码如下:
public static void preOrderTraveralWithStack(TreeNode node){
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode treeNode = node;
while(treeNode!=null || !stack.isEmpty()){
//迭代访问节点的左孩子,并入栈
while(treeNode != null){
System.out.print(treeNode.data+" ");
stack.push(treeNode);
treeNode = treeNode.leftChild;
}
//如果节点没有左孩子,则弹出栈顶节点,访问节点右孩子
if(!stack.isEmpty()){
treeNode = stack.pop();
treeNode = treeNode.rightChild;
}
}
}
中序遍历非递归,在此不过多叙述具体步骤了,
具体过程:
1.申请一个新栈,记为stack,申请一个变量cur,初始时令treeNode为头节点;
2.先把treeNode节点压入栈中,对以treeNode节点为头的整棵子树来说,依次把整棵树的左子树压入栈中,即不断令treeNode=treeNode.leftChild,然后重复步骤2;
3.不断重复步骤2,直到发现cur为空,此时从stack中弹出一个节点记为treeNode,打印node的值,并让treeNode= treeNode.right,然后继续重复步骤2;
4.当stack为空并且cur为空时结束。
public static void inOrderTraveralWithStack(TreeNode node){
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode treeNode = node;
while(treeNode!=null || !stack.isEmpty()){
while(treeNode != null){
stack.push(treeNode);
treeNode = treeNode.leftChild;
}
if(!stack.isEmpty()){
treeNode = stack.pop();
System.out.print(treeNode.data+" ");
treeNode = treeNode.rightChild;
}
}
}
后序遍历非递归实现,后序遍历这里较前两者实现复杂一点,我们需要一个标记位来记忆我们此时节点上一个节点,具体看代码注释
public static void postOrderTraveralWithStack(TreeNode node){
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode treeNode = node;
TreeNode lastVisit = null; //标记每次遍历最后一次访问的节点
while(treeNode!=null || !stack.isEmpty()){//节点不为空,结点入栈,并且指向下一个左孩子
while(treeNode!=null){
stack.push(treeNode);
treeNode = treeNode.leftChild;
}
//栈不为空
if(!stack.isEmpty()){
//出栈
treeNode = stack.pop();
/**
* 这块就是判断treeNode是否有右孩子,
* 如果没有输出treeNode.data,让lastVisit指向treeNode,并让treeNode为空
* 如果有右孩子,将当前节点继续入栈,treeNode指向它的右孩子,继续重复循环
*/
if(treeNode.rightChild == null || treeNode.rightChild == lastVisit) {
System.out.print(treeNode.data + " ");
lastVisit = treeNode;
treeNode = null;
}else{
stack.push(treeNode);
treeNode = treeNode.rightChild;
}
}
}
}
最后再给大家介绍一下层序遍历
具体步骤如下:
1.首先申请一个新的队列,记为queue;
2.将头结点head压入queue中;
3.每次从queue中出队,记为node,然后打印node值,如果node左孩子不为空,则将左孩子入队;如果node的右孩子不为空,则将右孩子入队;
4.重复步骤3,直到queue为空。
实现代码如下:
public static void levelOrder(TreeNode root){
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
root = queue.pop();
System.out.print(root.data+" ");
if(root.leftChild!=null) queue.add(root.leftChild);
if(root.rightChild!=null) queue.add(root.rightChild);
}
}
总结
本篇文章就到这里了,希望能够给你带来帮助,也希望您能够多多关注自由互联的更多内容!
