java中1+1d/5和1+1/5的区别说明

目录

• java 1+1d/5和1+1/5的区别
• 主要区别就是数据类型不同
• 计算1+1/2!+1/3!+...+1/20!之和

java 1+1d/5和1+1/5的区别

主要区别就是数据类型不同

1+1d/5的结果是1.2, 是double类型. 因为1d就是double类型,1d/5结果自动提升成double类型,1+1d/5结果也自动提升成double类型. .

1+1/5的结果1, 是int类型, 因为1/5是整除(会丢失小数部分的精度…) . 两边操作数都是int类型. 最后在加上1还是int类型.所以结果就是int类型.

java参考代码如下

public class Test {
public static void main(String[] args) {
    double num1 = 1 + 1d / 5;
    System.out.println(num1);//输出1.2
    int num2    = 1 + 1 / 5;
    System.out.println(num2);//输出1
 }
}

计算1+1/2!+1/3!+...+1/20!之和

原题：计算1+1/2!+1/3!+…+1/20!之和

观察题目，本题难点就是要计算阶乘，不妨用一个循环来计算阶乘，再用一个循环来计算从1/1！到1/20！的和。代码如下

package java1;
public class sum {
   public static void main(String args[]) {
	   //用s来表示阶乘结果
	   int s=1;
	   double sum=0;
	  //计算1/1！到1/20！的和
	   for(int i=1;i<=20;i++) {
		   //分别计算j从1到20的阶乘
		   for(int j=1;j<=i;j++) {
			   s=s*j;
		   }
		   sum+=1.0/s;
	   }
	   System.out.println(sum);
   }
}

这个输出结果为无穷，我当时想半天也没结果，后来同学指出我每次算每个数的阶乘时并没有将重置为1；所以正确代码如下

package java1;
public class sum {
   public static void main(String args[]) {
	   //用s来表示阶乘结果
	   double sum=0;
	  //计算1/1！到1/20！的和
	   for(int i=1;i<=20;i++) {
		   //每次算完阶乘后，计算下一次阶乘时都要将s重置为1
		   int s=1;
		   //分别计算j从1到20的阶乘
		   for(int j=1;j<=i;j++) {
			   s=s*j;
		   }
		   sum+=1.0/s;
	   }
	   System.out.println(sum);
   }
}

正确结果如下

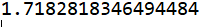
可以观察到上面代码的时间复杂度为o(n^2),我们其实可以思考一下如何运用优化阶乘，我这里听老师说阶乘可以运用递归思想。代码如下

package java1;
public class sum {
	//运用递归用来计算从1到20分别的阶乘结果
	public static int JieChen(int i) {
		   if(i==1) {
			   return 1;
		   }
		   else {
			   return (JieChen(i-1)*i);
		   }
	}
   public static void main(String args[]) {
	   double sum=0;
	  //计算1/1！到1/20！的和
	   for(int i=1;i<=20;i++) {
		   int s;
		   //用来计算i的阶乘
		   s=JieChen(i);
		   sum+=1.0/s;
	   }
	   System.out.println(sum);
   }
}

运用上面思路不仅可以计算有限的阶乘分之一的和，而且我们还可以拓展到计算无限个

以上为个人经验，希望能给大家一个参考，也希望大家多多支持自由互联。