目录 1.问题描述 2.确定程序框架 3.判断车牌k是是否为某个数的平方,是就输出 4.完整程序 5.运行结果 6.优化算法 1.问题描述 一辆卡车违反交通规则,撞人后逃跑。现场有三人目击该事件
目录
- 1.问题描述
- 2.确定程序框架
- 3.判断车牌k是是否为某个数的平方,是就输出
- 4.完整程序
- 5.运行结果
- 6.优化算法
1.问题描述
一辆卡车违反交通规则,撞人后逃跑。现场有三人目击该事件,但都没有记住车号,只记下了车号的一些特征。甲说:牌照的前两位数字是相同的:乙说:牌照的后两位数字是相同的,但与前两位不同:丙是数学家,他说:4位的车号刚好是一个整数的平方。请根据以上线索求出车号。
2.确定程序框架
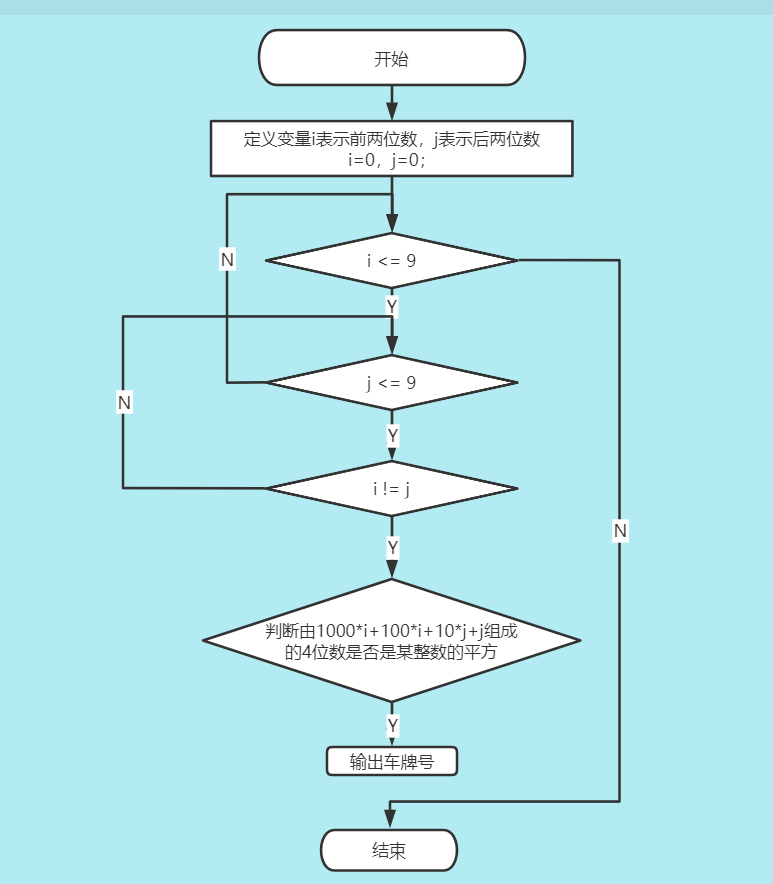
根据流程,构建程序框架如下:
if __name__ == '__main__':
# i代表前两位车牌号数字,j代表后两位车牌号数字,k代表车牌号
for i in range(10):
for j in range(10): # 穷举前两位和后两位车牌数字
# 判断前两位和后两位数字是否相同
if i != j:
# 组成4位车牌号码
k = 1000 * i + 100 * i + 10 * j + j
# 判断k是否是某个数的平方,是就输出
3.判断车牌k是是否为某个数的平方,是就输出
再次利用循环来实现,循环变量 temp求平方后和车牌号k比较,相等则投到车牌号,优化算法,temp的初值应该从31开始,因为小于30的数的平方小于4位数。故该层循环为最内层循环,对每一个年牌号均作如此操作。
for temp in range(31, 100):
if temp * temp == k:
print("车牌号为:", k)
4.完整程序
根据上面的分析,完整程序如下:
if __name__ == '__main__':
# i代表前两位车牌号数字,j代表后两位车牌号数字,k代表车牌号
for i in range(10):
for j in range(10): # 穷举前两位和后两位车牌数字
# 判断前两位和后两位数字是否相同
if i != j:
# 组成4位车牌号码
k = 1000 * i + 100 * i + 10 * j + j
# 判断k是否是某个数的平方,是就输出
for temp in range(31, 100):
if temp * temp == k:
print("车牌号为:", k)
5.运行结果
在Pycharm运行程序,结果如下
车牌号为: 7744
6.优化算法
针对上述程序,如果已经找到相应的车牌号,请读者考虑循环是否还需要继续呢?答案是肯定的,因为算法在设计穷举循环的时候,并没有在找到车牌的时候就退出循环,而是继续穷举其他i、j的情况。我们可以改进算法,设置一个“标识变量”,该变量初值为0,一旦找到车牌号,则改变该标识变量的值为1,每次循环判断一下标识变量的值。如果值为1,则退出所有循环,这样能有效的减少循环次数,
改进的程序如下:
if __name__=="__main__":
# i代表前两位车牌号数字,j代表后两位车牌号的数字,k代表车牌号
flog = 0 # 循环标识变量,为1时推出所有循环
for i in range(10):
if flog:
break
for j in range(10): # 穷举前两位和后两位车牌数字
if flog:
break
# 判断前两位和后两位数字是否相同
if i != j:
# 组成4位车牌号码
k = 1000 * i + 100 * i + 10 * j + j
# 判断k是否是某个数的平方,是就输出
for temp in range(31, 100):
if temp * temp == k:
print("车牌号为: ", k)
flog = 1
break
到此这篇关于python算法之抓交通肇事犯练习的文章就介绍到这了,更多相关python算法 内容请搜索易盾网络以前的文章或继续浏览下面的相关文章希望大家以后多多支持易盾网络!
