假设我们需要调查我们学校的身高发布,并且假设这个身高分布满足正态分布,那么我们的目的就是找到满足最符合这个分布的参数\(\mu和\sigma^2\),对此我们抽样取得数据,并且抽样样本\(n=200\)
似然函数对于以上问题,由于我们对参数\(\mu和\sigma^2\)未知,也就是我们对概率函数未知,并且我们的目的是由已知数据推导我们的概率参数,暂且对每个数据建立概率模型
\[P(x_i) = \frac 1 {\sqrt{2\pi}\sigma}e^{-\frac {(x_i-\mu)^2} {2\sigma^2}} \\ L(\theta)=L\left(x_{1}, x_{2}, \cdots, x_{n} ; \theta\right)=\prod_{i=1}^{n} p\left(x_{i} \mid \theta\right), \quad \theta \in \Theta \]上述公式的\(\theta\)表示概率参数的\(\mu和\sigma,L(\theta)\)表示多个数据的联合概率函数,那么对于这个函数的处理就用到了我们极大似然的思想,即我们的目的是\(max \ L(\theta)\),由于连乘符号不便于计算,以此取对数得到对数似然函数
\[H(\theta)=\ln L(\theta)=\ln \prod_{i=1}^{n} p\left(x_{i} \mid \theta\right)=\sum_{i=1}^{n} \ln p\left(x_{i} \mid \theta\right) \]极大似然思想就像我们对于线性回归时希望我们构造出来的曲线对已有数据的拟合最佳,这样才能更好的预测未来数据,极大似然的思想也是如此,希望对已有数据的解释最佳,也就是我们的概率函数要"站的住脚",就需要似然函数越大越好,这有点像数据的反推
计算极大似然的一般步骤- 写出似然函数;
- 对似然函数取对数,并整理;
- 求导数,令导数为 0,得到似然方程;
- 解似然方程,得到的参数。
对于一个抛硬币的问题,我们可以取随机变量X,它满足伯努利分布,假设\(p\)是硬币朝上的概率,\(q=1-p\),\(f(x|p)\)表示概率函数
\[f(x \mid p)= \begin{cases}p^{x} q^{1-x}, & \mathrm{x}=0,1 \\ 0, & x \neq 0,1\end{cases} \]但是我们假设我们获得了三个神奇的硬币,这三个硬币我们并不知道它正面朝上的概率,于是我们只能通过试验获得样本反推它的概率,这里就要用到我们的极大似然的方法,我们对这个问题建立相应的概率模型
试验由于技术问题,我们只能进行一下试验,对于三个硬币\(a,b,c\),我们抛三次硬币,如果\(a\)=1,那么我们取\(b\)的值,反之我们取\(c\)的值,(这里的取值是0和1,正面表示1,反面表示0)
\[假设对于三个硬币a,b,c它们的正面朝上的概率为\pi,p,q \\ \begin{aligned} P(y \mid \theta) &=\sum_{z} P(y, z \mid \theta)=\sum_{z} P(z \mid \theta) P(y \mid z, \theta) \\ &=\pi p^{y}(1-p)^{1-y}+(1-\pi) q^{y}(1-q)^{1-y} \end{aligned} \]符号说明: \(P(y|\theta)\)表示再概率参数\(\pi,p,q\)下y的取值概率,\(z\)表示硬币\(a\)的取值,作为本次试验的隐数据(因为我们并不对\(a\)的取值做统计,所以是为观测数据)
极大似然似然函数:
\[P(Y \mid \theta)=\prod_{i=1}^{n}\left[\pi p^{y_{f}}(1-p)^{1-y_{J}}+(1-\pi) q^{y_{j}}(1-q)^{1-y_{j}}\right] \]极大似然估计:
\[\hat{\theta}=\arg \max _{\theta} \log P(Y \mid \theta) \]好的,我们省略了中间的许多步骤,但是最终的目的是明确的,就是找到最佳的\(\theta\)来最大化我们的联合似然函数,但是问题来了,这个似然函数似乎不好计算,
- 变量不止一个,包含概率参数\(\pi,p,q\)
- 联合概率密度,要通过对数化计算
如果用一般的方法,我们似乎要废掉很多头发,但是这就是我要引入的EM算法,也就是说EM算法可以用来计算这种极大似然非常复杂的情况
Algorithm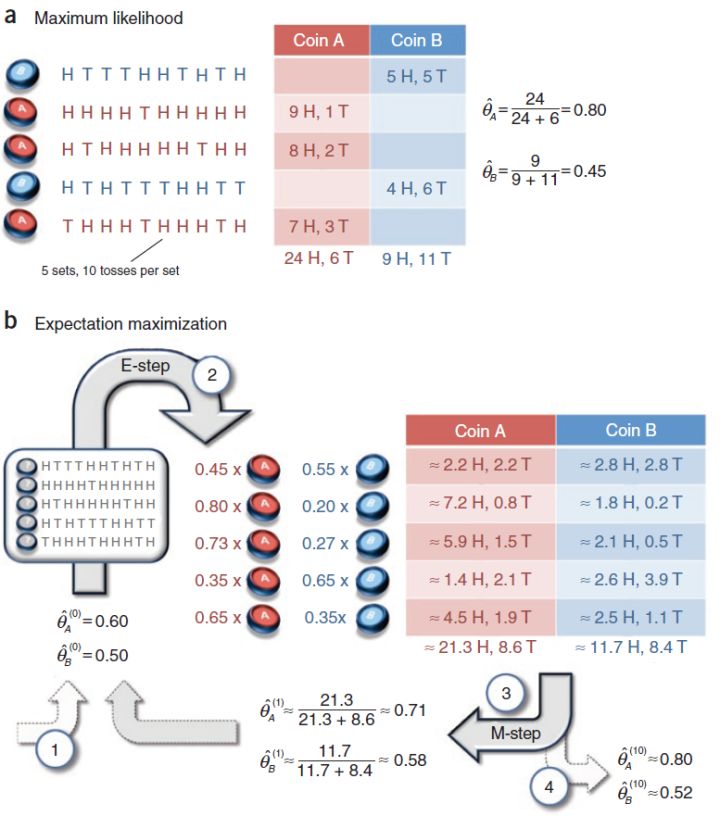
- 选取初值
- 获取样本
- 通过样本更新迭代参数值
- 多次迭代直到收敛
我们用三硬币问题来解释这个算法的步骤,
对于这个问题,我们首先把我们的概率参数\(\pi,p,q\)随机初始化获得初始值,再通过\(n\)次试验获得数据样本,对于样本的描述如下,我们已知进行了\(n\)次采样,并且获得了每次采样的值\(y_i\),接下来就是算法的第三步,通过样本结合概率函数来优化你的参数,这里的数学原理要仔细思考
对于每一次实验,我们可以得到我们的概率函数如下
\[X=1 \\ \alpha(y_i) = \frac {\pi p} {\pi p + (1-\pi)q} \\ \lambda(y_i) = \frac {(1-\pi) q} {\pi p + (1-\pi)q} \\ \]\[X=0\\ \beta(y_i) = \frac {\pi (1-p)} {\pi (1-p) + (1-\pi)(1-q)} \\ \gamma(y_i) = \frac {(1-\pi) (1-q)} {\pi(1-p)+(1-\pi)(1-q)} \]符号说明:
\(a(y_i)\)表示实验序号\(i\)下,实验结果\(X=1\),结果来自硬币\(b\)的概率;\(\lambda(y_i)\)表示同样条件下,结果来自硬币\(c\)的概率;\(\beta(y_i)\)表示实验结果\(X=0\),结果来源于硬币\(b\)的概率,\(\gamma(y_i)\)表示结果出自\(c\)的概率
那么我们可以给出下面的优化方程来迭代你概率参数
\[\pi = \frac {\sum_{x=1}\alpha(y_i)+\sum_{x=0}\beta(y_i)} {n} \\ p = \frac {\sum_{x=1}\alpha(y_i)} {\sum_{x=1}\alpha(y_i)+\sum_{x=0}\beta(y_i)} \\ q = \frac {\sum_{x=1}\lambda(y_i) } {\sum_{x=1}\lambda(y_i)+\sum_{x=0}\gamma(y_i)} \]理解上面的优化方程,那么EM算法的基本层面是没有问题了,这里就不能给出更过的解释了,其实也是一种基于先验计算后验的方法
后续就是循环迭代,对于这个算法其实和K-means算法有相似之处,并且可以说明的是,它和K-means都可以用于聚类模型
再循环迭代上,可以说明的是,对于循环的结束怎么判断,
- 参数变动小于临界值: $\left|\theta{(i+1)}-\theta{(i)}\right|<\varepsilon_{1} $
- Q函数变动小于临界值:\(\left\|Q\left(\theta^{(i+1)}, \theta^{(i)}\right)-Q\left(\theta^{(i)}, \theta^{(i)}\right)\right\|<\varepsilon_{2}\)
对于\(Q\)函数的解释: 完全数据的对数似然函数\(logP(Y,Z|Θ)\)关于在给定观测数 据Y和当前函数\(Θ(i)\)下对未观测数据Z的条件概率分布$ P(Z|Y, Θ(i))\(,的期望称为\)Q$函数
\[Q\left(\theta, \theta^{(l)}\right)=E_{Z}\left[\log P(Y, Z \mid \theta) \mid Y, \theta^{(l)}\right] \]对\(Q\)函数的理解具体看后面的数学推导
Mathematical Explanation of Algorithms我们已经了解了EM算法的步骤,但是对于其中较为深刻的数学原理还不知道,这里其中包括了一下几个问题,
- 为什么EM算法能近似实现对观测数据的极大似然估计
- 为什么在EM算法下,概率参数最终能够收敛
对于上面的一些问题包括Q函数的来源包含复杂的数学推导,由于这些的数学推导不简单,内容比较多,推荐取看李航的《统计学习方法》,这本书给出了详细的解释
Application of EM Algorithm 在高斯混合模型(GMM)上的运用EM算法的一个重要应用是高斯混合模型的参数估计,高斯混合模型应用广泛(比如机器学习的聚类),且由于他再极大似然上存在难度,所以EM算法是高斯混合模型参数估计的很有效的方法,
对于这个的具体内容可以详细看我的其他博客
在无监督学习上的应用 略
Conclusion自我收获: EM算法是我目前学习的数学推导最多的算法,算上去,我从了解各种概率模型开始,然后先验分布和后验分布,其中看了很多他人的博客,在最开始理解算法的时候是看了B站的复旦老师的课程,后面对公式理解最多的地方是从李航的书上
