废话不多说,我们直接上两个最常见的小例子:
一、递归,伪递归,迭代实现n!
package com.njbdqn.test02;
/**
* 递归,伪递归,迭代实现n!
*/
public class RecursionTest {
public static void main(String[] args) {
System.out.println(recurse(5)); //递归显示
System.out.println(camouflageRecurse(5, 1)); //伪递归
System.out.println(iteration(5)); //迭代
}
/**
* n的阶乘,尾递归实现方式
*
* @param n
* @param result 计算保存的中间结果
* @return 最终结果
*/
public static int camouflageRecurse(int n, int result) {
if (n == 1) {
return result;
} else {
result = result * n;
return camouflageRecurse(n - 1, result);
}
}
/**
* 求 n 的阶乘递归调用方式
*
* @param n n个数的阶乘
* @return n个数阶乘的结果
*/
public static int recurse(int n) {
if (n == 1) {
return 1;
} else {
return n * recurse(n - 1);
}
}
/**
* 用迭代的方法实现n的阶乘
*
* @param n
* @return
*/
public static int iteration(int n) {
int result = 1;
for (int i = 2; i <= n; ++i) {
result *= i;
}
return result;
}
}
二、斐波那契数列的递归和迭代实现求和
package com.njbdqn.test02;
/**
* 斐波那契数列的递归和迭代实现求和
* 0 1 1 2 3 5 8 13 21 34 55 89
*/
public class FibonacciTest {
public static void main(String[] args) {
System.out.println(fibonacciRecurse(14));
System.out.println(fibonacciIteration(14));
System.out.println(camouflageFibonacci(14,1,0));
}
/**
* 递归调用实现斐波那契数列
*
* @param n
* @return
*/
public static int fibonacciRecurse(int n) {
if (n == 1) {
return 0;
} else if (n == 2) {
return 1;
} else {
return fibonacciRecurse(n - 1) + fibonacciRecurse(n - 2);
}
}
/**
* 迭代实现斐波那契数列
* 0 1 1 2 3 5 8 13 21 34 55 89
*
* @param n
* @return
*/
public static int fibonacciIteration(int n) {
int fab = 0; //最终结果 n的值
int pre = 1; //记录n-1值
int p = 0; //记录n-2的位置
if (n == 1) {
fab = 0;
} else if (n == 2) {
fab = 1;
}
for (int i = 2; i < n; ++i) {
fab = pre + p;
p = pre;
pre = fab;
}
return fab;
}
/**
* 斐波那契数列尾递归实现
* 0 1 1 2 3 5 8 13 21 34 55 89
*
* @param n
* @return
*/
public static int camouflageFibonacci(int n, int result1,int result2) {
if (n == 0) {
return result1;
} else {
return camouflageFibonacci(n - 1, result2,result1+result2) ;
}
}
}
上述两个小例子我们都采用了迭代、递归和尾递归的方法去实现。迭代不必说,就是用我们java基础的 for 循环去实现。而在递归和尾递归实际上都是java 基础 oop 的自己调用自己方法的实现。尾递归实际上是对递归的优化。
递归
递归的本质是,某个方法中调用了自身。本质还是调用一个方法,只是这个方法正好是自身而已。
如第二个例子斐波那契数列的递归return fibonacciRecurse(n - 1) + fibonacciRecurse(n - 2)部分执行示意图如下所示:
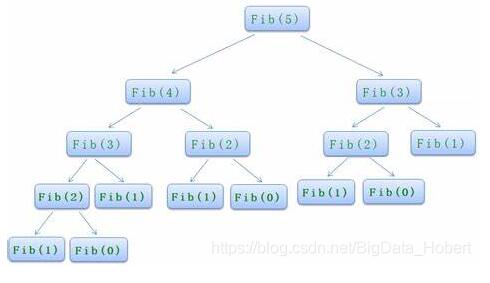
递归的三大特性:
调用的是同一个方法
因为调用的是同一个方法,所以只需要写一个方法,就可以让你轻松调用无数次,所以调用的方法数可能非常巨大,其实在实际问题中往往都是方法数调用巨大的情况。
在自身中调用自身,本身就是嵌套调用(栈帧无法回收,开销巨大)
递归的局限性:
因为递归调用的方法数大都非常巨大和嵌套调用带来的栈帧无法回收,所以递归调用最大的诟病就是开销巨大,栈帧和堆一起爆掉,俗称内存溢出泄露。
java为了优化递归带来的内存溢出泄露,就有了尾递归的诞生。那么尾递归是如何优化递归的呢?
尾递归
尾递归优化是利用上面的第一个特点 “调用同一个方法” 来进行优化的。为了解决递归的开销大问题,使用尾递归优化,具体分两种方法:
尾递归优化方式:
尾递归的形式:把递归调用的形式写成尾递归的形式
编译器对尾递归的优化:编译器碰到尾递归,自动按照某种特定的方式进行优化编译
尾递归的形式:
尾递归其实只是一种对递归的特殊写法,这种写法原本并不会带来跟递归不一样的影响,它只是写法不一样而已,写成这样不会有任何优化效果,该爆的栈和帧都还会爆
递归的本质是某个方法调用了自身,尾递归这种形式就要求:某个方法调用自身这件事,一定是该方法做的最后一件事(所以当有需要返回值的时候会是return f(n),没有返回的话就直接是f(n)了)
这个f(n)外不能加其他东西,因为这就不是最后一件事了,值返回来后还要再干点其他的活,变量空间还需要保留。比如如果有返回值的,你不能:乘个常数 return 3f(n);乘个n return n*f(n);甚至是 f(n)+f(n-1)…
另外,使用return的尾递归还跟函数式编程有一点关系
编译器对尾递归的优化
简单说就是重复利用同一个栈帧,不仅不用释放上一个,连下一个新的都不用开,效率非常高
一方面是因为在递归调用自身的时候,这一层函数已经没有要做的事情了,虽然被递归调用的函数是在当前的函数里,但是他们之间的关系已经在传参的时候了断了,也就是这一层函数的所有变量什么的都不会再被用到了,所以当前函数虽然没有执行完,不能弹出栈,但它确实已经可以出栈了
另一方面是正因为调用的是自身,所以需要的存储空间是一毛一样的,那干脆重新刷新这些空间给下一层利用就好了,不用销毁再另开空间
如第二个例子斐波那契数列的尾递归return camouflageFibonacci(n - 1, result2,result1+result2)部分执行示意图如下所示:

说到这里你很容易联想到JAVA中的自动垃圾回收机制,同是处理内存问题的机制,尾递归优化跟垃圾回收是不是有什么关系,这是不是就是JAVA不实现尾递归优化的原因?
垃圾回收(GC)与 尾递归
首先我们需要谈一下内存机制,这里我们需要了解内存机制的两个部分:栈和堆。
在Java中, JVM中的栈记录了线程的方法调用。每个线程拥有一个栈。在某个线程的运行过程中, 如果有新的方法调用,那么该线程对应的栈就会增加一个存储单元,即栈帧 (frame)。在frame 中,保存有该方法调用的参数、局部变量和返回地址。Java的参数和局部变量只能是 基本类型 的变量(比如 int),或者对象的引用(reference) 。因此,在栈中,只保存有基本类型的变量和对象引用。而引用所指向的对象保存在堆中。具体如下图所示:
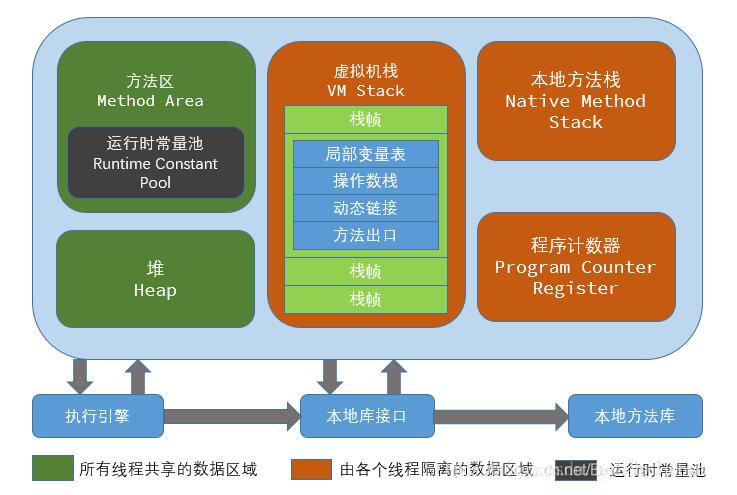
当被调用方法运行结束时,该方法对应的帧将被删除,参数和局部变量所占据的空间也随之释放。线程回到原方法,继续执行。当所有的栈都清空时,程序也随之运行结束。如上所述,栈 (stack)可以自己照顾自己。但堆必须要小心对待。堆是 JVM中一块可自由分配给对象的区域。当我们谈论垃圾回收 (garbage collection) 时,我们主要回收堆(heap)的空间。Java的普通对象存活在堆中。与栈不同,堆的空间不会随着方法调用结束而清空(即使它在栈上的引用已经被清空了)(也不知道为什么不直接同步清空)。因此,在某个方法中创建的对象,可以在方法调用结束之后,继续存在于堆中。这带来的一个问题是,如果我们不断的创建新的对象,内存空间将最终消耗殆尽。如果没有垃圾回收机制的话,你就需要手动地显式分配及释放内存,如果你忘了去释放内存,那么这块内存就无法重用了(不管是什么局部变量还是其他的什么)。这块内存被占有了却没被使用,这种场景被称之为内存泄露。
如下图所示:第二个例子斐波那契数列的尾递归每次调用自己的方法相当于在内存中缓存一个Object 的camouflageFibonacci 方法对象的引用,不会去释放,直到程序结束。
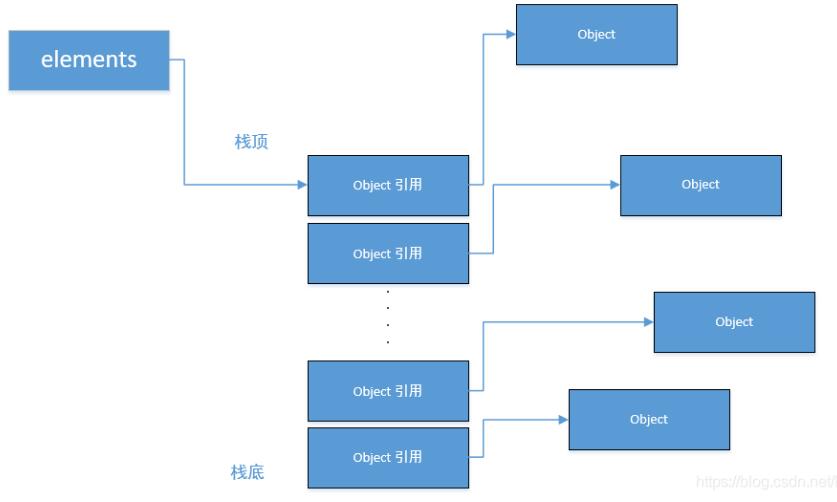
最原始的情况,都是需要手动释放堆中的对象,所以你经常需要考虑对象的生存周期,但是JAVA则引入了一个自动垃圾回收的机制,它能智能地释放那些被判定已经没有用的对象。
尾递归优化和垃圾回收最本质的区别是,尾递归优化解决的是内存溢出的问题,而垃圾回收解决的是内存泄露的问题。
内存泄露:指程序中动态分配内存给一些临时对象,但是对象不会被GC所回收,它始终占用内存。即被分配的对象可达但已无用。
内存溢出:指程序运行过程中无法申请到足够的内存而导致的一种错误。内存溢出通常发生于OLD段或Perm段垃圾回收后,仍然无内存空间容纳新的Java对象的情况。
从定义上可以看出内存泄露是内存溢出的一种诱因,不是唯一因素。
自动垃圾回收机制的特点是:
解决了所有情况下的内存泄露的问题,但还可以由于其他原因内存溢出
针对内存中的堆空间
正在运行的方法中的堆中的对象是不会被管理的,因为还有引用(栈帧没有被清空)
一般简单的自动垃圾回收机制是采用 引用计数 (reference counting)的机制。每个对象包含一个计数器。当有新的指向该对象的引用时,计数器加 1。当引用移除时,计数器减 1,当计数器为0时,认为该对象可以进行垃圾回收
与之相对,尾递归优化的特点是:
优化了递归调用时的内存溢出问题
针对内存中的堆空间和栈空间
只在递归调用的时候使用,而且只能对于写成尾递归形式的递归进行优化
正在运行的方法的堆和栈空间正是优化的目标
以上这篇两个小例子轻松搞懂 java 中递归与尾递归的优化操作就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持易盾网络。
