[笔记] 计算几何

其他的咕咕咕了，不喜欢计算几何 qaq

基本定义 向量

• \(\overrightarrow{PQ}=Q-P\)

叉积 二维 a.x * b.y-a.y * b.x 三维 sum += a.x * b.y * c.z + a.y * b.z * c.x + a.z * b.x * c.y sum -= a.z * b.y * c.x + a.y * b.x * c.z + a.x * b.z * c.y 基本操作 将一个向量旋转一定角度

Vec rotate(Vec a, LD b){
	LD s = sin(b), c = cos(b);
	return {a.x * c - a.y * s, a.x * s + a.y * c};
}

判断一个点在直线的哪边

有直线上的一点 \(P\)，直线的方向向量 \(v\)，想知道 \(Q\) 在直线哪边：

利用叉积的性质，若 \(\overrightarrow{PQ}\times v >0\)，则 \(Q\) 在直线逆时针方向，否则在顺时针方向。

bool Left(Vec a, Line b){ return cross(a - b.p , b.v) > 0; }

判断两圆之间的关系

返回的是公切线个数

int Pos(Circle a, Circle b){
	LD dis = Dis(a.O, b.O); if(a.r < b.r) swap(a, b);
	if(dis > a.r + b.r) return 4;
	if(dis == a.r + b.r) return 3;
	if(dis > a.r - b.r) return 2;
	if(dis == a.r - b.r) return 1;
	return 0;
}

求两条直线的交点

有直线 \(AB,CD\)，求交点 \(E\)：

首先确定是否只有一个交点，然后因为记录的是直线上的一个点和直线的方向向量，所以只需要知道这个点与交点的距离 \(l\) ，再将这个点沿方向向量平移 \(l\) 个单位长度即可。利用正弦定理求解

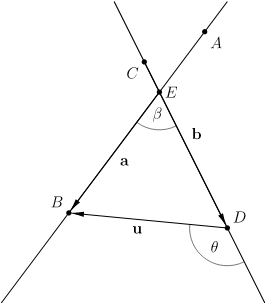
由上图可知，\(|\mathbf{a\times b|=|a||b|\sin\beta,|u\times b|=|u||b|\sin\theta}\)。

作商得：

\[T=\frac{\mathbf{|u\times b|}}{\mathbf{|a\times b|}}=\frac{|\mathbf{u}|\sin\theta}{|\mathbf{a}|\sin\beta}=l \]

交点即点 \(B+T\mathbf{a}\)。

Vec Inter(Line a, Line b){ return a.p + cross(b.v, (b.p - a.p)) / cross(b.v, a.v) * a.v;} 

求两圆的交点

注意要先判断有没有交点

pair <Vec, Vec> Inter(Circle a, Circle b){
	LD x = a.r, y = b.r, z = Dis(a.O, b.O);
	LD tar1 = acos((x * x + z * z - y * y) / (2 * x * z));
	Vec i1 = a.O + rotate(Line(a.O, b.O), tar1) / z * x;
	LD tar2 = acos((y * y + z * z - x * x) / (2 * y * z));
	Vec i2 = b.O + rotate(Line(b.O, a.O), tar2) / z * y;
	return {i1, i2};
}

求多边形周长

double PloygonDis(Vec *a, int n){
	double sum = 0;
	lfor(i, 1, n) sum += Dis(a[i], a[i % n + 1]);
	return sum;
}

求多边形面积

double PloygonArea(Vec *a, int n){
	double sum = 0;
	lfor(i, 3, n) sum += cross(a[i - 1] - a[1], a[i] - a[1]);
	return sum / 2;
}

极角排序 实现

1. 使用 atan2(y, x) 函数，返回值的范围是 \([-\pi,\pi]\)；
2. 使用叉积大于 \(0\) 的性质，注意因为叉积无法判 180 度以上，所以可能要结合象限排序；

凸包 二维凸包 特殊结论

• 二维平面四个点求凸包面积 \(\rightarrow\) 任选三个点面积之和 / 2

  二维平面三个点面积 \(\rightarrow\) 二个二维向量行列式值的绝对值 / 2

• 三维空间五个点求凸包体积 \(\rightarrow\) 任选四个点体积之和 / 2

  三维空间四个点体积 \(\rightarrow\) 三个三维向量行列式值的绝对值 / 6

半平面交 定义

有若干条有向直线，要求保留每条直线其中一侧，求最后保留的范围。

离线 \(O(n\log n)\)

用有向直线（一个点和一个方向向量）表示半平面，以下默认半平面在有向直线的左侧。
对有向直线按方向向量的极角排序，维护一个双端队列，存储当前构成半平面的直线以及相邻两直线的交点。
每次加入一条有向直线，如果队首 / 队尾的交点在直线右侧（用叉积判）则弹掉队首 / 队尾的直线。
需要注意的细节：

1. 加入直线时，先弹队尾，再弹队首。
2. 特判平行直线，在右侧的要弹掉。
3. 最后还要检查队尾交点是否在队首直线的右侧，如果是也要弹掉。
4. 如果题目给出的半平面不一定有限制边界，则应该手动加入一个 INF 边界。

double HPI(Line *a, int n){
	static deque <Vec> I; while(!I.empty()) I.pop_back(); 
	static deque <Line> Q; while(!Q.empty()) Q.pop_back();
	sort(a + 1, a + n + 1);
	Q.push_back(a[1]);
	lfor(i, 2, n){
		while(!I.empty() && Cross(a[i].v, I.back() - a[i].p) <= 0) I.pop_back(), Q.pop_back();
		while(!I.empty() && Cross(a[i].v, I.front() - a[i].p) <= 0) I.pop_front(), Q.pop_front();
		if(a[i].at2 != Q.back().at2) Q.push_back(a[i]);
		else if(Cross(a[i].v, Q.back().p - a[i].p) <= 0){
			Q.back() = a[i]; if(!I.empty()) I.pop_back();
		}else continue;
		auto qwq = Q.rbegin();
		if(Q.size() > 1) I.push_back(Inter(*(++qwq), Q.back()));
	}
	while(!I.empty() && Cross(Q.front().v, I.back() - Q.front().p) <= 0) I.pop_back(), Q.pop_back(); 
	if(Q.size() > 1) I.push_back(Inter(Q.front(), Q.back()));
	int cnt = 0; static Vec *b = new Vec[I.size() + 1];
	for(auto x : I) b[++cnt] = x;
	return PloygonDis(b, cnt);
}

积分 对积分的感性理解

\[\int_a^bf(x)\mathrm{d}x \]

• 有一个函数 \(f(x)\)，求其在区间 \([a,b]\) 与 \(x\) 轴围成的面积，\(x\) 轴上为正，\(x\) 轴下为负。

• 那么 \(\int\) 类比与 \(\sum\) 符号，同时用 \(\mathrm{d}x\) 表示将 \(x\) 分成很多很多很小的份。

• 同时也不难意识到，这个空间是封闭的才可以求面积。

如何积分

大部分的函数都是无法精确积分的，于是采用一些公式来逼近。

自适应辛普森积分

公式：

\[\int_a^b f(x) \mathrm{d}x = \frac{(b - a)(f(a) + f(b)+ 4f(\frac{a+b}{2}))}{6} \]

• 二次函数的积分可以精确计算，辛普森积分即是一种拿二次函数来拟合的方式。
• 在二次函数的情况下，该式求出的即准确积分，推导过程。

自适应：

因为 \(f(x)\) 不是二次函数，那么当然不能直接积分，于是就有了根据误差调整的自适应做法。

LD Ars(LD l, LD r, LD eps, LD val){
	LD mid = (l + r) / 2;
	LD L = simpson(l, mid), R = simpson(mid, r);
	if(fabs(L + R - val) <= eps) return L + R;
	return Ars(l, mid, eps / 2, L) + Ars(mid, r, eps / 2, R);
}

• 非常直接的想法，如果不满足 eps，就继续细分区间。
• 注意因为要合并两个区间，所以对误差的要求在提高。
• 因为是自适应的，所以复杂度玄学。
• 对于拟合易错的函数，可强制迭代一定层数。

积分在 OI 中的应用

一般用来求各种面积。

[CQOI2005]三角形面积并

没封装的简陋玩意

const LD Pi = acos(-1);

struct Vec{ LD x, y; };
void Out(Vec a){ cerr << a.x << ' ' << a.y << endl; }
void In(Vec &a){ scanf("%Lf%Lf", &a.x, &a.y); }
bool operator ==(Vec a, Vec b){ return a.x == b.x && a.y == b.y; }
bool operator !=(Vec a, Vec b){ return a.x != b.x || a.y != b.y; }
bool operator <(Vec a, Vec b){ return atan2(a.y, a.x) < atan2(b.y, b.x); }
LD atan2(Vec a){ return atan2(a.y, a.x); }
LD Cross(Vec a, Vec b){ return a.x * b.y - a.y * b.x; }
LD Dis(Vec a, Vec b){ return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); }
Vec operator -(Vec a, Vec b){ return {a.x - b.x, a.y - b.y}; }
Vec operator +(Vec a, Vec b){ return {a.x + b.x, a.y + b.y}; }
Vec operator /(Vec a, LD b){ return {a.x / b, a.y / b}; }
Vec operator *(Vec a, LD b){ return {a.x * b, a.y * b}; }
Vec operator *(LD b, Vec a){ return {a.x * b, a.y * b}; }
Vec rotate(Vec a, LD b){
	LD s = sin(b), c = cos(b);
	return {a.x * c - a.y * s, a.x * s + a.y * c};
}

struct Line{ 
	Vec p, v; LD at2; 
	Line(){}
	Line(Vec a, Vec b, LD c){ p = a, v = b, at2 = c; }
	Line(Vec a, Vec b){ p = a, v = b - a, at2 = atan2(v.y, v.x); } 
};
bool operator <(Line a, Line b){ return a.at2 < b.at2; }
bool Left(Vec a, Line b){ return Cross(a - b.p , b.v) > 0; }
Vec Inter(Line a, Line b){ return a.p + Cross(b.v, (b.p - a.p)) / Cross(b.v, a.v) * a.v;} 
Vec operator +(Vec a, Line b){ return {a.x + b.v.x, a.y + b.v.y}; }
Line rotate(Line a, LD b){ return {a.p, rotate(a.v, b), a.at2}; }
Line operator *(Line a, LD b){ return (Line){a.p, (Vec){a.v.x * b, a.v.y * b}, a.at2}; }
Line operator /(Line a, LD b){ return (Line){a.p, (Vec){a.v.x / b, a.v.y / b}, a.at2}; }

struct Circle{ Vec O; LD r; }; 
void In(Circle &a){ scanf("%Lf", &a.r), In(a.O); }
int Pos(Circle a, Circle b){
	LD dis = Dis(a.O, b.O); if(a.r < b.r) swap(a, b);
	if(dis > a.r + b.r) return 4;
	if(dis == a.r + b.r) return 3;
	if(dis > a.r - b.r) return 2;
	if(dis == a.r - b.r) return 1;
	return 0;
}
pair <Vec, Vec> Inter(Circle a, Circle b){
	LD x = a.r, y = b.r, z = Dis(a.O, b.O);
	LD tar1 = acos((x * x + z * z - y * y) / (2 * x * z));
	Vec i1 = a.O + rotate(Line(a.O, b.O), tar1) / z * x;
	LD tar2 = acos((y * y + z * z - x * x) / (2 * y * z));
	Vec i2 = b.O + rotate(Line(b.O, a.O), tar2) / z * y;
	return {i1, i2};
}

double PloygonArea(Vec *a, int n){
	double sum = 0;
	lfor(i, 3, n) sum += Cross(a[i - 1] - a[1], a[i] - a[1]);
	return sum / 2;
}
double PloygonDis(Vec *a, int n){
	double sum = 0;
	lfor(i, 1, n) sum += Dis(a[i], a[i % n + 1]);
	return sum;
}
double HPI(Line *a, int n){
	static deque <Vec> I; while(!I.empty()) I.pop_back(); 
	static deque <Line> Q; while(!Q.empty()) Q.pop_back();
	sort(a + 1, a + n + 1);
	Q.push_back(a[1]);
	lfor(i, 2, n){
		while(!I.empty() && Cross(a[i].v, I.back() - a[i].p) <= 0) I.pop_back(), Q.pop_back();
		while(!I.empty() && Cross(a[i].v, I.front() - a[i].p) <= 0) I.pop_front(), Q.pop_front();
		if(a[i].at2 != Q.back().at2) Q.push_back(a[i]);
		else if(Cross(a[i].v, Q.back().p - a[i].p) <= 0){
			Q.back() = a[i]; if(!I.empty()) I.pop_back();
		}else continue;
		auto qwq = Q.rbegin();
		if(Q.size() > 1) I.push_back(Inter(*(++qwq), Q.back()));
	}
	while(!I.empty() && Cross(Q.front().v, I.back() - Q.front().p) <= 0) I.pop_back(), Q.pop_back(); 
	if(Q.size() > 1) I.push_back(Inter(Q.front(), Q.back()));
	int cnt = 0; static Vec *b = new Vec[I.size() + 1];
	for(auto x : I) b[++cnt] = x;
	return PloygonDis(b, cnt);
}