题目链接:
题目描述
dls的算竞王国可以被表示为一个有 HH行和 WW列的网格,我们让 (i,j)(i,j)表示从北边第 ii行和从西边第 jj列的网格。最近此王国的公民希望国王能够修建一条铁路。
铁路的修建分为两个阶段:
1:从所有网格中挑选2个不同的网格,在这两个网格上分别修建一个火车站。在一个网络上修建一个火车站的代价是 Ai,j;
2:在这两个网格间修建一条铁轨,假设我们选择的网格是 (x1,y1)和(x2,y2),其代价是 C∗(|x1−x2|+|y1−y2|);
dls的愿望是希望用最少的花费去修建一条铁路造福公民们。现在请你求出这个最小花费。
题目输入
第一行输入三个整数分别代表H,W,C
接下来H行,每行W个整数,代表Ai,j
题目输出
输出一个整数代表最小花费
数据范围
2≤H,W≤1000
1≤C≤1e9
1≤Ai,j≤1e9
样例输入:
3 4 2
1 7 7 9
9 6 3 7
7 8 6 4
样例输出:
10
本题要求最小花费,即两个站点的费用+铁路费用(A(x1,y1)+A(x2,y2)+ C∗(|x1−x2|+|y1−y2|))。考虑去掉绝对值,转化成对两个点对应的费用的最小值问题。
(x1,y1) , (x2,y2)的位置关系有以下两种:
1. x2>=x1且y2>=y1 (x1!=x2&&y1!=y2)(主对角线上)费用: A(x1,y1)+A(x2,y2)+ C∗(|x1−x2|+|y1−y2|)
=A(x1,y1)+A(x2,y2) + C∗(x2 − x1) + C*(y2 − y1)
=A(x1,y1) - C ∗ (x1 + y1) + A(x2,y2) + C*(x2 + y2)
分成两部分,分别求最小值
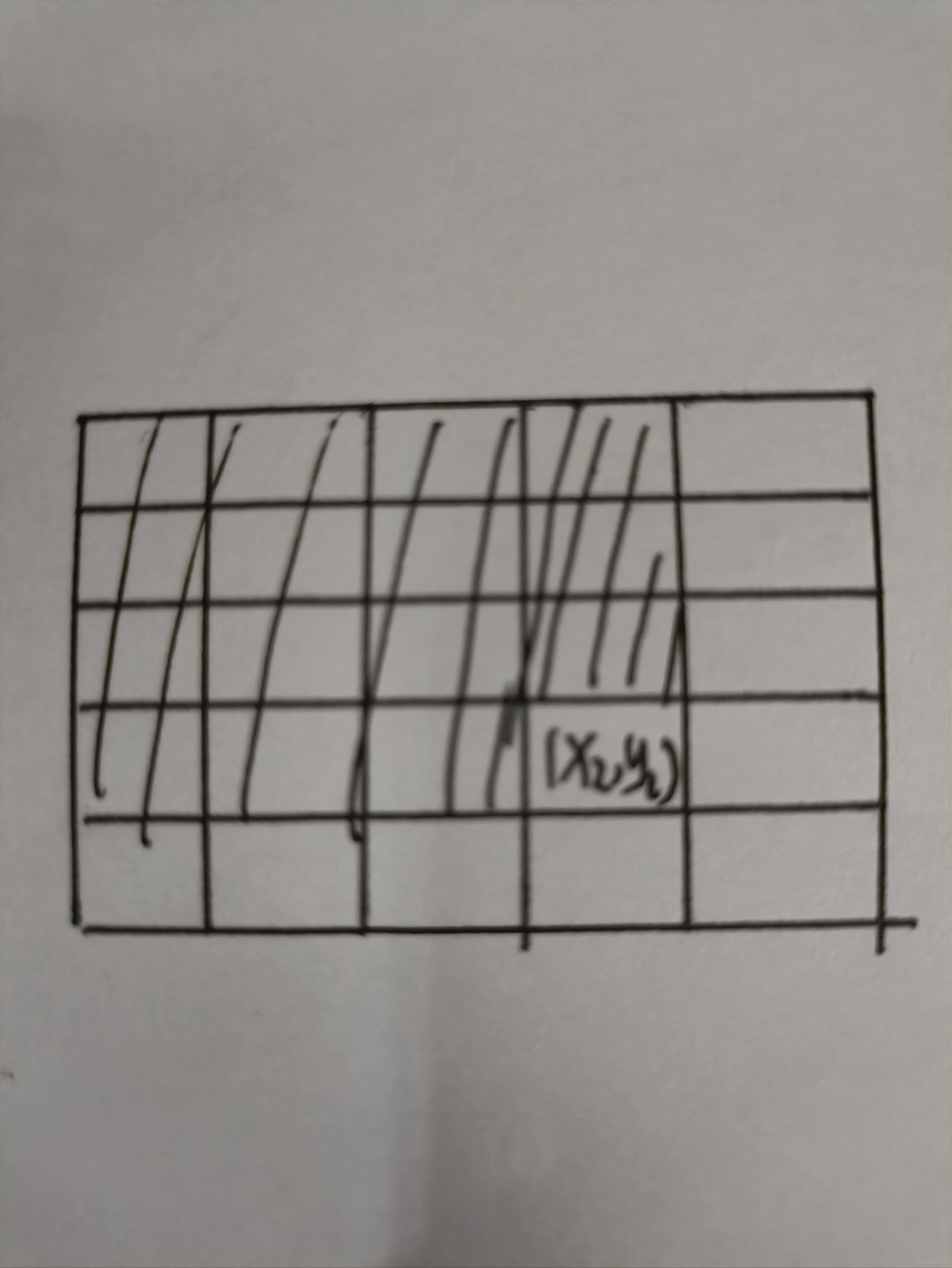
(图有点丑了,将就看看吧)
考虑枚举(x2,y2)的位置,满足x2>=x1且y2>=y1关系的点在图中阴影部分,快速求(x1,y1)的最佳位置,那么如何用O(1)的复杂度查询(x1,y1)的最佳位置呢?二维前缀最小值
2. x1>=x2且y2>=y1 (x1!=x2&&y1!=y2)(副对角线上)费用: A(x1,y1)+A(x2,y2)+ C∗(|x1−x2|+|y1−y2|)
=A(x1,y1)+A(x2,y2) + C∗(x1 − x2) + C*(y2 − y1)
=A(x1,y1) + C ∗ (x1 - y1) + A(x2,y2) + C*(y2 - x2)
分成两部分,分别求最小值
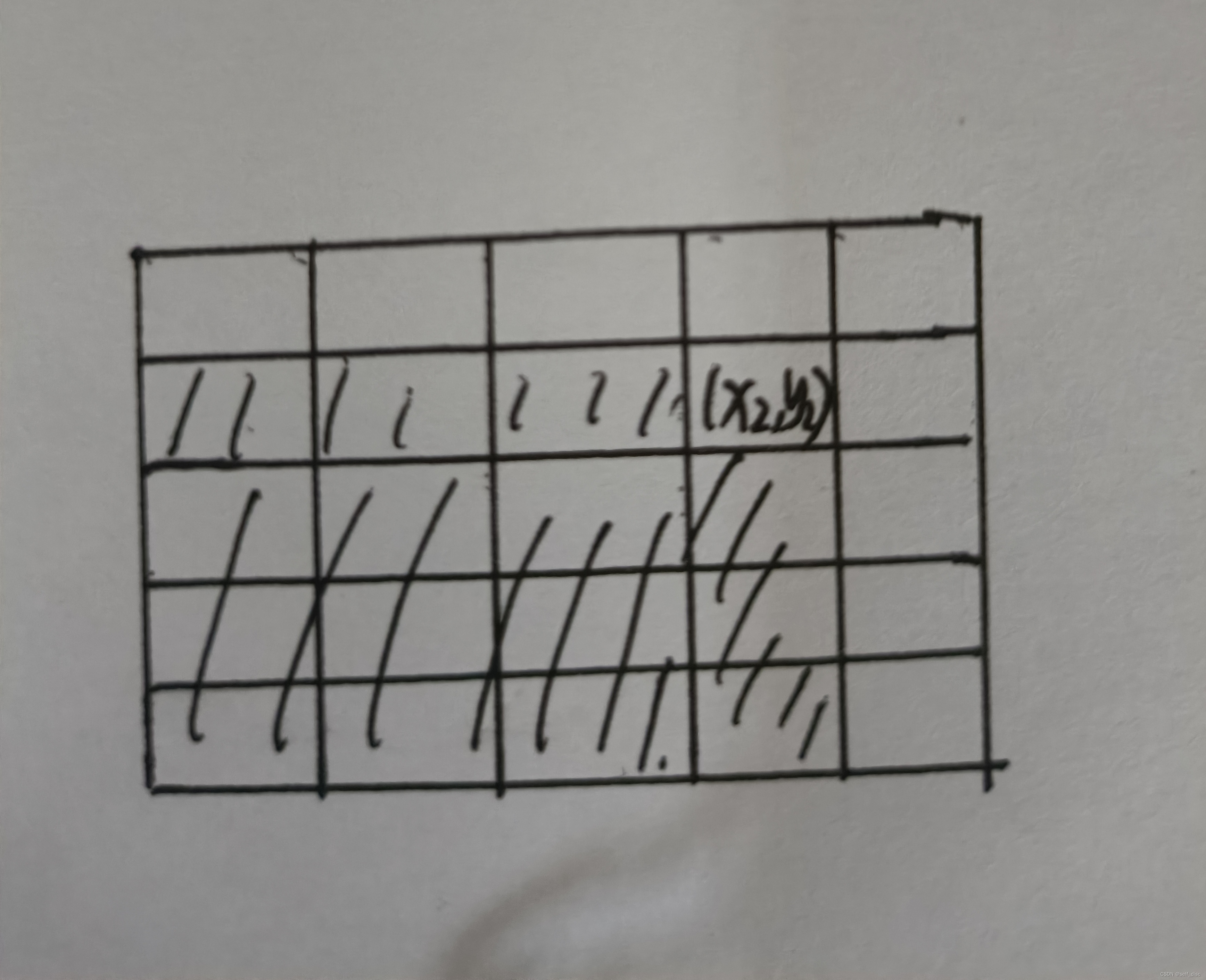
同上,考虑枚举(x2,y2)的位置,满足x1>=x2且y2>=y1关系的点在图中阴影部分,快速求(x1,y1)的最佳位置,O(1)的复杂度查询(x1,y1)的最佳位置呢?
二维前缀最小值二维前缀和:矩形每个元素值的和。
二位前缀最小值:矩形中每个元素值的最小值。
性质与二位前缀和类似,但又有所不同,二维前缀最小值不能求任意矩形区域的最小值,矩形的起点是固定的。此题刚好可以满足要求,利用二维前缀最小值的性质预处理在O(1)的复杂度下求出(x1,y1)的最佳位置。
那么如何预处理二维前缀最小值呢?
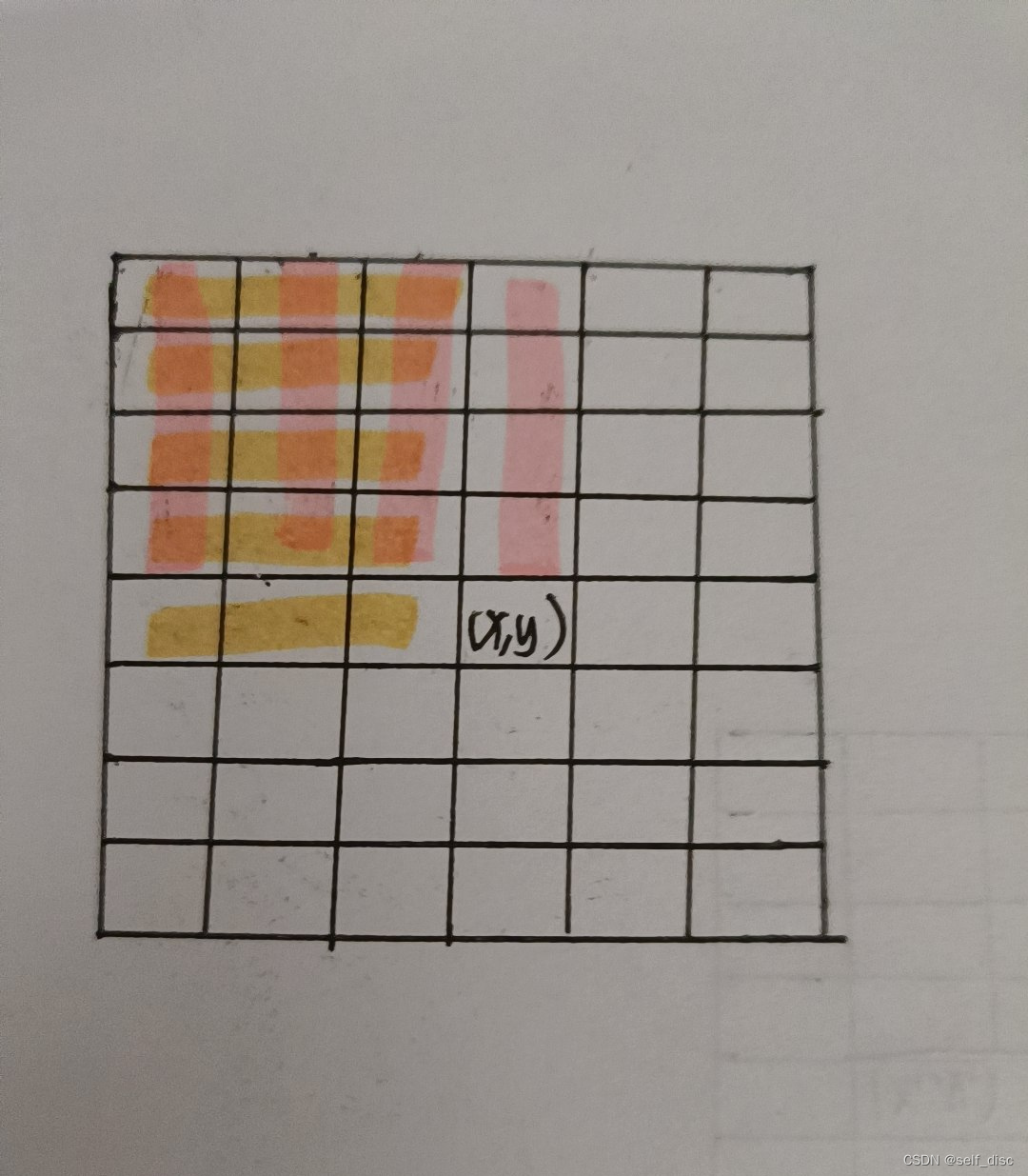
令f(i)(j)为以(1,1)为起点(i,j)为终点的矩形。
f(x,y)可以有图中红色区域和黄色区域转移而来,故而可得到转移方程
f (x , y) = min( f(x,y-1) ,f(x-1)(y),a(x)(y) )
详见代码
#include <bits/stdc++.h>
using namespace std;
#define int long long //一定要开longlong,没开longlong wa了三次,调半天的bug
int h, w, c, ans = 1e18;
int pre_min[1009][1009], pre_min2[1009][1009], a[1009][1009]; // pre_min为第一种情况下预处理的前缀最小值,pre_min2为第二种情况
signed main()
{
scanf("%lld%lld%lld", &h, &w, &c);
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
scanf("%lld", &a[i][j]); //输入
//情况一
for (int i = 0; i <= h; i++)
pre_min[i][0] = 1e18; //初始化!一定要开比较大,因为(i+j)*c最大可以达到2000*1e9!!!
for (int i = 0; i <= w; i++)
pre_min[0][i] = 1e18;
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
pre_min[i][j] = min(pre_min[i - 1][j], min(pre_min[i][j - 1], a[i][j] - c * (i + j))); //二维前缀最小值
for (int i = 1; i <= h; i++) //枚举(x2,y2)
for (int j = 1; j <= w; j++)
ans = min(ans, a[i][j] + c * (i + j) + min(pre_min[i - 1][j], pre_min[i][j - 1])); //更新最小值
//情况二
for (int i = 0; i <= h; i++) //初始化
pre_min2[i][0] = 1e18;
for (int i = 0; i <= w; i++)
pre_min2[h + 1][i] = 1e18; //这里有所不一样,二位前缀最小值的起点为(h,1)
for (int i = h; i >= 1; i--) //枚举(x2,y2)
for (int j = 1; j <= w; j++)
pre_min2[i][j] = min(pre_min2[i + 1][j], min(pre_min2[i][j - 1], a[i][j] + c * (i - j))); //二维前缀最小值
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
ans = min(ans, a[i][j] + c * (j - i) + min(pre_min2[i + 1][j], pre_min2[i][j - 1])); //更新最小值
cout << ans;
}