基础 哥德尔编码读paper-"云环境下集合隐私计算"的笔记
可以将非负整数序列(向量)与自然数建立起对应关系
具体来说,就是无穷序列\((a_1,x_2,...,x_m)\)借助素数序列\((p_1,p_2,...,p_m)\),建立对应关系:
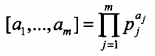
\([a_1,x_2,...,x_m]\)称作有穷序列\((a_1,x_2,...,x_m)\)的哥德尔数。
原理根据算数基本定理,任何自然数可以唯一分解为多个素数的乘积,而构成哥德尔数的素数序列\((p_1,p_2,...,p_m)\)是已知的,因此,由\([a_1,x_2,...,x_m]\)可以很容易得到序列\((a_1,x_2,...,x_m)\)。
同态加密算法该方案只用到了加法或者乘法同态性,下面分别介绍两种同态加密算法:
ElGamal具有乘法同态性,相比于RSA,能抵抗重放攻击(加密时加入了随机数)
1、加密结构:
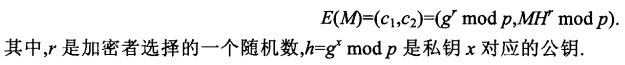
2、乘法计算:

具有加法同态性和一次"乘法"同态性,主要用到的还是加法同态
1、加密结构

2、加法计算


假设有\(n\)个集合\(X_1,...,X_n\),将每个集合\(X_i\)借助1-r编码方法编码成向量\(U_i\),然后将各个向量对应分量相乘后得到新的向量\(U'\):

如果向量\(U'\)中的某个分量\(u_j'\neq 1\),说明这n个向量的第\(j\)个分量不全为1,即n个集合中至少有一个集合含有元素\(u_j\),根据集合\(U;\)中不为1的分量,可以得到并集\(X_1\cup X_2\cup ...\cup X_n\),所以求集合的并集问题可以规约到计算向量\(U'\)
举例下面给出三个集合\(X_1,X_2,X_3\in U\),保密的计算集合的并集:
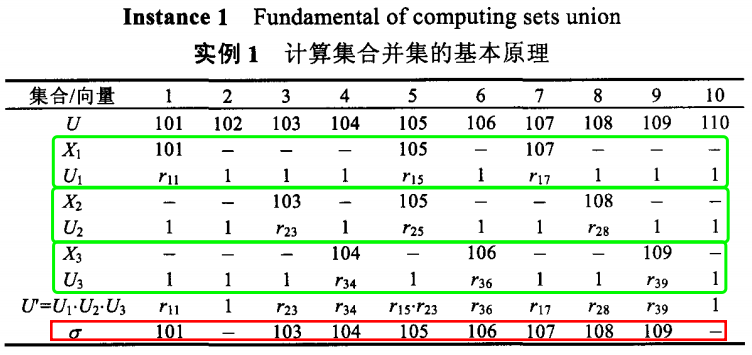
最后$\sigma $为集合的并集。
在云计算下,数据是需要加密来保证安全的,这里选用ElGamal加密算法。假设有\(n\)台服务器\(P_1,...,P_n\),每台服务器中有一个集合\(X_i\),假设第\(n\)台服务器\(P_n\)作为leader,生成加密的公私钥和参数,并将公钥和参数公开
(1)云服务器\(P_n\)将自己的公钥\(pk\)与参数\(params\)公开,并保留私钥\(sk\)

(2)每个云服务器\(P_i(i=1,...,n)\)计算:
-
将自己的秘密集合\(X_i\)编码为向量\(U_i\)
将\(X_i\)使用1-r编码方法编码为向量\(U_i=(u_{i,1},...,u_{i,m})\) -
将\(P_n\)的公钥\(pk\)与参数\(params\)加密\(U_i\)为\(E(U_i)\)
将向量\(U_i\)中的每个分量分别加密,即\(E(U_i)=(E(u_{i,1}),...,E(u_{i,m}))\) -
将密文向量\(E(U_i)\)随机分成\(k_i\)份并发送给\(n\)个云服务器中的\(k_i\)个
为了将数据混淆来保证\(U_i\)的安全,每台服务器需要将\(E(u_{i,j}),j=1,...,m\)分为\(k_i(k_i \leqslant n)\)份\(E(u_{i,j})_1,...,E(u_{i,j})_{k_i}\),(\(k_i\)其他服务器是不知道的),需要满足:\(E(u_{i,j})_1...E(u_{i,j})_{k_i}=E(u_{i,j})\)
\(P_i\)每次从每个密文分量\(E(u_{i,j})_1,...,E(u_{i,j})_{k_i}\)中选取一个,共选取\(k_i\)次,构成\(U_i\)的\(k_i\)份密文\(E(U_i)_1,...,E(U_i)_{k_i}\),每份(向量)里面\(m\)个元素。
如果直接对\(E(u_{i,j}),j=1,...,m\)进行分解因子,计算量大,所以这里使用模运算进行分解因子,具体如下:
选取\(k_i\)个随机数\(r_{i,1},..,r_{i,k_i}\in Z_p^*\),需要满足\(r_{i,1}....r_{i,k_i}=1 mod p\),从\(k_i\)个随机数中随机选择一个,如\(r_{i,1}\),和\(E(u_{i,j})\)相乘,即\(E(u_{i,j})_1=E(u_{i,j}).r_{i,1}\),然后将\(E(u_{i,j})_2,...,E(u_{i,j})_{k_i}\)用\(r_{i,2},...,r_{i,k_i}\)表示,进而就能将\(E(U_i)\)"拆分"为\(k_i\)份,且满足:\(E(u_{i,j})_1...E(u_{i,j})_{k_i}=r_{i,1}.E(u_{i,j}).r_{i,2}...r_{i,k_i}=E(u_i,j)\)
最后将这个\(k_i\)个密文向量\(E(U_i)_1,...,E(U_i)_{k_i}\)发送给k个云服务器(可以包括自己)。 -
把收到的所有密文向量对应的分量相乘得到新的密文向量\(E(U_i')\),并发送给\(P_n\)
每个云服务器\(P_i\)将密文发送后,也有可能收到其他云服务器发来的密文向量,\(P_i\)将收到的密文向量的每个相应分量分别相乘,构成新的密文向量\(E(U_i^*)=(E(u_{i,1}'),...,E(u_{i,m}^*))\),并发送给leader云服务器\(P_n\),从而将发送的密文和自身密文混淆。
(3)云服务器\(P_n\)计算: -
所有收到的密文向量对应的分量相乘,得到\(E(U')\)
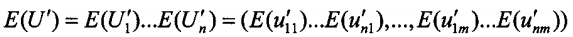
由于每个服务器都是半诚实的,不会加入额外的信息,所以\(P_n\)构造的密文向量\(E(U')\)是所有参与者密文向量各个分量的乘积,即:
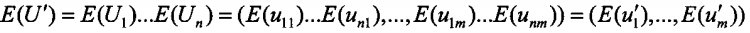
-
用自己的私钥\(sk\)解密\(E(U')\)得到\(U'\)
- 根据\(U'\)中不为1的分量得到\((\sigma _1,...,\sigma _h)\)
- 公布\((\sigma _1,...,\sigma _h)\)
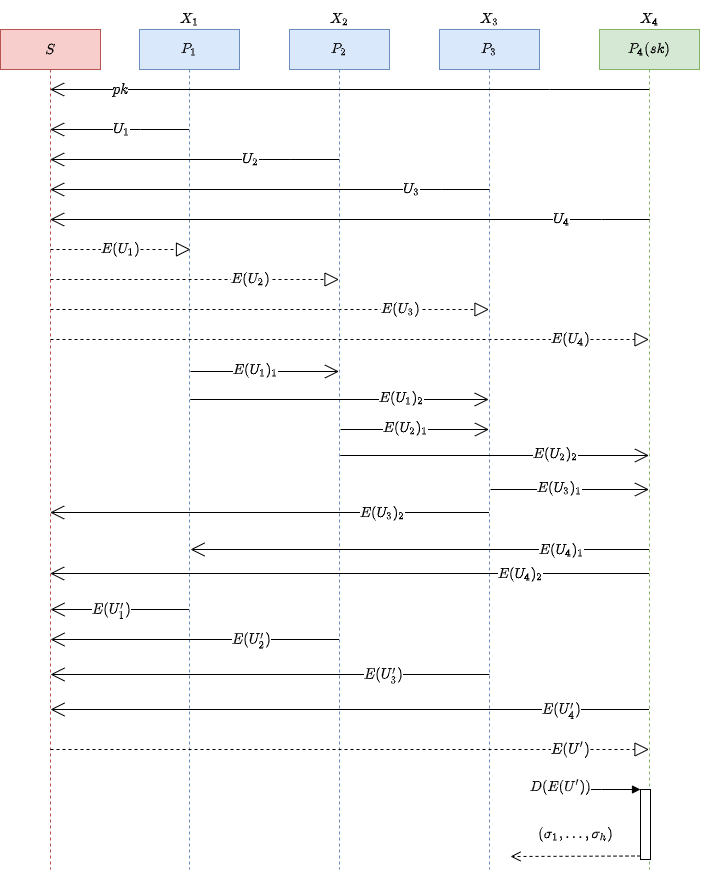
现在要求四个云服务器中的秘密数据的并集,假设\(P_4\)为leader服务器,\(k\)=3
(1)每台服务器\(P_i\)编码各自的集合数据\(X_i\)为\(U_i\);然后再使用公钥\(pk\)加密,即\(E(U_1),E(U_2),E(U_3),E(U_4)\);再将其拆分为\(k\)份,分别发送给其他两个服务器(自己留一份)
(2)在发送完后,\(P_i\)就有可能收到其他服务器发来的密文向量,然后将每份的密文向量对应的元素相乘得到\(E(U_i')\),发送给\(P_4\)
(3)\(P_4\)得到:
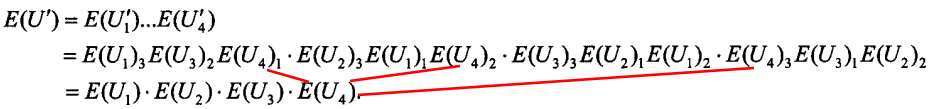
(4)\(P_4\)将\(E(U')\)解密,根据\(U'\)中不为1的元素得到并集\((\sigma _1 ,...,\sigma _h )\)

上面\(P_i\)将向量\(U_i\)加密,仅相当于加密1和随机数\(r \neq1\),E(1)和E(r)是公开的,只需要保密1和r所在的位置即可,因此可将加密运算外包给半可信的云服务器\(S\)。


以上改造,半可信云服务器得到的信息只有\(E(1),r,E(U_i')\),并不影响安全性。每个用户\(P_i\)仅需要计算少量的模乘,\(P_n\)只需要做\(m\)次解密,加密运算全部都由\(S\)完成,大大降低用户的计算量。
基本思想 0-r编码+哥德尔编码上面的方案计算复杂性和集合\(U\)中元素的个数\(m\)线性相关,若\(m\)较大,加密、解密的次数和通信量将会较大,不便于计算。若想要\(m\)不太大,可以在上面的基础上,利用哥德尔编码将向量对应成一个自然数的方法设计了一种高效的编码方法,使得协议的计算复杂性不再于集合的大小\(m\)相关,降低了计算复杂性。
(1)总集合\(U=(u_1,...,u_m),(u_1<....<u_m)\)对应集合\(P=(p_1,...,p_m),(p_1,...,p_m)\)是不等的互素数
(2)对于集合\(X_i\in U\),将其按照0-r编码方式编码为向量\(U_i=(u_{i,1},...,u_{i,m})\),具体是,若\(u_j\in X_i\),则\(u_{i,j}=r_{i,j}\),其中\(r_{i,j}\in [1,m]\)是一个随机数且\(r_{i,j}\neq 0\),否则\(u_{i,j}=0\),然后借助集合\(P\)利用哥德尔编码将\(U_i\)编码为一个自然数\(x_i\),即:
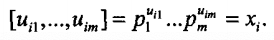
假设有\(n\)个集合\(X_1,...,X_n \in U\),将每个集合\(X_i\)按照上面的编码方式编码为一个自然数\(x_i\),将这\(n\)个自然数相乘得到\(x\),即:
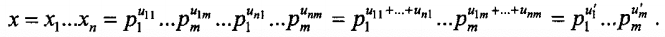
然后根据算数基本定理将\(x\)展开,得到集合\(U'={u_1',...,u_m'}\)。若\(u_j'=u_{1,j}+...+u_{n,j}\neq 0\),则说明\(n\)个集合中至少有一个集合中有\(u_j\)。所以就可以根据向量\(U'\)中不为0的分量,得到并集。
故计算并集的问题可以规约到计算\(x\)。

\(U\)集合是公开的,或者是\(P_n\)已知的;\(P_n\)作为leader。
输入:\(P_1,...,P_n\)各自的秘密集合\(X_1,..,X_n \in U\)
输出:交集\((\sigma _1,...,\sigma _h)\)
(1)云服务器\(P_n\)保留私钥\(sk\),公布公钥\(pk\)和系统参数\(params\)

(2)每个云服务器\(P_i\)计算如下:
-
根据上面改造的编码方法将自己的秘密集合\(X_i\)编码为自然数\(x_i\)
-
用公钥\(pk\)加密\(x_i\)为\(E(x_i)\)
直接发送\(E(x_i)\)是不安全的,因为\(P_n\)可以直接解密,所以需要混淆密文与云服务器的对应关系! -
将\(E(x_i)\)随机分为\(k_i\)份并发送给\(k_i\)个服务器

-
将收到的所有密文相乘得到新的密文\(E(x_i')\),并发送给\(P_n\)

(3)云服务器\(P_n\)计算如下:
- 把所有收到的密文相乘,得到\(E(x)\)
- 用私钥\(sk\)解密\(E(x)\)得到\(x\)
- 将\(x\)用算术基本定理展开得到向量\(U'\)
- 根据\(U'\)中不为0的分量得到集合\((\sigma _1,...,\sigma _h)\)


(1)用户自己编码,然后拆分混淆,发给服务器
(2)服务器计算(混淆后的明文),再加密,发送给leader服务器
(3)leader服务器计算(密文),解密,得到并集,并分发
方案分析云服务器没有任何一个云用户秘密向量的全部信息,因此得到不到云用户的信息
安全性证明
保密计算求集合交集方案协议上面介绍的是求集合的并集,现在求交集,变动不大!


(1)集合\(U=(101,102,103,104,105,106,107,108,109,110)\)对应集合\(P=(2,3,5,7,11,13,17,19,23,31)\),假设要计算3个集合\(X_1=(101,105,107),X_2=(103,105,108),X_3=(105,106,109)\)的交集,根据0-r编码将其编码为向量\(U_1,U_2,U_3\),即:
\[U_1=(0,1,2,3,0,4,0,5,6,7),U_2=(1,2,0,4,0,5,6,0,7,8),U_3=(1,2,3,4,0,0,7,8,0,9) \](2)将向量\(U_1,U_2,U_3\)借助集合\(P\)利用哥德尔编码编码为自然数\(x_1,x_2,x_3\),即:
\[x_1=[0,1,2,3,0,4,0,5,6,7]=3^1.5^2.7^3.13^4.19^5.23^6.31^7;x_2=[1,2,0,4,0,5,6,0,7,8]=2^1.3^2.7^4.13^5.17^6.23^7.31^8;x_3=[1,2,3,4,0,0,7,8,0,9]=2^1.3^2.5^3.7^4.17^7.19^8.31^9 \](3)将这三个自然数相乘得到:
\[x=x_1.x_2.x_3=2^2.3^5.5^5.7^{11}.11^0.13^9.17^{13}.19^{13}.21^{13}.31^{24} \](4)即得到向量\(U'=(2,5,5,11,0,9,13,13,13,24)\),根据向量\(U'\)中为0的分量得到交集:
\[X_1 \cap X_2 \cap X_3=(105) \]以上为了方便演示,省去了拆分的步骤。
