22-5-13 seminar上和大家分享了这篇文章,重新整理一下在博客里备个份
[0]Graph few-shot learning via knowledge transfer
起因是在MLNLP的公众号上看到了张初旭老师讲的小样本图学习,虽然没看到录像,但是把ppt下下来研究了一下。所以本文中出现的图片许多都是张老师ppt中的图,在张老师的主页上能够找到的这份PPT。
前置知识 图与图表示学习首先,老生常谈的,自然界中有许多的图数据和应用,包括社交的,安全的,医学的,化学的等等等等。
其中一种方法称为图表示学习,通过一个模型生成嵌入,可以用于下游任务中,包括节点级别的,边级别的,图级别的各种任务。 这里的嵌入指的是数据输入模型后得到的输出,往往是数据的低维表示。
这种图表示学习,对于具体的任务,非常依赖充足的标签数据。
于是就遇到了相应的挑战,在图上,有许多数据只有很少的标签数据。例如在社交图中有4000个以上的类别只有不到100个节点,在ins上的毒品交易,天生样本量就很少等等。
于是就发现小样本学习是研究这种问题的一个解决方案。
概念:小样本学习是一类具有很少监督信息,或者是几个标签的机器学习问题。
小样本学习的目标是,通过补充其他的训练数据来模拟目标的小样本学习任务,来从补充数据中学习到一种元知识。
具体来说,使用的是一种称为n-way k-shot 的学习方式。
如图所示,为一个5-way 1-shot的小样本学习。

way,指的是数据集中类别的数量,图中为5个类别。shot,指的是数据集中每个类别图片的数量,图中每个类别只有一张图片。
小样本学习分为两个阶段,第一个阶段称为元训练,第二个阶段称为元测试。然后每个数据集被分成两组,一组称为支持集,另一组叫查询集。这里需要明确的是,小样本学习会有非常非常多不同的数据集,每个数据集都十分的小,都被分成查询集和支持集两个部分。
在元训练的阶段,首先会用许多不同的数据集对模型进行训练,这些数据集的类别可以毫不相干。如上图所示,meta-training阶段的两个数据集,除了鸟那一类是相同的类别,其他九个类别都不相同。这表明小样本学习并不希望模型学习到类别的特征,而是去学习如何更好的区分类别与类别之间的不同。
在这个阶段中,支持集就可以看做普通机器学习中的训练集,用于模型的训练,而查询集就可以看作是测试集,用于判断模型是否训练到最优
得到训练过的模型以后,进入第二个阶段,称为元测试。首先使用元测试的支持集上训练模型,让模型对该数据集进行一定的微调,让这个模型更好的适应这个元测试阶段的数据集,然后在查询集上运行,查看测试结果。
基于度量的方法,代表模型为prototypical net[1]和matching net[2]。
这个方法和我们做嵌入的方法很像,就是通过距离来判断类别。通过计算支持集和查询集的相似度,来学习embedding函数。如图所示,
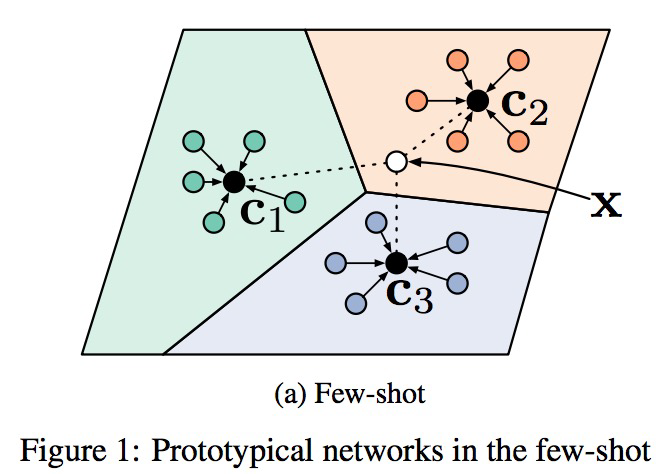
公式为\(\mathbf{c}_{k}=\frac{1}{\left|S_{k}\right|} \sum_{\left(\mathbf{x}_{i}, y_{i}\right) \in S_{k}} f_{\phi}\left(\mathbf{x}_{i}\right)\),嵌入函数即为\(f_{\phi}(xi)\),大致是说对于每个类别,取这个类别中所有embedding的平均作为这个类的embedding,称为ck。然后对于一个查询集中的点,输入\(f_{\phi}(xi)\)得到embedding,计算和各个ck之间的距离,来判断是哪个类别。
基于梯度的方法,有时候也被称为基于优化的方法,代表作为MAML[3]。
如下图所示:
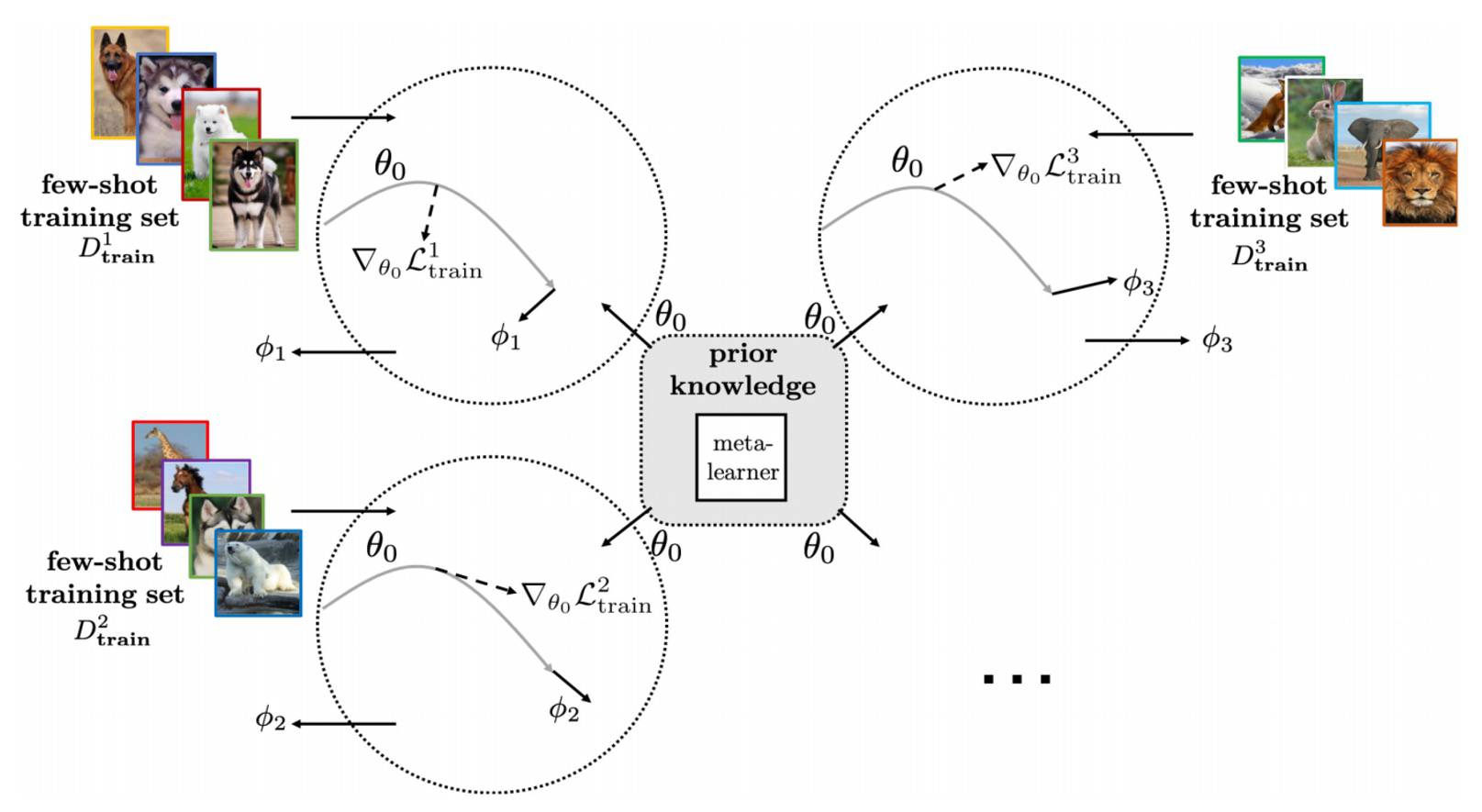
对于这个模型,初始化一个参数θ。在meta training的过程中,对于每个类别,在优化过程中会学习到自己的参数φ。会有各自自己的优化过程。那么通过优化过程平均这个φ,作为meta-testing的初始化。这样一个初始化的参数在学习新的support set时就会学的非常快。
本文来自AAAI2020,文章题目叫通过知识迁移的图小样本学习,张初旭老师为本文的第二作者。
和其他图表示学习工作一样,图的小样本学习也分三个类别,即节点级别的,边级别的,图级别的。本文为节点级别的小样本学习。
所有其他领域的方法要迁移到图领域往往会面临一个问题,图特有的数据形式,使得它不只有每个节点自身的特征,还有节点与节点之间的结构关系,如何处理这种结构关系就是将方法应用到图领域的关键。
首先,在meta training的阶段,我们拥有几张小样本训练图,可能一张图上有几个类别,每个类别有个位数到十位数左右的节点,例如图上左边的那个子图。
目标是,通过meta training得到的模型,在meta testing阶段,通过少数几个支持集的样本对模型参数进行一定的调整,来预测查询集中的标签。
它的idea是,通过补充图、补充类上训练的模型,进行知识迁移,来提取出一种元知识。所谓的知识迁移,就是指的在元训练阶段和元测试阶段所使用的完全不同的数据集,用别的数据集训练出来的模型做本数据集的任务,就可以叫知识迁移。
这里所谓的补充图,补充类,就是前文小样本学习中提到的补充集。第一张图中有T1,T2,一个T就是一个补充集,放到图上,对于节点分类任务,一个图就是一个数据集,所以称之为补充图。
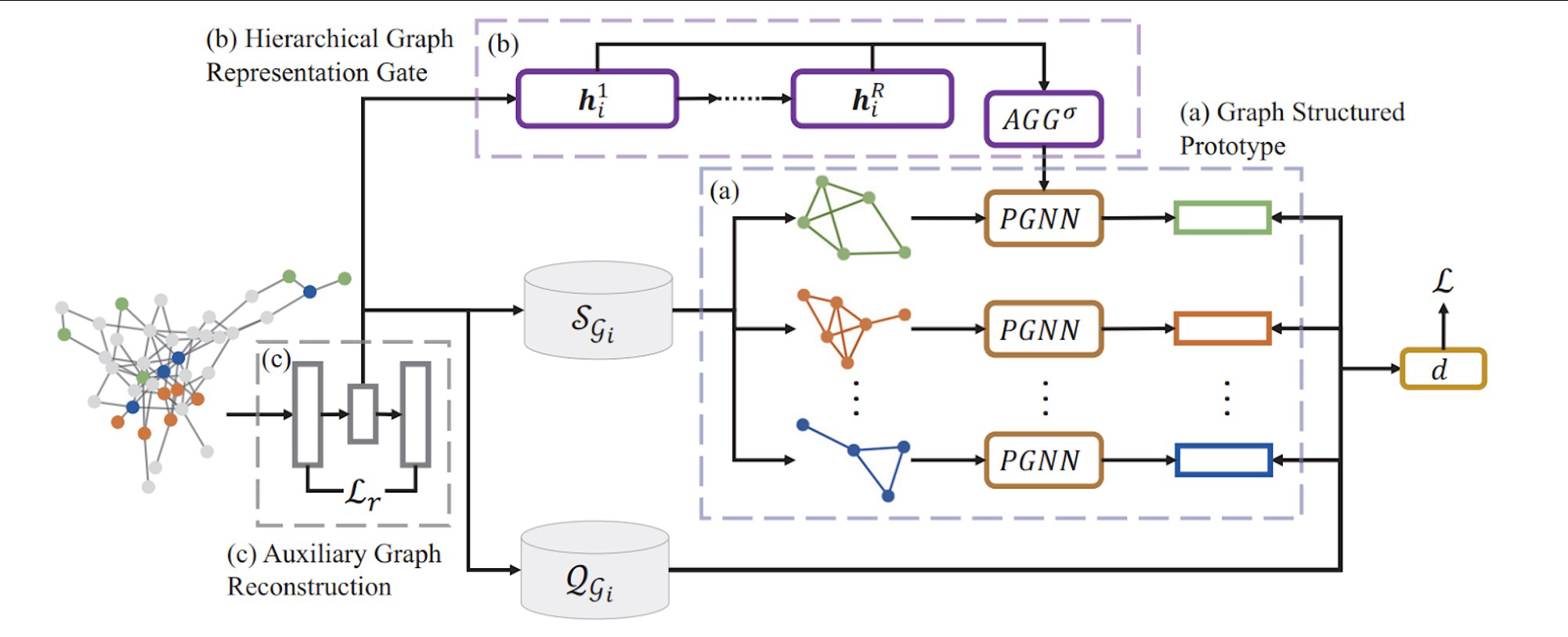
本文的模型架构具体来说分为三个模块
对一张图,使用GNN生成各个节点之间的embedding,然后可以直接使用prototypical net的方法,计算个点之间的距离。即每个点的embedding就是一个1*多少多少维的向量,可以根据类别,直接生成每个每个类别的embedding,然后计算查询集之中的embedding和每个类别的embedding之间的距离,也就是这个损失函数。
这就是第0步,啥都不用,直接使用prototypical net,直接生成embedding。
step a上面的第零步这种情况,就是没有考虑图的结构信息,只使用了每个节点的embedding,为了利用图的结构信息,作者首先增加了a模块,称作图结构原型(graph structure prototype)。
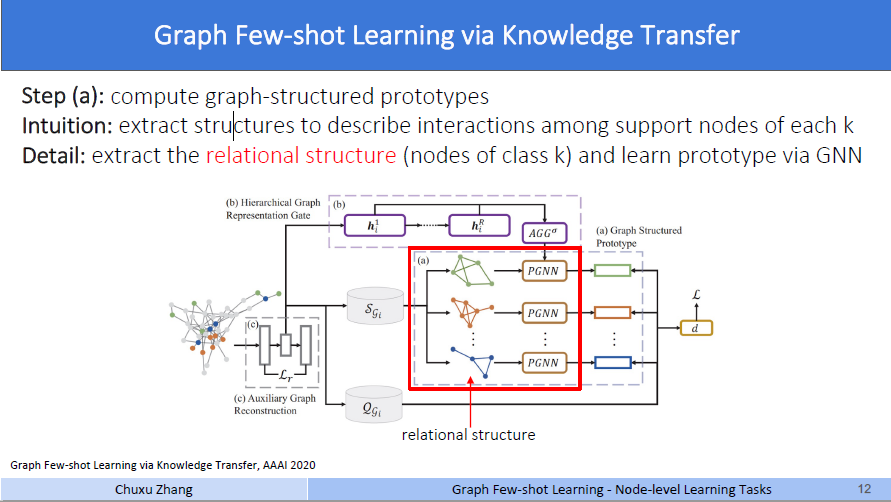
它说,第a步用来计算图结构原型。思想是对每一个类别的支持集节点,提取结构来描述交互作用。
作者在研究如何保留图的结构信息时,做出了一个理论上的假设。详情见论文4.1小节开头,在作者说,在绝大多数情况下,图上的节点有两个重要的角色。一是和类别可能不同的邻居节点的局部交互,二是和距离很远的相同类别的节点的交互,这种交互可以被全局查看,这也就是作者所认为的“全局结构信息”。那么对于第一种作用,就是上面提到的用GNN生成embedding,这个过程就是和邻居节点通过消息传播做聚合的过程,可以体现出和不同类别邻居节点的局部交互。对于第二点,作者说(见图上detail的部分),提取第k类节点的关系结构,通过GNN学习原型。
具体做法是,通过某些相似性度量方法,将一张图拆分成k个子图,每个子图包括这个类别的全部节点。这里说的相似性度量,文章中提到,是两个节点k跳中相同邻居的数量,或者是节点间的逆拓扑距离。
就以图上这个蓝色的类为例,可以看到这三个节点非常的近,它们k跳的相同邻居肯定很多,那么就认为在子图的结构上,他们是相连的,而这个蓝色的点离这三个点非常的远,所以它只能和这三个点中最近的点有一个连接。(具体细节上这一块是个什么操作我并不很确定,可能需要看代码才能明白)
通过这样子对每个类别构建子图,作者说他捕获了每个类别的关系结构,然后将这每个子图都输入一个PGNN,原型图神经网络,在本文中,就是一个一层的GNN,可以对每个子图的embedding再做一次1跳的消息传播,得到新的embedding,然后做一个池化操作,生成这个类别的embedding ck,式子如下
\[\mathbf{c}_{i}^{k}=\operatorname{Pool}_{j=1}^{n_{i}^{k}}\left(\operatorname{PGNN}_{\phi}\left(\mathcal{R}_{i}^{k}, f_{\theta}\left(\mathcal{S}_{i}^{k}\right)\right)[j]\right) \]那么这样得到的embedding可以代表这个类别的信息。然后再拿查询集中的点的embedding和每个类别进行比较,和上文相同。只不过上文第0步这个ck是简单的取平均,而这边是使用PGNN生成的。
step b然后啊,这个step b模块,称之为分层图表示门控(Hierachical Graph Representation Gate)。这个分层图表示学习,是早期的一个文章[4],主要是用于图分类。图信息都是层级表示的,例如地图、概念图、流程图等,捕获层级信息将能更加完整高效地表示图。为什么作者要引入这个模块呢?因为在小样本学习中,不止这一张图。一个meta-training 的过程有很多张图,不同的图就会有不同的拓扑结构。对于这个HGR,具体内容如下
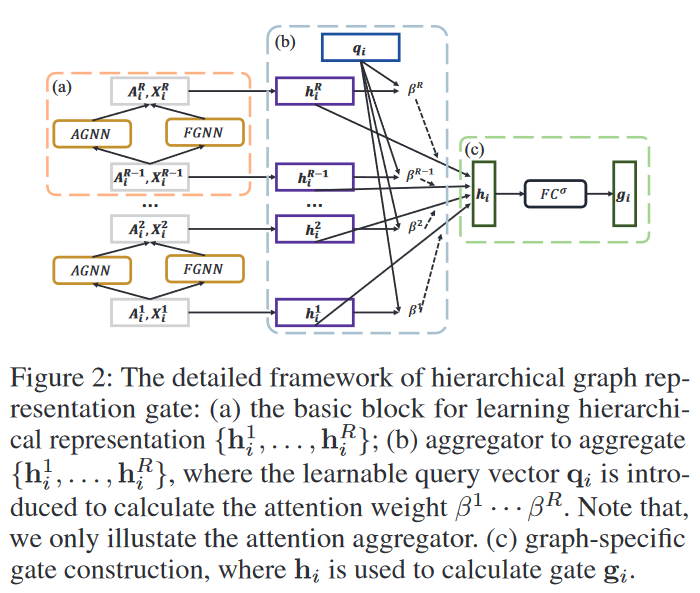
第一步,见橙色的区域a,学习分层图表示的基础模块。对于拿到手的一个邻接矩阵A和特征X,通过这个分层网络的两个步骤,AGNN和FGNN,对图进行分层,可以得到对应每一个层级的表示,或者说embedding。
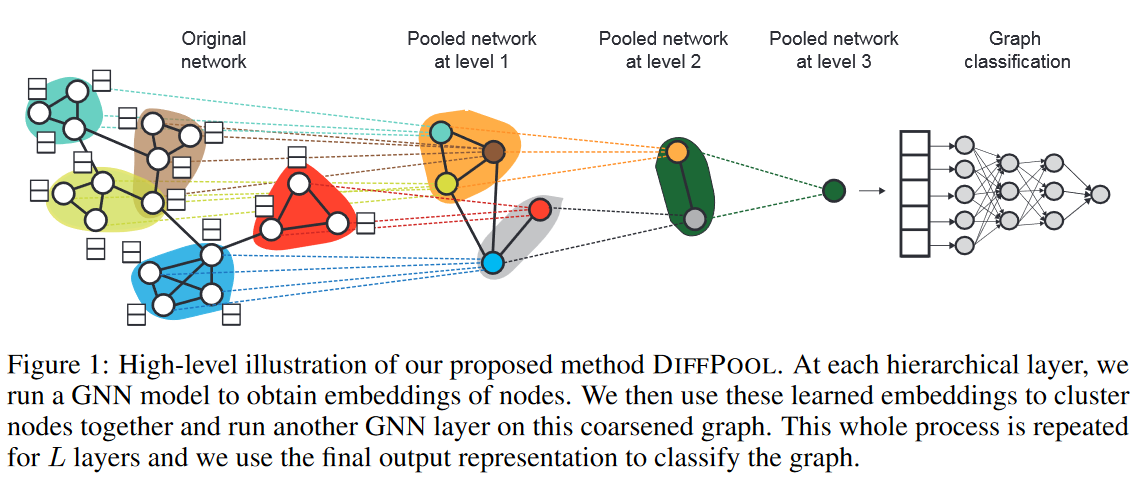
这一块有一个不是很确定的点,具体这个层级的意思。如图,每一个临近节点组成的一个小子图,可以看做一个层级。因为可以看到,图结构中的一个小子图,在第一个层级被聚合成了一个小簇,再到第二层又被聚合成了更小的簇,最后得到了一个嵌入,这个嵌入就可以视为这个图的拓扑信息,在图分类的领域中,这个向量在后续通过神经网络训练来实现图分类。
所以我们理解这个第一步的功能,就是得到图在图分类层面的表示,也就是每一个层级图的嵌入。
第二步,回到这个Fig2,见蓝色的区域b。在得到这个层级的特征表示后,做一个池化操作可以得到这个层级的图表示,对每个层级做这个操作以后,就得到了引入一个qi,可以认为是一种注意力机制,乘上每一个embedding做聚合,得到了这个图的嵌入表示hi。那么这个hi,作者就认为,视作这个图结构的高度概括,是这张图的图表示。
第三步,见绿色的区域c。文中4.2节的最后一段说到,前人的研究表明,相似的图在GNN上会有相似的参数。所以作者引入了一个门控函数来弥补图的具体化信息。一般来说,遇到的所谓的门控,基本上都是矩阵的哈达玛积。先将hi放入一个可学习的线性层,\(\mathbf{g}_{i}=\mathcal{T}\left(\mathbf{h}_{i}\right)=\sigma\left(\mathbf{W}_{g} \mathbf{h}_{i}+\mathbf{b}_{g}\right)\),然后和上文中step a中的PGNN的参数做一次哈达玛积,也就是矩阵中对应位置的值做乘积。
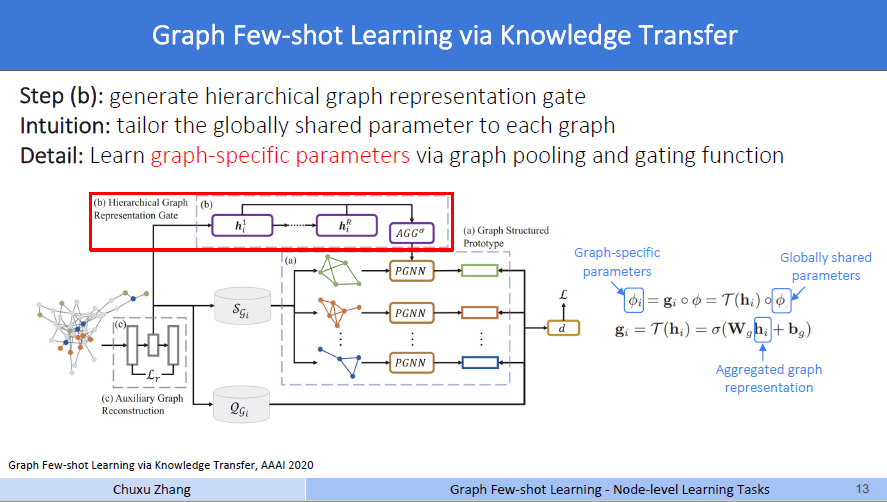
如图右边的公式所示啊,\(\phi\)就是step a中PGNN训练的参数,这里称为全局共享参数,一般来说就是一个权重矩阵。经过\(\phi_{i}=\mathbf{g}_{i} \circ \phi=\mathcal{T}\left(\mathbf{h}_{i}\right) \circ \phi\)后,得到的\(\phi_i\),称之为图具体参数,就是说这时候我的PGNN的参数,针对不同的数据集的补充图,做过不同的特化。
为什么有这个第三步呢,作者说,仅仅靠这个,非常遥远的这个匹配损失,来训练本身的节点表示,是非常非常困难的。第一步所使用的损失函数
\[\mathcal{L}_{i}^{k}=-\sum_{\left(\mathbf{x}_{i, j}^{q_{i}}, y_{i, j}^{q_{i}}\right) \in \mathcal{Q}_{i}^{k}} \log \frac{\exp \left(-d\left(f_{\theta}\left(\mathbf{A}, \mathbf{x}_{i, j}^{q_{i}}\right), \mathbf{c}_{i}^{k}\right)\right)}{\sum_{k^{\prime}} \exp \left(-d\left(f_{\theta}\left(\mathbf{A}, \mathbf{x}_{i, j}^{q_{i}}\right), \mathbf{c}_{i}^{k^{\prime}}\right)\right)}, \]同时负责了这个PGNN,这个HGRG,和原本的这个嵌入函数fθ的优化过程。估计是单靠这一个损失函数训练的效果不是很好,那么作者就说,在生成节点的embedding表示这一步,要新增一个新的限制,来控制这个原本的embedding节点的质量,称作补充图重构。
具体来说,用一个图的自编码器来重构这个图。增加了损失函数
Zi就是一个编码器,也就是一个GNN,生成图中每个节点的表示,然后通过一个解码器,在乘以其转置,得到的这个结果用于描述图的结构,和邻接矩阵相减做F范数。

这个损失函数的含义是,要求图的结构尽量的不变,然后得到正常的embedding。Intuition部分说这是一种自监督的方法,用自监督的重构损失来提高节点标识的质量。
这样,损失函数就变成了

最后是总体的算法:
- 初始化参数Θ,
- 采样一些图,得到领接矩阵和特征矩阵
- 对于每一个图,采样出支持集和查询集
- 计算embedding和重构损失Lr stepc中的内容
- 计算这个图的图表示,和参数φ做门控 stepb中的内容
- 构建关系图并计算图原型
- 计算图原型和查询集中embedding的距离,并构成损失函数Li
- 反向传播更新参数
在论文第五章节的右边部分,作者说到,他们沿用了传统的小样本学习设置。对于每一张图,每个类别中去N的带标签的节点来作为支持集,身下的节点都是用于评估表现的查询集,如下图。
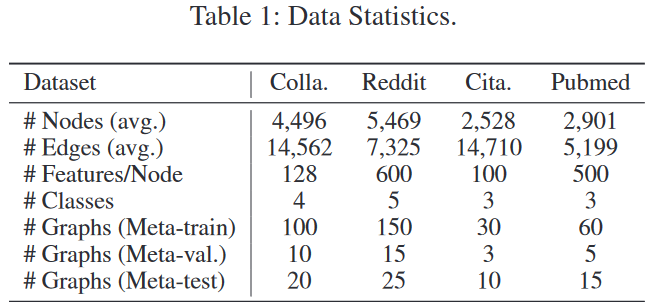
由于step b的分层网络有一个注意力机制qi,所以实验了使用mean和attention两种情况,称为GFL-mean和GFL-att。GFL-mean表示对hi的聚合采用的平均池化(论文中等式6),GFL-att表示对hi的聚合采用的注意力聚合(论文中等式7)。
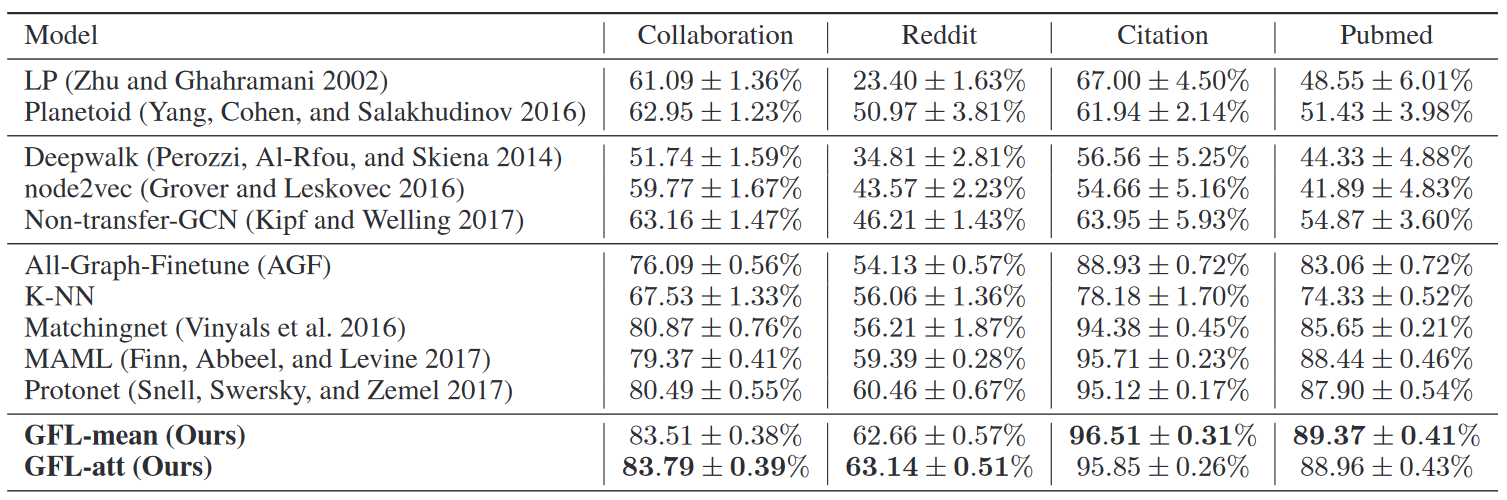
KNN往上都传统的图神经网络方法,可以看到效果都不咋样。在Meta-train阶段只有100多个甚至几十个节点训练出来的模型,在剩下的查询集上表现糟糕是理所应当的。
三种经典的小样本学习表现很好,说明即使没有考虑图的结构信息,全靠节点信息,小样本学习方法依旧可以奏效。
本文的方法在原本的小样本方法上更进一步,大概提升在二到三个点左右,可以看到这么复杂的结构还是有用的。
小样本学习有一种方法称作MAML,和我正在做的某个方法有一定相似之处,目前正在研究如何考虑结构信息,将原方法迁移到图上来。那么MAML乃至整个小样本学习迁移到图领域所做的方法,对我现在这个方法迁移到图上能有一定的参照。
引用文献:
[1] Snell J, Swersky K, Zemel R. Prototypical networks for few-shot learning[J]. Advances in neural information processing systems, 2017, 30.
[2] Vinyals O, Blundell C, Lillicrap T, et al. Matching networks for one shot learning[J]. Advances in neural information processing systems, 2016, 29.
[3] Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks[C]//International conference on machine learning. PMLR, 2017: 1126-1135.
[4] Ying Z, You J, Morris C, et al. Hierarchical graph representation learning with differentiable pooling[J]. Advances in neural information processing systems, 2018, 31.
