Homomorphic Evaluation of the AES Circuit：解读

之前看过一次，根本看不懂，现在隔这么久，再次阅读，希望有所收获！
论文版本：Homomorphic Evaluation of the AES Circuit(Updated Implementation)

• 首先明白AES电路是什么？
  暂且理解为AES加密算法，以电路的形式实现。

注：bootstrapping 自举；key switching 密钥交换； modulus switching 模交换

介绍

• 使用Leveled-FHE方案（BGV）加密和同态计算（不用自举），使用同态库（HElib）
• 使用SIMD编码技术
• 使用模交换和密钥交换技术改进版

AES电路

当对使用AES加密的数据进行计算时，AES同态解密就是将用AES加密的数据转换为用，FHE加密的数据，然后执行计算。

环表示 符号表示

• \([z]_q\)：整数\(z\)模\(q\)，范围在\((-q/2,q/2]\)

• \(m\)次分圆多项式：\(\Phi_m(X)\)，阶数为\(\phi(m)\)，即多项式的最高次幂为\(\phi(m)\)，例如\(\Phi_m(x)=(x-a_1)(x-a_2)...(x-a_{\phi(m)})\)，阶是\(\phi(m)\)

• 模\(q\)的多项式环：\(A_q=Z[X]/(\Phi_m(X))\) ，即整系数的多项式（模\(\Phi_m(x)\)和模\(q\)）集合，阶数为\(\phi(m)-1\)

多项式表示

一个\(m\)次分圆多项式\(\Phi_m(X)\)包含\(m\)次本原单位根\(\zeta\)，\(m\)次分圆多项式可以拆分为若干个多项式相乘，即\(\Phi_m(X)=\prod_{i}(X-\zeta ^i)(mod q)\)

m次本原单位根有\(\phi(m)\)个

给定一个多项式\(a\in A_q\)，有两种表示方法：：系数表示法（coefficient representations）和计算表示法（evaluation representation）

系数表示法

可以将\(a\)看作一个阶为\(\phi(m)-1\)的多项式，即\(a(X)=\sum_{i<\phi(m)}a_iX^i\)，列出所有的系数表示这个多项式，即\(a=<a_0,x_1,...,x_{\phi(m)-1}>\in (Z/qZ)^{\phi(m)}\)，这就是系数表示法

计算表示法

将\(m\)次本原单位根\(\zeta\)带入多项式\(a(X)\)，即\(b_i=a(\zeta ^i)\)，会得到\(\phi(m)\)长的向量，即\((b_0,b_1,...,b_{\phi(m)})\)，这就是计算表示法

转换

可以看出，这两种表示法是通过\(b=V_m.a\)转换的，其中\(V_m\)是一个基于\(m\)次本原单位根的范德蒙矩阵\((mod q)\)，即\((a(X) mod (X-\zeta ^i))=a(\zeta ^i)=b_i\)，因此用计算表示法的\(a\)是一个多项式的中国剩余定理的表示 (CRT表示法)。

上面是基于CRT实现的转换，还有其他的方法：牛顿插值法、拉格朗日插值法、**快速傅立叶变换（FFT）更多请参考：FFT

上面两种表示法，都可以将一个多项式\(a\in A_q\)表示为一个长\(\phi(m)\)的整数向量。如果\(q\)是一个"复合体"，这些整数每一个都可以用标准二进制编码（ standard binary encoding）或者用CRT（ Chinese-Remaindering）。我们一般在系数表示法中使用标准二进制编码，计算表示法中使用CRT。

所以后者也叫做双CRT表示（double CRT representation），对应于\(\Phi_m(X)\)和\(q\)所拆分的因子。

这里的\(q\)说是一个"复合体"，可以看作是一个很大的数

多项式计算

由于是基于多项式环上的计算，所以会有很多整数多项式间的计算。例如：模乘（modular multiplications），模加（modular additions）， Frobenius映射（用于快速计算次幂\(x^a\)）。

大部分的计算可以在计算表示法下进行，另外标准的模交换和密钥交换需要在系数表示法下进行【密文中的噪音在系数表示法很小，在计算表示法下则不会】，所以在整个过程中，多项式需要在这两种表示下来回转换，这是最耗时的！所以在该方案中，将始终将密文保持在计算表示下，仅当某些操作需要时才转换为系数表示，然后再转换回来。该方案中描述的密钥交换和模交换的变体是可以在计算表示法下执行的，密钥交换还有一个优点：密钥交换矩阵的尺寸减少，这是影响性能的重要因素。

由于转换耗费计算量，所以本文也是一直做优化，减少转换次数。

BGV基础方案

这里采用的是BGV变体方案[1]，密文和密钥都是在\(A\)上的向量，明文空间为\(A_2\)，密文空间\(A_q\)

密钥【current secret key s】和模数【current integer modulus q】会随着同态计算而变化（密钥交换和模交换导致的）

给定一个结构：密文\(c\)，对应的密钥\(s\)、模数为\(q\)、明文为\(a\)，则解密结构为:

\[a\leftarrow [[\left<c,s\right> mod \Phi_m(X)]_q]_2 \]

其中\([\left<c,s\right> mod \Phi_m(X)]_q\)叫做密文\(c\)的噪音，衡量噪音的大小用欧几里德范数，即噪音的大小为：

\[||[\left<c,s\right> mod \Phi_m(X)]_q||_2 \]

以下再提到范数，即欧几里德范数（\(l_2\)范数）

噪音需要足够小，这样密文才有效，所以噪音满足一定的界限。

这里的BGV方案提供5个同态计算：加法（ addition）、乘法（ multiplication）、"自同构"（automorphism）、密钥交换（key-switching）和模交换（modulus-switching）：

加法

密文+密文，具体来说：两个密文\(c_1,c_2\in A_q\)，对应的明文为\(a_1,a_2\in A_2\)，具有相同的密钥和模数\(q\)，相加后\(c_1+c_2\in A_q\)，对应的明文为\(a_1+a_2\in A_2\)。
相加后模数和密钥不变，噪音累加。

乘法

密文*密文(张量积)，具体来说，两个密文\(c_1,c_2\in A_q\)，对应的明文为\(a_1,a_2\in A_2\)，具有相同的密钥和模数\(q\)，相乘后\(c_1*c_2\in A_q\)，对应的明文为\(a_1*a_2\in A_2\)。
模数不变，密钥维数翻倍(\(n\)->\(n^2\))，噪音剧增。

密钥交换

需要密文的范数远小于\(q\)

转换密文的密钥，具体来说（密文，密钥，模数）：
\((c',s',q)\)->密钥交换->\((c,,s,q)\)

主要用作在密文*密文后，密钥的维数增长，这时需要使用密钥交换，把密钥的维数降下去。假设\(s'\)的维数为\(n^2\)，\(s\)的维数为\(n\)。

进行密钥交换，需要一个交换矩阵\(W=W[s\to s]\in A_q\)，\(W\)的第\(i\)列近似表示为\(s'\)的第\(i\)个元素的加密。"近似"转换：\(c=W.c'\) ，例如：
\(s\)的第\(i\)个元素为\(s_i' \in A\)（范数远小于\(q\)），\(W\)的第\(i\)列为一个\(n\)维向量\(w_i\)，则

\[[<w_i,s>mod \Phi_m(X))]_q=2e_i+s_i' \]

其中，\(e_i\)的范数很低，那么对于\(e=(e_1,e_2,..,e_{n'})\)，有\(sW=s'+2e \in A_q\)，对于任意的密文\(c'\)，设\(c=W.c'\in A_q\)，则有：

\[[<c,s>mod\Phi_m(X))]_q=[sWc'mod\Phi_m(X)]_q=[<c',s'>+2<c',e>mod \Phi_m(X)]_q \]

可以看出，由于\([<c',s'>mod \Phi_m(X)]_q\)的范数远小于\(q\)，而且\(e\)的范数远小于\(q\)，故$$[[<c,s>mod\Phi_m(X))]_q]_2=[[<c',s'>mod \Phi_m(X)]_q]_2$$

总的来说，密钥交换改变了密钥，模数没有改变，噪音增加了\(2||<c',e>||_2\)。

模交换

模交换用来减少噪音的范数，具体来说（密文，密钥，模数）：
\((c,s,q)\)->模交换->\((c',,s,q')\)

其中，新模数\(q'\)给定，\(c'=c.q'/q\)，\(c\)乘以\(q'/q\)，得到了一个"分数密文"，然后通过四舍五入得到整数密文\(c'\)。模交换需要满足两个前提条件：

• \(c'=c (mod 2)\)
• 四舍五入产生的噪音范数很小，即\(\tau \overset{def}{\leftarrow} c'-(q'/q)c\)的范数很小

\(c\)和\(c'\)的转换是用系数表示法，只要密钥\(s\)的范数足够小和\(q'<<q\)，则噪音的大小就可以降低！

因为模数改变，所以BGV方案需要提前准备"一串"模数，即模数链（chain of moduli），\(q_0<q_1<...<q_{L-1}\)，从小到大，\(L\)为方案的级数（层数），对于"新鲜密文"对应的模数为\(q_{L-1}\)，即最大。

同态计算（一般指乘法）后密文的噪音过大，需要执行模交换将模数从\(q_i\)转换为\(q_{i-1}\)，噪音降低。直到模数为\(q_0\)，就不能进行同态计算了，所以才叫做有限级数的FHE（Leveled-FHE）。

自同构

定义一种映射:

\[\kappa _i:a\to a^{(i)} \]

使得\(a(X)\in A\)转换为\(a^{(i)}(X)\overset{def}{\leftarrow}a(X^i) mod \Phi_m(X)\)

也是一种对密文的运算，具体来说（密文，密钥，明文）：
\((c,s,a)\)->自同构->\((c^{(i)},s^{(i)},a^{(i)})\)

具体没看懂，涉及到伽罗瓦群的概念，后面补充

打包密文

明文空间:\(A_2\)可以看作是一个"plaintext slots"向量，具体说：若分圆多项式\(\Phi_m(X)\)能拆分为\(l\)个不可约多项式的乘积，即\(\Phi_m(X)=\prod_{j=}^{l-1}F_j(X)(mod 2)\)，则一个明文\(a(X)\in A_2\)可以被看作是\(l\)个小多项式的编码而成，即\(a_j(X)=a(X) mod F_j(X)\)，这里的\(a_j(X) mod F_j(X)\)是一个slot，因此我们可以用它表示扩域\(GF(2^d)\)上的一些元素。

为什么可以表示，或许是扩域的性质吧

附录 明文槽(plaintest slot)

多项式环：\(A=Z[X]/\Phi_m(X)\)
明文空间：\(A_2\)
密文空间：\(A_q\)
分圆多项式\(\Phi_m(X)\)可以分为\(l\)个不可约多项式的乘积，即\(\Phi_m(X)=F_1(X).F_2(X)....F_l(X) (mod 2)\)，其中\(F_i(X)\)的最大阶数为\(d=\phi(m)/l\)，每一个\(F_i(X)\)对应一个"plaintest slot"，所以\(a\in A_2\)可以表示为一个\(l\)长的向量\((a mod F_i(X))_{i=1}^l\)

伽罗瓦群\(Gal=Gal(Q(\zeta _m)/Q)\)包含一个映射:

\[\kappa _k:a(X)\to a(x^k)mod\Phi_m(X) \]

并且\(a(x^k)\)与\((Z/mZ)^*\)同构。

等学完伽罗瓦群后再回看

标准嵌入范数（Canonical embedding norm） 双CRT表示（Double CRT）

分圆多项式\(\Phi_m(X)\)包含m次本原根，可以分为本原根的乘积：\(\Phi_m(X)=\prod_{i\in(Z/mZ)^*}(X-\zeta ^j)(mod q)\);
模数\(q\)可以拆分为多个素数相乘\(q=\prod_{i=0}^{t}p_i\);
所以一个密文\(a\in A_q\)可以表示为一个\((t+1)*\phi(m)\)的矩阵（以\(\Phi_m(X)mod p_i\)包含m次本原根为元素），即：

\[dble-CRT^t(a)=(a(\zeta ^j )mod p_i)_{0\leq i\leq t,j\in \phi(m)} \]

其中，这种表示法可以用\(t+1\)次FFT算法(模 \(p_j\))，如下：

一次FFT，可将一个多项式"解码为"一组数（向量）编码；而逆操作，则需\(t+1\)次IFFT算法(模 $\Phi_m(X) $模 \(p_j\))，如下：

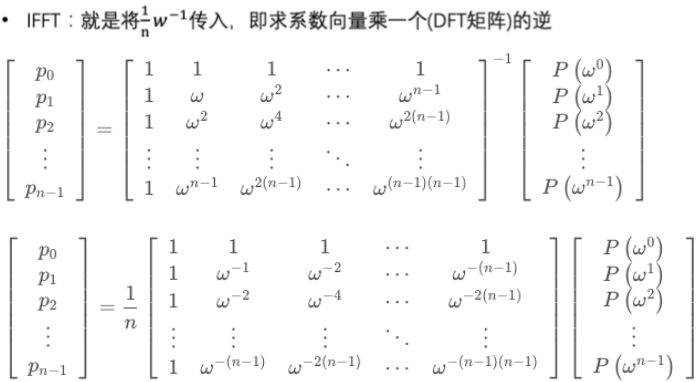
一次IFFT，可以将一组数（向量）"编码为"一个多项式

这种表示法也具有同态乘法和加法：

参考

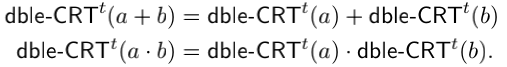
1、Fully Homomorphic Encryption with Polylog Overhead