假设通过用户 - 物品相似度进行个性化推荐
用户和物品的 Embedding 都在一个 \(k\) 维的 Embedding 空间中,物品总数为 \(n\),计算一个用户和所有物品向量相似度的时间复杂度是$ O(k*n)$
直觉的解决方案- 基于聚类
- 基于索引
优点:
离线计算好每个 Embedding 向量的类别,在线上我们只需要在同一个类别内的 Embedding 向量中搜索就可以。
缺点:
-
存在着一些边界情况,比如,聚类边缘的点的最近邻往往会包括相邻聚类的点,如果我们只在类别内搜索,就会遗漏这些近似点
-
中心点的数量 k 也不那么好确定,k 选得太大,离线迭代的过程就会非常慢,k 选得太小,在线搜索的范围还是很大
Kd-tree(K-dimension tree)
首先,构建索引,然后用二叉树搜索
比如,希望找到点 q 的 m 个邻接点,我们就可以先搜索它相邻子树下的点,如果数量不够,我们可以向上回退一个层级,搜索它父片区下的其他点,直到数量凑够 m 个为止
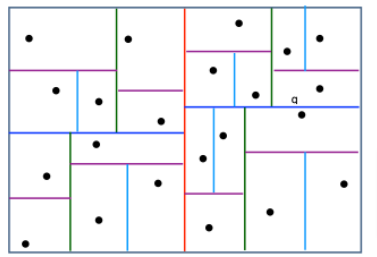
缺点:
- 无法完全解决边缘点最近邻的问题。对于点 q 来说,它的邻接片区是右上角的片区,但是它的最近邻点却是深蓝色切分线下方的那个点。
局部敏感哈希的基本思想是希望让相邻的点落入同一个“桶”,这样在进行最近邻搜索时,我们仅需要在一个桶内,或相邻几个桶内的元素中进行搜索即可。如果保持每个桶中的元素个数在一个常数附近,我们就可以把最近邻搜索的时间复杂度降低到常数级别。
把二维空间中的点通过不同角度映射到 a、b、c 这三个一维空间时,可以看到原本相近的点,在一维空间中都保持着相近的距离。而原本远离的绿色点和红色点在一维空间 a 中处于接近的位置,却在空间 b 中处于远离的位置。

欧式空间中,将高维空间的点映射到低维空间,原本接近的点在低维空间中肯定依然接近,但原本远离的点则有一定概率变成接近的点
内积相似度是经常使用的相似度度量方法,还有曼哈顿距离,切比雪夫距离,汉明距离 等。假如 用内积操作来构建局部敏感哈希桶
假设 \(v\) 是高维空间中的 $k $ 维 Embedding 向量,$x $ 是随机生成的 \(k\) 维映射向量。那我们利用内积操作可以将 $ v $ 映射到一维空间,得到数值$ h(v)=v⋅x$。
使用哈希函数 \(h(v)\) 进行分桶,公式为:$h^{x,b}(v)= ⌊\frac{x⋅v+b}{w}⌋ $ 。其中, \(⌊⌋\) 是向下取整操作, \(w\) 是分桶宽度,\(b\) 是 \(0\) 到 \(w\) 间的一个均匀分布随机变量,避免分桶边界固化。
防止相邻的点每次都落在不同的桶
如果总是固定边界,很容易让边界两边非常接近的点总是被分到两个桶里。这是我们不想看到的。 所以随机调整b,生成多个hash函数,并且采用或的方式组合,就可以一定程度避免这些边界点的问题。
采用 m 个哈希函数同时进行分桶。如果两个点同时掉进了 m 个桶,那它们是相似点的概率将大大增加。
用几个hash函数?怎么组合多个hash函数?
多桶策略关于怎么组合多个hash函数,没有固定做法,可以用不同的组合策略.
-
点数越多,我们越应该增加每个分桶函数中桶的个数;相反,点数越少,我们越应该减少桶的个数;
-
Embedding 向量的维度越大,我们越应该增加哈希函数的数量,尽量采用且的方式作为多桶策略;相反,Embedding 向量维度越小,我们越应该减少哈希函数的数量,多采用或的方式作为分桶策略。
局部敏感哈希实践一些经验值设定
每个桶取多少点跟线上想寻找top N的规模有关系。比如召回层想召回1000个物品,那么N就是1000,那么桶内点数的规模就维持在1000-5000的级别是比较合适的
Embedding在实践中超过100维后,增加维度的作用就没那么明显了,通常取10-50维就足够了
hash函数数量的初始判断,有个经验公式:Embedding维数开4次方。后续,调参按照2的倍数进行调整,例如:2,4,8,16
基于spark BucketedRandomProjectionLSH
def embeddingLSH(spark:SparkSession, movieEmbMap:Map[String, Array[Float]]): Unit ={
//将电影embedding数据转换成dense Vector的形式,便于之后处理
val movieEmbSeq = movieEmbMap.toSeq.map(item => (item._1, Vectors.dense(item._2.map(f => f.toDouble))))
val movieEmbDF = spark.createDataFrame(movieEmbSeq).toDF("movieId", "emb")
//利用Spark MLlib创建LSH分桶模型
val bucketProjectionLSH = new BucketedRandomProjectionLSH()
.setBucketLength(0.1)
.setNumHashTables(3)
.setInputCol("emb")
.setOutputCol("bucketId")
//训练LSH分桶模型
val bucketModel = bucketProjectionLSH.fit(movieEmbDF)
//进行分桶
val embBucketResult = bucketModel.transform(movieEmbDF)
//打印分桶结果
println("movieId, emb, bucketId schema:")
embBucketResult.printSchema()
println("movieId, emb, bucketId data result:")
embBucketResult.show(10, truncate = false)
//尝试对一个示例Embedding查找最近邻
println("Approximately searching for 5 nearest neighbors of the sample embedding:")
val sampleEmb = Vectors.dense(0.795,0.583,1.120,0.850,0.174,-0.839,-0.0633,0.249,0.673,-0.237)
bucketModel.approxNearestNeighbors(movieEmbDF, sampleEmb, 5).show(truncate = false)
}
refenences:
【1】王喆. 深度学习推荐系统
【2】Facebook 最近邻搜索库 FAISS
