有序的数组可以使用二分查找的方法快速检索一个数据,但是链表没有办法使用二分查找。
对于一个单向链表来说,即使链表中存储的是有序的数据,但如果想要从中查找某个数据时,也只能从头到尾遍历链表,其时间复杂度是 \(O(n)\)。
为了提高链表的查询效率,使其支持类似“二分查找”的方法,对链表进行多层次扩展,这样的数据结构就是跳表。跳表对标的是平衡树,是一种提升链表插入、删除、搜索效率的数据结构。
首先,跳表处理的是有序的链表,一般使用双向链表更加方便。
然后,每两个结点提取一个结点到上一级,提取的这一层被称作为索引层。
这时候,当想要查找 19 这个数字,可以先从索引层开始查找;当到达 17 时,发现下一个结点存储 21 这个数字,则可以确定,想要查找的 19 肯定是在 17 到 21 之间;这时候可以转到下一层(原始链表)中查找,快速从 17 开始检索,很快就可以查找出 19 这个数字。
加入一层索引之后,查找一个结点需要遍历的结点个数减少了,也就是查找效率提高了。实际上,一般会新增多层索引,拥有多层索引的跳表,查找一个结点需要遍历的结点个数将再次减少。
这种链表加多层索引的结构,就是跳表。
效率分析为了方便对跳表的效率做分析,在这里设定一个常见的跳表类型。
假设每两个结点会抽出一个结点作为上一级索引的结点,那第一级的索引个数大约就是 \(\frac{n}{2}\),第二级的索引个数大约就是 \(\frac{n}{4}\),以此类推,第 k 个索引的结点个数是第 k-1 个索引的结点个数的 \(\frac{1}{2}\),那么,第 k 个索引的结点个数就是 \(\frac{n}{2^k}\)。
时间复杂度假设索引总共有 h 级,最高级的索引有 2 个结点,使用公式 \(\frac{n}{2^h} = 2\) 进行反推,可以计算得出 \(h = \log_2 n - 1\),如果是包含原始链表那一级,跳表的高度就是 \(\log_2 n\) 级。
如果想要从跳表中查询某个数据时,每层都会遍历 m 个结点,那么,在跳表中查询一个数据的时间复杂度就是 \(O(m \log n)\)。
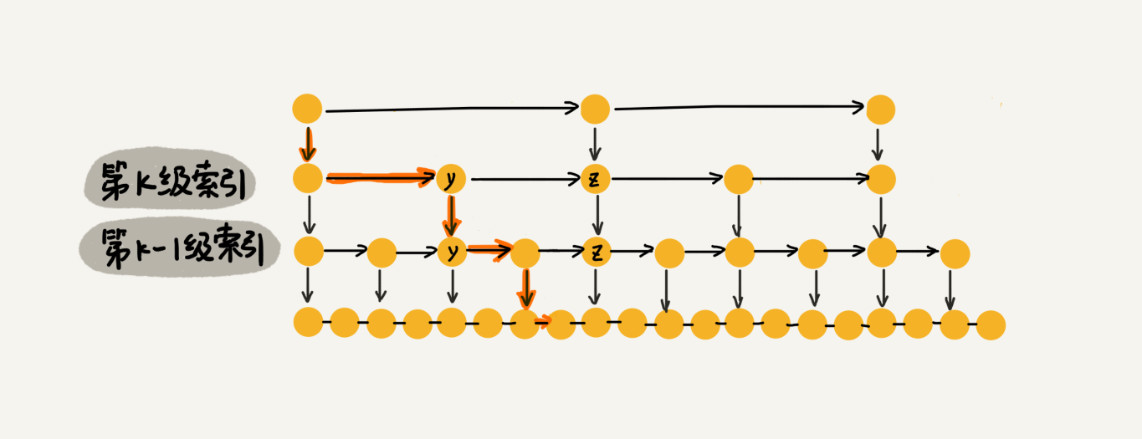
从上面图中可知,在每一级索引中最多只需要遍历 3 个结点,其实就可以看作是 m = 3。
实际就是,在最高级索引时最多遍历 3 个结点,当需要在下一级索引中继续检索时,算上前后两个当做范围的结点也只有 3 个,因此,在每一级索引最多只需要遍历 3 个结点。
如果细究的话,m 的值与抽取索引值的间隔有直接关系,但是只是计算时间复杂度的话,可以将 m 值看作是一个常数。
因此,在跳表中做检索的时间复杂度是 \(O(\log n)\)。
空间复杂度同样的,假设每两个结点会抽出一个结点作为上一级索引的结点,那第一级的索引个数大约就是 \(\frac{n}{2}\),第二级的索引个数大约就是 \(\frac{n}{4}\),依次类推,最终索引占用的空间将是 \(\frac{n}{2} + \frac{n}{4} + ... + 4 + 2 = n - 2\)。
所以,跳表的空间复杂度是 \(O(n)\)。
实际上,跳表是一种使用空间换时间的数据结构,以增加索引的方式,提高检索数据的效率。因此,跳表会比普通链表耗费更多内存进行数据存储。
结点间隔在上述分析跳表的时间复杂度和空间复杂度时,都是以每两个结点抽出一个结点作为上一级索引的结点。
实际上,也可以使用 3 个结点或 4 个结点甚至更多结点做间隔。当然,以不同个数结点做间隔时,检索效率和内存占用都会有些不一样。
假设以 3 个结点做间隔,占用的空间会有所降低,在这个跳表上做检索操作时,检索的效率也会有一些降低。
因为在每一级索引检索的最多结点个数将从 2 个变成 3 个,跳表的高度是 \(\log_3 n\) 级,最终占用的空间将是 \(\frac{n}{3} + \frac{n}{9} + ... + 3 + 1 = \frac{n}{2}\)。
在理论上,以 3 个结点做间隔的跳表与以 2 个结点做间隔的跳表的时间复杂度和空间复杂度都是一样的。但是,实际操作时,以 3 个结点做间隔的跳表的空间占用会比以 2 个结点做间隔的跳表更优一些。
实际上,在软件开发中,不必太在意索引占用的额外空间。虽然原始链表中存储的有可能是很大的对象,但索引结点可以只存储关键值和几个指针,并不需要存储对象,所以当对象比索引结点大很多时,那索引占用的额外空间就可以忽略了。
动态插入和删除上面理解的跳表都是静态的,实际开发中,跳表在新增、删除结点时需要做动态处理,否则容易导致检索效率降低。
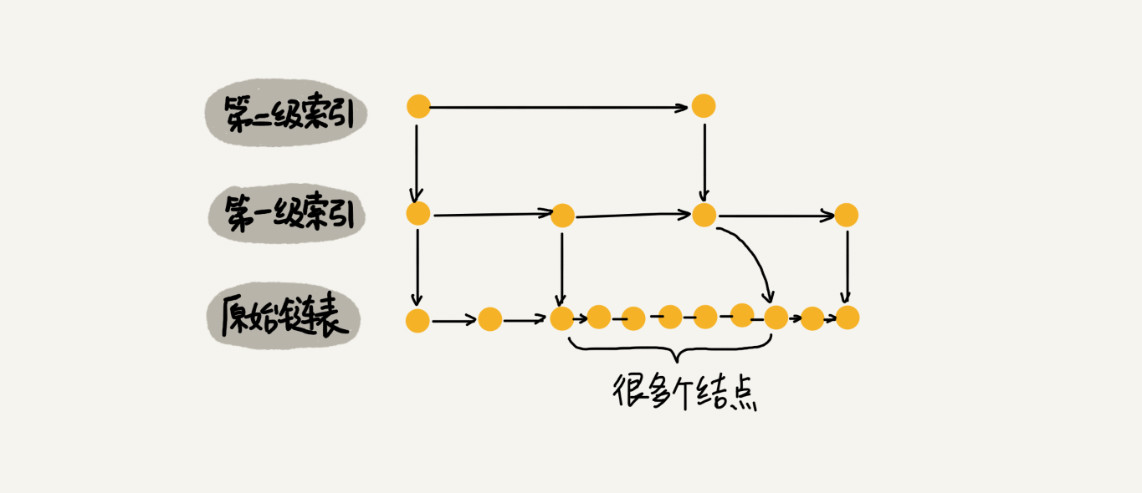
如上图所示,如果频繁插入结点,而没有对索引层做动态处理,很容易出现不满足一开始设定的跳表规则。
删除链表的结点时也是同样道理,如果删除结点而没有更新索引层,索引层容易出现已被删除的脏结点。
重建索引比较容易理解的方法就是重建索引,当每次插入、删除结点的时候,把整个跳表的所有索引层删除重建。
但是这种方法会降低插入结点时的效率,已知跳表的空间复杂度是 \(O(n)\),也可以推断出重建跳表索引层的时间复杂至少是 \(O(n)\)。
也就是说,使用重建索引的方式,跳表插入结点耗费时间将会直线上升。
随机索引与重建索引相比,随机索引的效率会更高一些,像 Redis 实现 SortedSet 底层用的跳表就是使用随机索引的方式进行动态处理。
这里的做法是通过使用一个随机函数,来决定这个结点插入时,是否需要插入到索引层、以及插入到第几级索引。
一般来说,通过随机函数得到的数据都是比较均匀的,也表示最终得到的跳表索引层也是比较均匀,而且数据量越大,索引层越是均匀。
先设定索引的生成规则:从原始链表中随机选择 \(\frac{1}{2}\) 个结点作为一级索引,从一级索引中随机选择 \(\frac{1}{4}\) 个结点作为二级索引,以此类推,一直到最顶层索引。这时候就需要根据这个规则完成所需的随机函数,并且是每次插入结点的时候,都通过随机函数判断这个结点需要插入到几级索引。
以下是 Redis 源码当中使用到的随机函数:
/* Returns a random level for the new skiplist node we are going to create.
* The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
* (both inclusive), with a powerlaw-alike distribution where higher
* levels are less likely to be returned. */
int zslRandomLevel(void) {
int level = 1;
while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
level += 1;
return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
这个随机函数会随机生成 1 到索引最高层数之间的一个数字,该方法有 \(\frac{1}{2}\) 的概率返回 1、有 \(\frac{1}{4}\) 的概率返回 2、有 \(\frac{1}{8}\) 的概率返回 3、以此类推。其中 1 表示不需要生成索引,2 表示需要生成一级索引,3 表示需要生成二级索引,以此类推。
为什么不是返回 1 时生成一级索引呢?这是因为,在生成比一级索引更高层级的索引时,都会向下生成索引,即如果随机函数返回 3,则会给这个结点同时生成二级索引和一级索引。这样,如果返回 1 时生成一级索引则会出现生成一级索引的概率为 100%。
使用随机索引方法的跳表,插入结点的时间复杂度与跳表索引的高度相同,最终时间复杂度降到 \(O(\log n)\),而不是重建索引的 \(O(n)\)。
应用场景 跳表和平衡查找树与平衡查找树相比,跳表拥有以下优势:
- 跳表的底层原始链表支持范围查询
- 跳表相对简单,更容易使用代码实现
- 跳表更加灵活,可以通过改变索引构建策略,有效平衡执行效率和内存消耗
针对上述的第 1 点,支持范围查询的 B+ 树更适用于磁盘,跳表主要用于内存中读取数据。
LSM-TreeLSM-Tree 全称是 Log Structured-Merge Tree,其中文名是日志结构的合并树,是一种分层的、有序的、基于硬盘的数据结构。
LSM-Tree 的核心思路是,首先写入数据到内存中,不需要每次有数据更新时就必须将数据写入到磁盘中,内存达到阈值之后,再使用归并排序的方式将内存中的数据合并追加到磁盘队尾。
因为跳表恰好就是天然有序的,所以在 flush 的时候效率很高,通常基于 LSM-Tree 结构的数据库在内存部分都会选择跳表这种数据结构。
HBase 的 MemStore 内部基于 LSM-Tree 实现,Google 开源的 LevelDB 以及 Facebook 基于 LevelDB 优化的 RocksDB 内部的 MemTable 都是基于 LSM-Tree 实现,它们都使用到了跳表这一结构。
本文原创首发于翔仔的技术博客,可点击跳转查看。




