前言:
广州疫情最近有点严重,回不去学校了。在家连不上系统,于是梳理一下学过的数学内容。大概有20章,尽量做到每天更新。
格式约定:
这是正文。
这是引用,导言或注释
斜体只是调侃,没有实际意义
数
从远古时代人们就发明了“数”的概念,主要用于计数。
什么是“数”?为什么 \(1+1=2\)?这是如何定义出来的?
简单来说,数是一种算术对象。确定的运算的对象构成的集合称为数集,数集中的元素称为数(numbers)。
我们可以用字母来表示一个数(已知的或未知的、变量或常量),例如
\[a,b,x,y,z \]都可以是数。
加法加法是定义的产物。一加一之所以等于二,不是因为一个苹果和一个苹果得到两个苹果,而是因为定义如此。
数学就像一种宗教,而非科学。你输入两个数,把它们相加,然后你就得到了一个全新的数,这就像魔法——你要么全信,要么全不信。
加法是一种二元运算(binary operator),也就是说加法运算接受两个数作为输入(input),得到一个数作为输出(outout)。书写上,我们在输入的两个数之间用加号(plus notation)连接。因此抽象的加法就是
\[a+b=c \]加法单位元\(0\) 是如何定义的?
进行加法运算时,我们注意到有一类数 \(x\),使得
\[a+x=a \]即(通俗的说)这个数加别的数等于那个数。我们把这样的 \(x\) 称为加法单位元,记作 \(0\)。
由此我们定义了 \(0\),数轴的原点被确定了。
搞这么复杂,你是法国小学生吗?学这些对搬砖有什么价值?
乘法乘法拥有巧妙的组合意义,比如 \(3\) 乘 \(5\) 是 \(5\) 个 \(3\) 相加。这也是我们小学定义乘法的唯一目的。
但组合意义是乘法的本质吗?如果不是,又该如何定义乘法?
乘法是一种二元运算,接受两个数作为输入,得到一个数作为输出。书写上,我们在输入的两个数之间用空格(空格在不产生歧义的情况下可以省略)连接。因此抽象的乘法就是
\[ab=c \]乘法单位元使用何种乘号?
一般而言,乘法的书写有三种:\(a\times b\),\(a\cdot b\) 和 \(ab\)。
在表达两个数(标量)相乘时,我建议使用第三种,因为叉乘记号(cross product notation,\(\times\))和点乘记号(dot probduct notation,\(\cdot\)),在向量运算时已经有明确的(不同的)含义了。
因此以后我们统一使用空格作为标量乘法的记号,例如三乘以五记作 \(3\ 5=15\),手写时可以使用 \(3(5)=15\)。
什么是 \(1\)?什么是 \(2\)?自然数是如何被定义的?
进行乘法运算时,我们注意到有一类数 \(x\),使得
\[ax=a \]即(通俗的说)这个数乘别的数等于那个数。我们把这样的 \(x\) 称为乘法单位元,记作 \(1\)。
由此我们定义了 \(1\),数轴的原点被确定了。
所以搞了半天你连 \(1,2,3,\cdots\) 这些最基本的算术单元都没有说吗?
自然数我们费尽心机终于定义了两个数(\(0,1\)),可是还有无穷无尽的数没有定义呢!
自然数集(记作 \(\mathbb{N}\))是由皮诺亚公理定义的集合,这一般是算术学家(你说的这个算术学家,是指小学生吗?)接触的第一个数集。
皮诺亚公理(简化版)
- \(0\) 是一个自然数。
- 如果 \(a\) 是一个自然数,则 \(a+1\) 也是一个自然数,称之为 \(a\) 的后继数。即 \(\forall_{a\in \mathbb{N}}a+1\in\mathbb{N}\)
- \(0\) 不是任何数的后继数。即 \(\forall _{a\in \mathbb{N}} a+1\not=0\)
- 不同的自然数有不同的后继数。即 \(\forall _{a\in \mathbb{N}} a+1\not=a\)
- 自然数集只包括上述四条所述的数。形式化的说,设 \(S\) 是 \(\mathbb{N}\) 的子集,满足上述四条的性质(将自然数替换为 \(S\) 中的元素),则 \(S=\mathbb{N}\)。
记号 \(\forall\)
\(\forall\) 形象是一个倒过来的
\[\forall_{a\le10}a\le5 \]A,取自英文单词 any,表示对于任意一个。例如表示对于每个小于等于 \(10\) 的数 \(a\),都有 \(a\) 小于等于 \(5\)。
\(\forall\) 的 \(\LaTeX\) 代码为
\forall
值得一提的是,我们给每个自然数设计有记号,\(2=1+1,3=2+1,4=3+1,\cdots\)。
加法结合律戴德金-皮亚诺结构
一个戴德金-皮亚诺结构为一满足下列条件的三元组(X, x, f):
- \(X\) 是一集合,\(x\) 为 \(X\) 中一元素,\(f\) 是 \(X\) 到自身的映射;
- \(x\) 不在 \(f\) 的像集内;
- \(f\) 为一单射。
- 若 \(A\) 为 \(X\) 的子集并满足 \(x\) 属于 \(A\),且若 \(a\) 属于 \(A\),则 \(f(a)\) 亦属于 \(A\),则 \(A=X\)。
小学时好像是先学交换律才学结合律的呀?但是交换律的证明需要先证明结合律……
定理1.1 自然数加法满足结合律,即 \(\forall_{a,b,c\in\mathbb{N}}(a+b)+c=a+(b+c)\)
证明:
- 当 \(a=0\) 时,\((0+b)+c=b+c=0+(b+c)\)
- 假如 \(a=k\) 时原定理成立,则对于 \(a=k+1\),有\[\begin{align}a+b+c&=(k+1+b)+c\notag\\ &=((k+b)+1)+c \notag\\ &=((k+b)+c)+1 \notag\\&=(k+(b+c))+1\notag\\&=k+1+(b+c)\notag\\&=a+(b+c)\notag\end{align} \]当 \(x=k+1\) 时原定理成立。
由上述两条可推理出,原定理恒成立。\(\qquad\qquad\blacksquare\)
加法交换律定理1.2 自然数加法满足交换律,即 \(\forall_{a,b\in\mathbb{N}}a+b=b+a\)
在证明之前,我们需要先证明两个引理:
引理1.3 \(\forall_{x\in\mathbb{N}}0+x=x\)
证明:
- 当 \(x=0\) 时,\(0+x=0+0=0\)
- 假如当 \(x=k\) 时原引理成立,则当 \(x=k+1\) 时,\(0+x=0+k+1=(0+k)+1=k+1=x\),即当 \(x=k+1\) 时原引理成立。
由上述两条可推理出,原引理恒成立。\(\qquad\qquad\blacksquare\)
引理1.4 \(\forall_{x\in\mathbb{N}}1+x=x+1\)
证明:
- 当 \(x=0\) 时,\(1+0=1=0+1\)
- 假如当 \(x=k\) 时原引理成立,则当 \(x=k+1\) 时,\(1+k+1=(1+k)+1=(k+1)+1\),即当 \(x=k+1\) 时原引理成立。
由上述两条可推理出,原引理恒成立。\(\qquad\qquad\blacksquare\)
证明定理1.2:
- 当 \(a=0\) 时,\(0+b=b=b+0\)
- 假如当 \(a=k\) 时原引理成立,则当 \(a=k+1\) 时,\(a+b=k+1+b=k+b+1=b+k+1\),即当 \(x=k+1\) 时原引理成立。
由上述两条可推理出,原定理恒成立。\(\qquad\qquad\blacksquare\)
整数通项归纳法
让我们想想多米诺骨牌排成一行,那么我们只要把任意一张排推到,那么在这张牌之后的每一张派都会被因连锁反应而被前一张牌推到。即使在此之后的有无穷张多米诺骨牌,它们也终会全部倒下。这使我们战胜了无限。
这种方法在数学上被称为通项归纳法(mathematical induction),上面的几个证明都使用了这个方法。
让我们再举一个例子,令
\[S_n=0^2+1^2+2^2+3^2+\cdots+n^2 \]求证:
\[S_n=\frac{1}{6}n(n+1)(2n+1) \]证明:
- 第一步:\[S_0 = 0^2 = 0 = \frac{0 (0 + 1) (2\ 0 + 1)}{6} \]即,当 \(n = 0\) 时,等式成立。
- 第二步:我们现在假设当 \(n = k\) 的时候原等式成立。
即现在证明当 \(n = k + 1\) 时成立。具体而言,是这样做的:\[\begin{aligned}S_{k + 1} &= S_k + (k + 1)^2\\&= \frac{k(k + 1)(2k + 1)}{6} + (k^2 + 2k + 1)\\&= \frac{2k^3 + 9k^2 + 13k + 6}{6}\\&= \frac{(k + 1)((k + 1) + 1)(2(k + 1) + 1)}{6}\end{aligned} \]由此得证,若 \(n = k\) 时等式成立,则当 \(n = k + 1\) 时等式成立。
而当 \(n = 0\) 时等式成立,则对于 \(\forall_{n \geq 0}\),原等式成立。\(\qquad\qquad\blacksquare\)这里的“第一张多米诺骨牌”正是"\(n = 0\) 时成立",而第二步的证明中则把“牌”排了起来。于是无限的“牌”全部倒了。通项归纳法可以说是数学证明中的“万金油”。
加法逆元自然数集是不完整的,在群论中被称为“半群”,而整数集则是完整的。
减法来自何方?
进行加法运算时,我们关于数 \(a\) 定义一个数 \(x\),使得
\[a+x=0 \]则称 \(x\) 为 \(a\) 的加法逆元,记作 \(-a\)。由此我们得到
\[a+(-a)=0 \]根据加法单位元的性质,加上一个数的加法逆元,相当于消除了加这个数的影响。
例1.5 已知 \(2+x=6\),求 \(x\)。
解:
\(\because 2\) 的加法单位元为 \(-2\)
\(\therefore x=6+(-2)\)\(\qquad\qquad \texttt{w5}\)
\(\texttt{w5}\) 和 \(\blacksquare\) 记号
\(\texttt{w5}\) 是 which was what we wanted 的缩写,表示回答完毕,解答过程的结束。
\(\blacksquare\) 表示证毕,只用于证明过程的结束。表示证毕的常用记号还有 \(\texttt{Q.E.D}\)。
由此,代数的说,若 \(a+x=b\),则 \(x=b+(-a)\)。
减法减法,只是加上加法逆元的简写。
由于 \(a+(-b)\) 很常用,而且书写称呼都不方便,我们设计一种新的二元运算,称为减法,作为加加法逆元的简称,即
\[a-b=a+(-b) \]负数\(3\) 的加法逆元是多少,是自然数集的元素吗?
整数集(记作 \(\mathbb{Z}\))是自然数集的拓展,引入了负数的概念。简而言之:
- 如果 \(n\) 是自然数,则 \(n\) 是整数。
- 如果 \(n\) 是自然数,则 \(-n\) 是整数。
- 整数集只包括上述满足两条性质的数。
即 \(\forall_{x\in\mathbb{N}}x,-x\in\mathbb{Z}\) 且 \(\forall_{x\in\mathbb{Z}}x\in \mathbb{N} \lor -x\in\mathbb{N}\)。
逻辑记号:\(\lnot\lor\land\)
\(\lnot\) 表示逻辑非,即 \(\lnot a\) 为真当且仅当 \(a\) 为假。
\(\lor\) 表示逻辑或,即 \(a\lor b\) 为真当且仅当 \(a\) 为真或 \(b\) 为真。
\(\lor\) 表示逻辑且,即 \(a\land b\) 为假当且仅当 \(a\) 为假或 \(b\) 为假。
比起自然数集,整数集多了负数(negative number),这使得整数集比自然数集更加完整:整数集中的每个数的加法逆元都能在整数集中找到,而只有 \(0\) 能在自然数集中找到加法逆元。
在整数集上,加法结合律和加法交换律任然成立(读者自证不难)。
有理数乘法逆元在乘法意义下,整数集完整吗?
怎么把 \(7\) 颗糖分给 \(3\) 个小朋友?
进行乘法运算时,我们关于数 \(a\) 定义一个数 \(x\),使得
\[a+x=1 \]则称 \(x\) 为 \(a\) 的乘法逆元(在不产生歧义的前提下可以简称为逆元),暂时记作 \(\frac{1}{a}\)。由此我们得到
\[a\frac{1}{a}=1 \]根据乘法单位元的性质,乘以一个数的乘法逆元,相当于消除乘以这个数的影响。
除法你喜欢 \(a/b\),\(a\div b\),\(a:b\),还是 \(\frac{a}{b}\)?
我喜欢第一个,因为它使用的 \(LaTeX\) 记号最少,写起来最快。
既然减号是加号的一部分,除号也应该是乘号的一部分,不是吗?
由于 \(a\frac{1}{b}\) 很常用,而且书写称呼都不方便,我们设计一种新的二元运算,称为除法,作为乘乘法逆元的简称,即
\[\frac{a}{b}=a\frac{1}{b} \]分数\(3\) 的乘法逆元是多少?它是整数集的元素吗?
有理数集(记作 \(\mathbb{Q}\))是整数集的拓展,对于任意两个整数 \(a,b\),满足\(\frac{a}{b}\) 是有理数。即 \(\mathbb{Q}=\{\frac{a}{b}|a,b\in\mathbb{Z}\}\)。
运算性质在有理数域上,加法结合律和加法交换律任然成立(读者自证不难)。
并且,
定理1.6 有理数乘法满足结合律。即 \(\forall_{a,b,c\in\mathbb{Q}}(ab)c=a(bc)\)
定理1.7 有理数乘法满足交换律。即 \(\forall_{a,b\in\mathbb{Q}}ab=ba\)
定理1.8 有理数加法和乘法满足分配律。即 \(\forall_{a,b,c\in\mathbb{Q}}a(b+c)=ab+ac\)
以上三条定理读者自证(好像有点难?),或视为加法和乘法定义的一部分即可。
根据分配率,我们注意到负数乘以负数得到一个正数。
数轴数有怎样的几何直观体现?
画一条直线,在直线上选两个点,分别为 \(0\) 和 \(1\),并根据 \(0,1\)之间的位置关系标记出正方向,这就叫做数轴(number axis)。
真·通俗版定义
下面是一个数轴的例子:

加法有怎样的几何(数轴)直观体现?
加法就是横向平移数轴,例如 \(+3\) 就是将数轴左移 \(3\) 个单位。
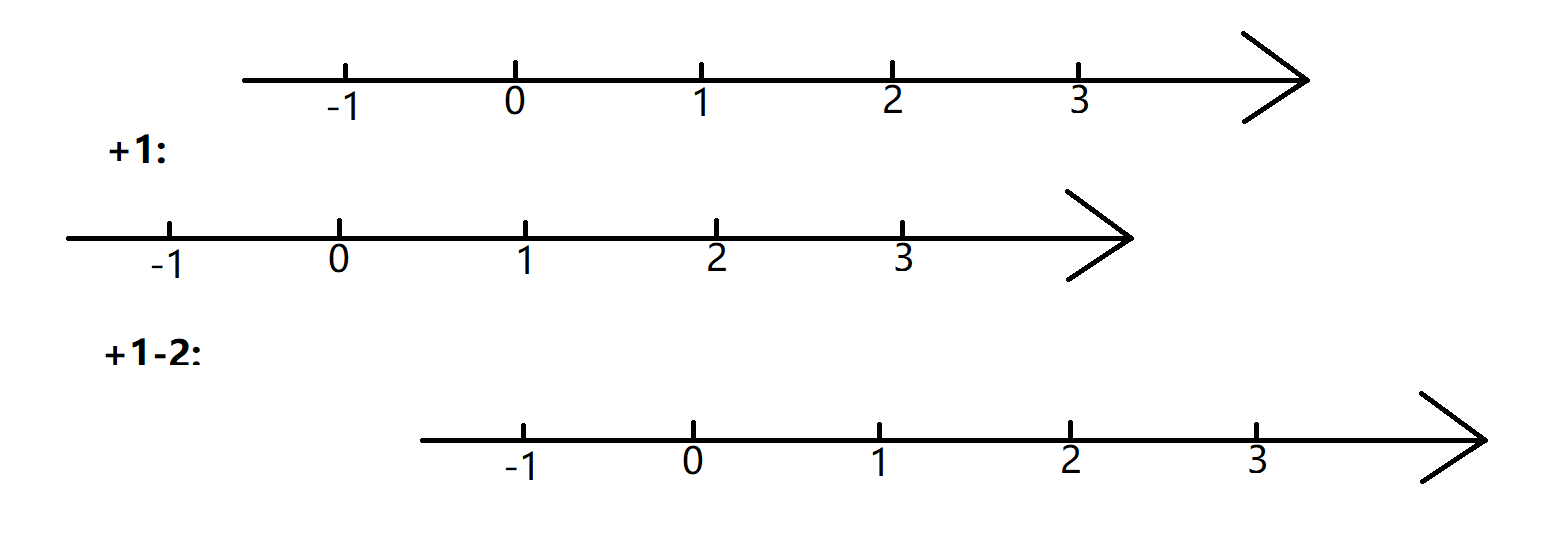
画图画的?有点没对齐!
乘法变换乘法有怎样的几何(数轴)直观体现?
乘法就是缩放数轴,例如 \(\times 3\) 就是将数轴缩小 \(3\) 倍。
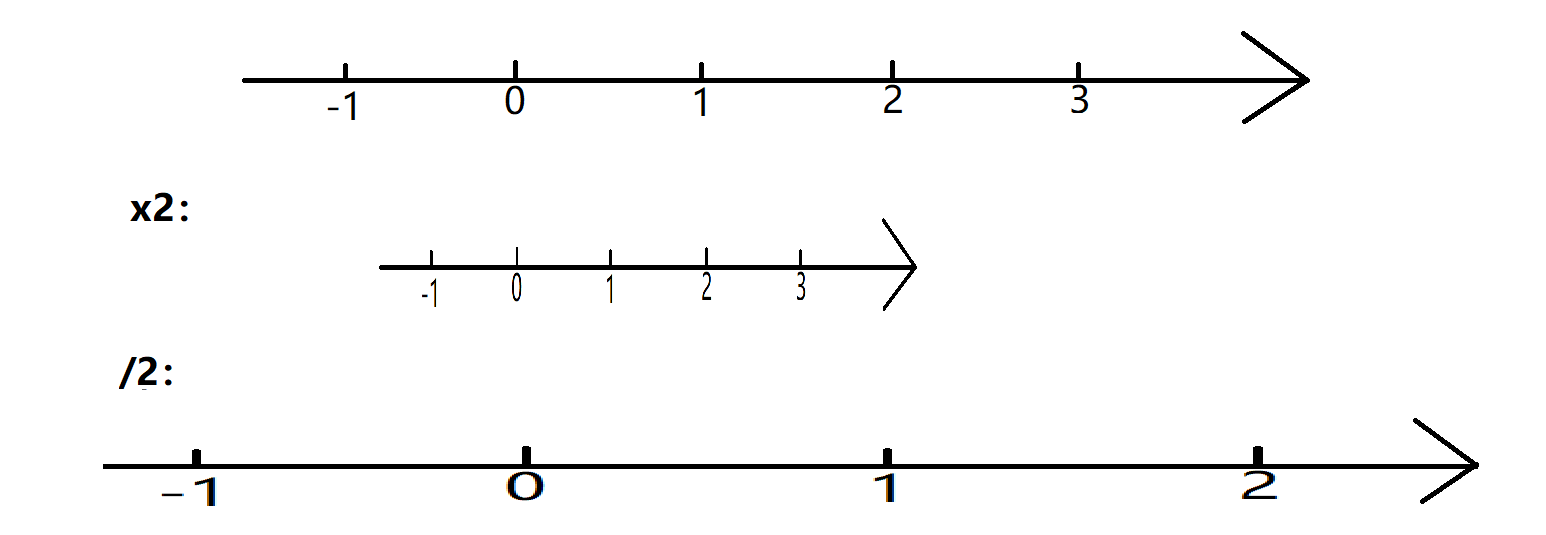
根据分配率,乘负数就是缩放并翻转数轴方向。
乘方连加得乘,连乘得……
求 \(n\) 个 \(a\) 乘积的运算,叫做乘方(power),记作 \(a^n\)。特别的,定义 \(a^0=1\)。例如,\(3^4=81\)。
容易注意到,乘方并没有交换律(\(3^4=81,4^3=64\))。但是乘方拥有几条重要性质(不妨称为乘方的基本性质):
- \(\forall_{a,n,m}a^na^m=a^{n+m}\)
- \(\forall_{a,n,m}\frac{a^n}{a^m}=a^{n-m}\)
- \(\forall_{a,n,m}(a^n)^m=a^{nm}\)
上一节的定义并不完整(要求 \(n\) 为自然数),我们拓展这个定义。使得新定义满足两条乘方的基本性质。
例如我们要计算 \(4^{\frac{3}{2}}\),由性质 1 得到
\[4^{\frac{3}{2}}=4^14^{\frac{1}{2}}=4\ 4^{\frac{1}{2}} \]那么 \(4^{\frac{1}{2}}\) 等于多少呢?不妨设 \(x=4^\frac{1}{2}\),由性质 3 知道,
\[x^2=(4^\frac{1}{2})^2=4 \]所以我们是想要知道,什么数 \(x\) 满足 \(x^2=4\),容易注意到 \(2\) 和 \(-2\) 都符合条件。我们定义当有两个数满足条件时,计算平方总是使用较大的那一个,即
\[4^\frac{1}{2}=2 \]所以 \(4^{\frac{3}{2}}=4\ 4^{\frac{1}{2}}=4\ 2=8\)
关于负数的乘方则可以这样运算:
\[\begin{align}a^{-b}&=a^{0-b}\notag\\&=\frac{a^0}{a^b}\notag\\&=\frac{1}{a^b}\notag\end{align} \]由此之后,我们把 \(a\) 的乘法逆元记为 \(a^{-1}\),这样的记号清晰且节省空间。
算术开根\(a^{\frac{1}{2}}=?\)
由于 \(a^\frac{1}{b}\) 很常用,而且书写称呼都不方便,我们设计一种新的运算,称为算术开根,作为乘方乘法逆元的简称,即
\[^b\sqrt{a}=a^\frac{1}{b} \]算术开根 \(^b\sqrt{a}\)的意义就是求一个数 \(x\) 满足 \(x^b=a\)。当 \(b=2\) 时,可以省略 \(b\),即 \(\sqrt{a}=^2\sqrt{a}\)。特别的,此时的运算叫做算术平方根(squre root)。
对数运算\(10000\) 乘 \(10000000\) 等于多少?你会列竖式计算吗?
不,前者有 \(4\) 个 \(0\),后者有 \(7\) 个 \(0\),所以结果有 \(4+7=12\) 个 \(0\),即 \(1000000000000\)。
为什么能这样计算?
对数运算是乘方运算的一种逆运算,具体而言就是求解一个数 \(x\) 满足
\[a^x=b \]记
\[x=\log_ab \]其中 \(\log\) 就是对数记号。
- 当 \(a=2\) 时,\(a\) 可以省略,即 \(\log b=\log_2 b\)。
- 我们称 \(a=10\) 的对数叫做常用对数(common logarithm),并记为 \(\lg b\)
对数拥有一些基本的性质:
定理1.9 \(\forall_{a,b,c}\log_abc=\log_ab+\log_ac\)。
证明:
\(a^{\log_abc}=bc=a^{\log_ab}a^{\log_ac} \qquad\qquad\blacksquare\)
推论1.10 \(\forall_{a,b,c}\log_ab^n=n\log_ab\)。(读者自证不难)
推论1.11 \(\forall_{a,b,c}\log_{a^n}b=\frac{1}{n}\log_ab\)。(读者自证不难)
定理1.12 (换底公式)\(\forall_{a,b,c}\log_ab=\frac{\log_cb}{\log_ca}\)。
证明:
令 \(x=\log_ab\),则 \(a^x=b\),注意到
\[c^{x\log_ca}=(c^{\log_ca})^x=a^x=b \]两边取对数得
\[x\log_ca=\log_cb \]代入 \(x\) 并移项得
\[\log_ab\log_ab=\log_cb \]即 \(\log_ab=\frac{\log_cb}{\log_ca} \qquad\qquad\blacksquare\)
无理数问题还是出在乘法上……
什么数乘以它自己等于 \(2\)?或者说,\(\sqrt{2}=?\),答案是有理数集的元素吗?
我们知道,有理数总是有限小数或无限循环小数。
无理数(irrational number)则是无限不循环小数,一般包括代数数(algebraic number)和超越数(transcendental number),我们将在之后(第四章)继续讨论这两种数的区别。
连分式我们注意到,一些乘方算式的结果,不总是有理数,或者说,不总能用一个分数表示。
考虑把任意有理数写成连续的分数嵌套形式,使得分子始终是 \(1\)。例如
\[\frac{7}{5}=1+\frac{1}{2+\frac{1}{2}} \]\[\frac{19}{8}=2+\frac{1}{2+\frac{1}{1+\frac{1}{2}}} \]称为连分式。
任何有理数都可以写成有限项的连分式,但是无理数不能,例如
\[\sqrt{2}=1+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{\ddots}}}} \]实数作为一个总称,它完整了吗?
有理数和无理数,总称为实数(real number)(记作 \(\mathbb{R}\))。
实数运算律上文提及的加法结合律、加法交换律、乘法结合律、乘法交换律、加法乘法分配率、乘方基本性质、对数基本性质在实数集上均成立。
实数集的完整性封闭性:
实数集对加、减、乘、除(除数不为零)四则运算具有封闭性,即任意两个实数的和、差、积、商(除数不为零)仍然是实数。
有序性:
实数集是有序的,即任意两个实数 \(a,b\) 必定满足并且只满足下列三个关系之一: \(a<b,a=n,a>b\)。(我们将在以后详细讨论数学关系)
阿基米德性质:实数具有阿基米德性质(Archimedean property),即 \(\forall_{a,b\in\mathbb{R},a>0}\exists_{n\in\mathbb{N}}an>b\)
记号 \(\exists\)
\(\exists\) 形象是一个倒过来的
\[\exists_{a\le10}a>0 \]E,取自英文单词 exists,表示至少存在一个。例如表示至少存在一个小于等于 \(10\) 的数 \(a\),满足 \(a\) 大于 \(0\)。
稠密性:实数集具有稠密性,即两个不相等的实数之间必有另一个实数,既可以是有理数,也可以是无理数。
习题- 在课本上,加法逆元和乘法逆元的名称叫什么?
- \(0\) 可以有乘法逆元吗?有人认为可以定义 \(0\) 的乘法逆元为 \(\infty\),即定义 \(\frac{1}{0}=\infty\),这样可行吗?
- 整数集比自然数集大吗?有理数集比整数集大吗?实数集比有理数集大吗?
- 如何使 \(0^0\) 有意义?
- 在所有无理数中,最无理的数(the most irrational number)是什么?(你需要自己定义什么叫更无理)
- 实数集完整了吗?
- 一个实数总可以被表示成根式(嵌套)的形式吗?
- 一个实数总可以被表示成一个系数都是整数的多项式的根的形式吗?
