手把手建立Roofline模型（CPU）

Roofline模型原理

Roofline模型是由加州理工大学伯利克提出的用来建立当前计算平台在不同的计算强度（Operational Intensity）下能够达到的理论计算上限 。论文和基础理论和应用 Roofline Model与深度学习模型的性能分析 。本文旨在教授如何根据当前开发环境机器建立该模型，并简单的介绍如何根据算法计算OI(计算强度)。

需要准备的硬件参数

对于CPU而言，我们需要一下参数：

频率 内存带宽(double) Avx512 Unit Fma Intel® Xeon® Gold 6148 2.7GHz 39.74GB/s 2 2

其中Avx512、Fma并非是必备参数。

查询CPU相关指标方法或网站:

• <https://ark.intel.com/content/www/us/en/ark/products/120489/intel-xeon-gold-6148-processor-27-5m-cache-2-40-ghz.html>
• <https://en.wikichip.org/wiki/intel/xeon_gold/6148>
• 在LINUX 下可以使用lscpu 查询.

计算相关参数：
当前CPU的理论峰值：

\[理论性能峰值 ={频率*512*AVX数量*FMA \over 32/64} \]

AVX和FMA并不是必要参数，32/64取决于当前处理问题是单精度（32）或者双精度（64）

由上述公式，我们可以计算出Xeon Gold 6148的计算双精度理论性能峰值为2.7GHz*2(avx)*2(FMA)/64=86.4Gfplos。

计算当前内存带宽：

通常情况下我们可以通过 wikichip 搜索到，当然也可以通过 StreamBenchmark 程序获取。

建立Roofline模型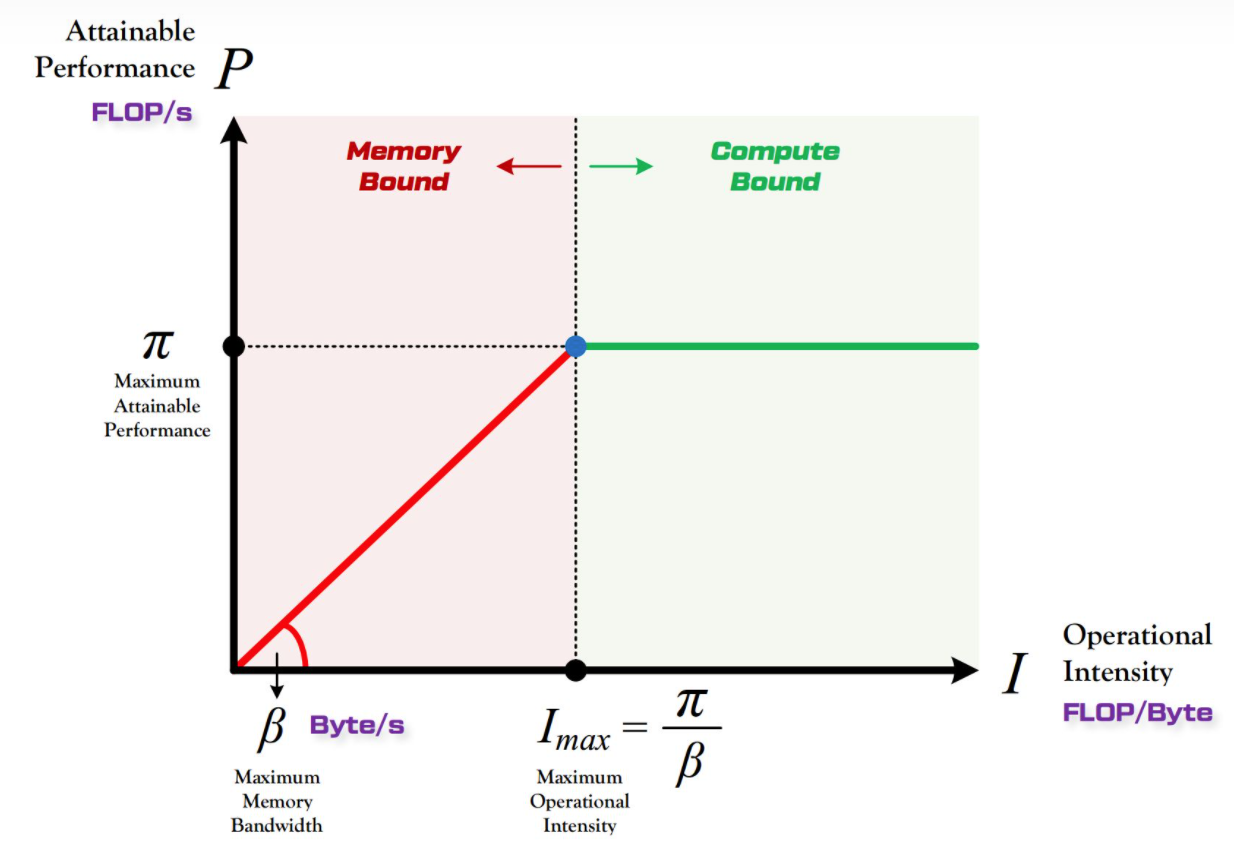

Roofline模型中的相关参数公式如下，并计算Xeon Gold 6148 的参数：

• \(\pi=理论性能峰值\) ，根据上文内容，我们已经计算出当前CPU的理论性能峰值就是86.4Gflops。
• \(\beta=理论内存带宽\) ，上一章节有关于理论内存带宽获取方式，当前CPU的值为39.74Gflops。
• \(I_{max} = {\pi \over \beta}\) ，显然易得当前值为2.17。

根据当前算法计算OI 访存密集型算法

void saxpy(double *a,double * b,double* c,int n,int s)
{
    for(int i=0;i<n;++i){
        a[i]=b[i]*s+c[i];
    }
}

分析程序的AI

该程序循环内做了一次乘法和一次加法，读取了三个数据，已知操作的数据都为64位浮点数，那么 \(OI={2*N \over 8*3*N}={1 \over 12}\)。根据公式 \(FLOPS=OI \times BW(bound witdh)\) 可得当前的算法的理论峰值为~3.3Gflops。实际测试结果为2.4Gflops，存在可能优化的空间。

运算密集型算法

最简单的运算密集型程序为矩阵乘法 。这里就不具体算法实现展示。直接分析程序的OI，假设矩阵的的大小为 \(M\) ，矩阵乘需要加载两次矩阵，并写入一次矩阵，那么总的数据加载读取量为 \(3 \times M \times M\) ，矩阵乘的每个元素需要需要进行 \(M\) 次乘操作和 \(M-1\) 次加操作，因此，计算总量为 \(2*(M-1) \times M^2\) ，当不考虑数据是64位浮点时，可得 \(OI={2*(M-1) \over 3*8}\) 。当矩阵大小大于40时，对于当前CPU输入计算密集型程序，可达到的理论峰值为86.4Gflops。

优化方式

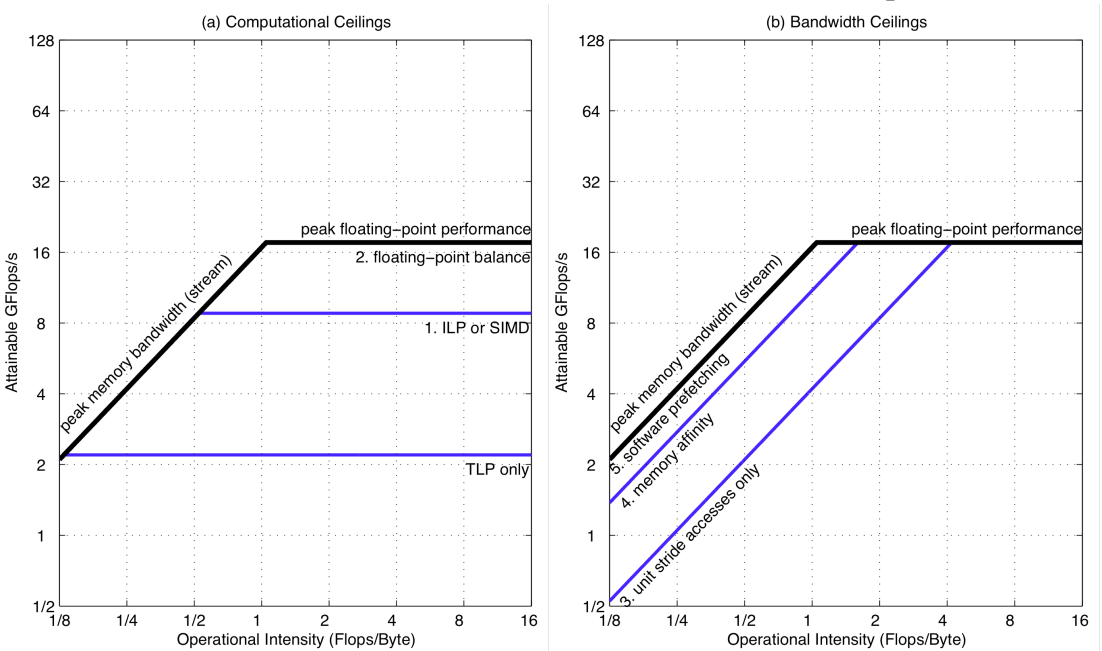
论文 给出了一些可以优化的方式：

• 针对访存密集型程序，可以通过soft perfetch等技术优化。
• 针对计算密集型程序，可以通过SIMD等技术优化。