分子动力学模拟算法框架

分子动力学模拟是一个跨越众多学科领域的强大工具，从物理学的角度来看分子动力学模拟的话，其基于量子力学（量子化学）构建模型，通过牛顿力学进行演化迭代，最后能够在时间平均上等同于统计力学的系综平均，是一个堪比复变函数欧拉公式的优美过程。本文就当前分子动力学模拟的框架进行了整体介绍，其中并不展开讲解各项技术内容，但是也为感兴趣的研究人员提供一个简单的入口。 技术背景

分子动力学模拟在新材料和医药行业有非常重要的应用，这得益于分子动力学模拟本身的直观表述，用宏观的牛顿力学，结合部分微观的量子力学效应，就能够得到很好的符合统计力学推断的结果。可以说，分子动力学模拟从理论上跨越了物理化学生物等多个学科，而从实践上又包含了计算机科学、人工智能的大量辅助和优化，综合性非常强。越是综合性强的研究方向，就越有必要梳理清楚其主干脉络和工作流程。

1 坐标和速度的初始化

当我们需要研究一个特定的体系时，首先需要指定这个体系的初始空间和坐标，再进行演化。初始坐标的获取方式有很多种，比如从数据库中直接获取、根据拓扑结构用特定的工具进行生成（比如之前的博客介绍过的OpenBabel），还有就是在材料学领域常用的根据晶体结构去生成有规律的体系初始坐标。初始速度的选取方式，其实可以选择全0的初始状态，让体系在力场作用下进行自由演化；也可以给全随机的初始速度，让一开始的体系能量和温度达到一个比较高的值，有可能可以提高模拟的效率；还有一种在材料学领域比较常用的方法，就是指定一个初始温度，通过能均分定理对体系中的各个原子进行速度分配。如下所示是一个通过OpenBabel生成一个水分子初始坐标的简单示例：

$ obabel -:O --gen3d -omol2 -O H2O.mol2
1 molecule converted
$ cat H2O.mol2
@<TRIPOS>MOLECULE
*****
 3 2 0 0 0
SMALL
GASTEIGER

@<TRIPOS>ATOM
      1 O           0.9606    0.0592    0.0649 O.3     1  HOH1       -0.4105
      2 H           1.9285    0.0383    0.1064 H       0  HOH0        0.2052
      3 H           0.6818   -0.3573    0.8942 H       0  HOH0        0.2052
@<TRIPOS>BOND
     1     1     2    1
     2     1     3    1

应该说，在坐标的初始化中，由于分子本身的性质很大程度上是由其拓扑连接性所决定的，所以生成分子初始坐标要以拓扑结构为依据。而初始速度的选取，更多的是一种经验方法，只要初始速度值不要过大（否则会使体系剧烈震荡甚至奔溃），怎么选取初始速度就只是影响最终的模拟效率。比较典型的一个案例就是通过Shooting的方法对化学反应过程进行加速，其实也是对初始速度的一个调整。

2 Neighbor List与Cell List

在计算非键相互作用时，如果对一个\(N\)原子的体系进行遍历，可达\(\frac{N(N-1)}{2}\)的计算量。由于模拟的体系一般都较大，\(O(N^2)\)的复杂度属实有点高了。因此为了简化计算量，一方面通过球形截断来选取近邻表（如下图所示，图片来自于参考链接1）：

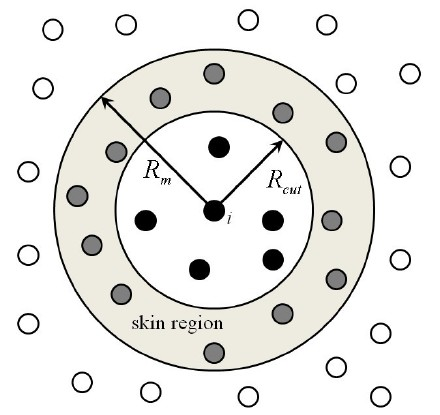
仅在截断的球形范围内考虑两两相互作用。再对空间进行切割，构建Cell List，只要设定好Cell List的大小，比如设定正方体Cell List的边长等于截断半径，这样一来，我们在统计一个Cell中的近邻关系时，只需要关注总共周边的27个Cell中的原子即可，大大缩减了计算量。Cell List示意图如下所示（图片来自于参考链接2）：

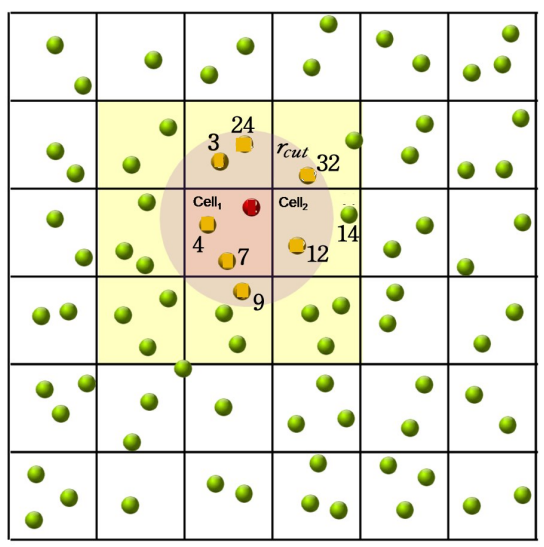
关于Cell List的实现，此前笔者专门写过一篇博客用于介绍在Python中的GPU加速打格点算法实现，大致效果如下：

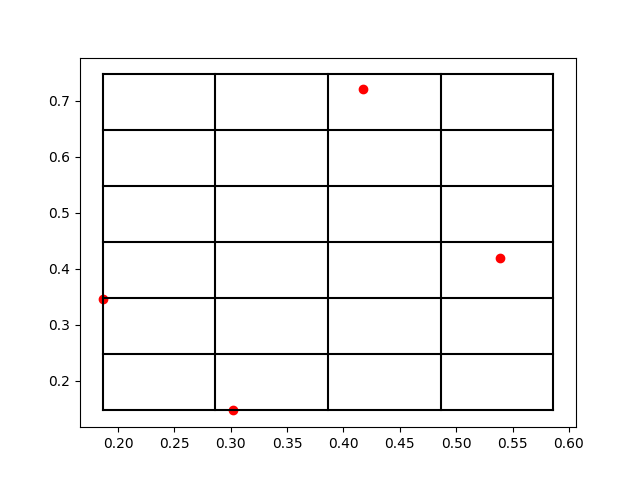
由于是用了GPU来计算，因此有较好的性能表现。一般情况下，构建近邻表的这一步是对GPU的显存要求最高的步骤之一。即使是使用了Cell List的方法，一般也不会每一步都去更新近邻表。常用的策略是，设置一个interval，比如5-10，也就是每5-10步更新一次近邻表。而且也不需要再去检索整个邻近的Cell中的所有原子，只需要监测skin region中的原子变动即可。这也是设立一个缓冲区skin region的原因，当然，我们需要保障在指定的interval下原子不会跑的太远。

3 获取作用力

获取作用在每一个原子或者团簇上的作用力的方法有很多种，比如量子化学的ab-initio的方法、拟合力场的方法以及近几年发展出来的深度学习的方法，都有非常多的应用且各有优势。从头算的量子化学方法，精度非常高，但是耗时较长。拟合力场速度非常快，精度也在可接受的范围内，是传统分子动力学模拟中应用最广泛的方法。但是这两个方法都要面临一个问题：需要手动微分，要么就是复杂的解析推导，要么就是数值差分。而现在计算机领域的各种深度学习框架，都已经提出了最新的解决方案：自动微分。因此，使用深度学习的方案去构建力场，在充分的训练集和合理的损失函数下，可以达到非常快的速度以及可以接受的精度。还有两个非常重要的点：整个过程只要使用深度学习的算子，就是完全连续可微的，而且往往这些深度学习框架都对硬件系统有非常好的可拓展性和可迁移性。

除了上述的三种方法之外，结合这几年非常火的量子计算，又出现了新的基于量子计算机的分子动力学模拟框架，比如参考链接3和参考链接4。目前来说已经提出来的主要框架还是基于Variational Quantum Eigensolver变分量子求解器（VQE），通过VQE可以计算出来类似于量子化学从头算方法的势能面，进而根据费曼-赫尔曼定理做差分得到原子上的作用力，就可以用于分子动力学的模拟了。由于这里细节较多，在本文不进行展开讲解，需要后面专门开一篇文章介绍VQE的框架。简单点评一下这两个基于VQE的分子动力学模拟的工作的话，就是只适用于当下量子芯片的Demo使用，距离真在在分子动力学模拟场景下的应用还非常的遥远。而VQE框架本身是NISQ近期量子计算时期下所诞生的产物，其最promising的点在于，可以在近期含噪的量子芯片下实现一个比较大规模体系的分子的势能面的计算（计算量已经超越了传统计算机的范畴），但是实际操作中在精度和速度上是否能有优势，暂时还是存疑的状态。另外，基于类似的变分量子计算的框架，还出现了量子机器学习这个两大buff加持的算法框架，同样可以参考传统深度学习的方法实现一个量子计算版本的神经网络来替代力场，目前似乎还没人这么做。

4 积分器/体系演化

在具备了初始状态的坐标和速度，以及上一步计算得到的原子作用力之后，就可以使用牛顿力学让体系向前演化一步。其中涉及到的算法内容，可以参考上一篇博客从刘维尔方程到Velocity-Verlet算法，其中主要就是Verlet、LeapFrog和Velocity-Verlet三个算法，在分子动力学模拟中也叫积分器。这个部分的计算量并不是很大，但是会导致体系的运动，如果需要保存中间过程，注意每隔一定的模拟步数，要把轨迹保存下来。

5 判断控制/约束条件

上一个章节中说的是体系的运动，那么在一定的时间步长（通常是一个飞秒）下，原子运动的幅度大小，是跟多个因素相关的：1. 原子本身收到的作用力大小；2. 原子的质量；3. 在控温控压，有可能受到系统粘滞作用力的影响或者碰撞影响，也有可能被缩放；4. 对于加了约束条件的过程，还会受到施加的约束作用，比如等效的键向作用力（施加约束的过程，本身就是为了控制部分原子之间相对位置大小）。因此，我们在分子动力学模拟的演化过程中，还需要考虑这些控制和约束的方法。

常用的控温技术有：Andersen Thermostat速度重置方法、Berendson Thermostat速度缩放方法和Extended Ensemble扩展系综方法。但是Andersen Thermostat存在相空间轨迹不连续的问题，Berendson Thermostat可能会导致不合理的相的出现，因此最常用的就是几种扩展系综的方法：Nose-Hoover Thermostat、Nose-Hoover Chain Thermostat和Langevin Dynamics Thermostat，这些方法的基本原理就是在系统哈密顿量上加上温度的相关项，这样就可以驱动系统演化到一个温度恒定的本征态上，以达到控温的目的。常用的控压技术有：Volume Rescaling体积重设方法、Berendsen Barostat体积坐标缩放方法和Extended Ensemble。类似于控温技术的，最常用的还是在哈密顿量上加一个体积项，通过驱动系统演化到一个稳定体积所对应的本征态，从而达到控制体积的目的。而这里提到的约束条件，相对的就更加具体，常见的比如LINCS算法、SETTLE算法、RATTLE算法和SHAKE等，其基本思想就是固定某两个原子之间的距离保持不变。用一种比较形象的说法就是，在两个原子之间加了一根没有质量的柱子限制两者的相对运动。如下所示是SETTLE算法的实现，先不加约束的位移一步，然后再把约束加进去，同时对坐标和速度进行更新：

6 结果输出与增强采样

经过上面的步骤，我们其实已经完成了一步的分子动力学模拟，如果此时达到了结果输出的点，应该将坐标轨迹保存到一个文件中。需要特别说明的是，有一些格式并不支持持续的数据写入，比如npz格式，每写入一次，就会自动把前面写入的内容全都覆盖，因此要挑选好存储格式，常用的是二进制格式的文件或者文本格式的文件。除了存储完整的坐标轨迹之外，还需要存储一些必要的参数，比如单步的速度等，这样即使程序终止，下一次启动程序的时候也可以从断点开始，而不需要重新开始。

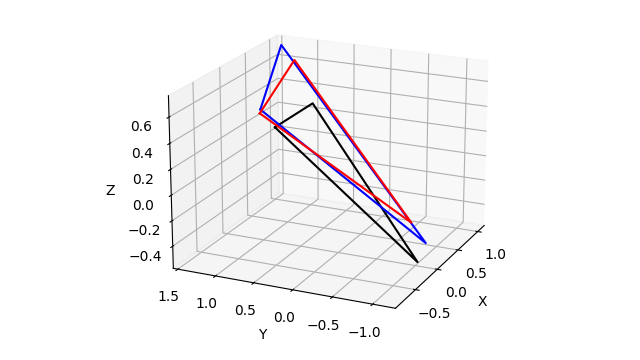
而增强采样（Enhanced Sampling）也是一个基于结果来分析的工作，称之为后处理。虽然是后处理，但是这个处理的结果会反馈到下一步的迭代中去，作为一个独立的等效势能去推动原子的运动。常见的工具是PLUMED，前面写过一篇相关的安装与使用的文章。当然其实采样算法也并不是难以实现，更大的难点是在于跟已有框架的结合与交互，相对来说门槛要高一些。常用的增强采样的方法比如MetaDynamics，可以用这样一个比较具象的案例来描述：在一个自定义的序参量所对应的势能面上堆土，直到分子体系可以在给定的本征态之间快速切换（势能差距较低）。大致结果如下图所示（图片来自于参考链接5）：

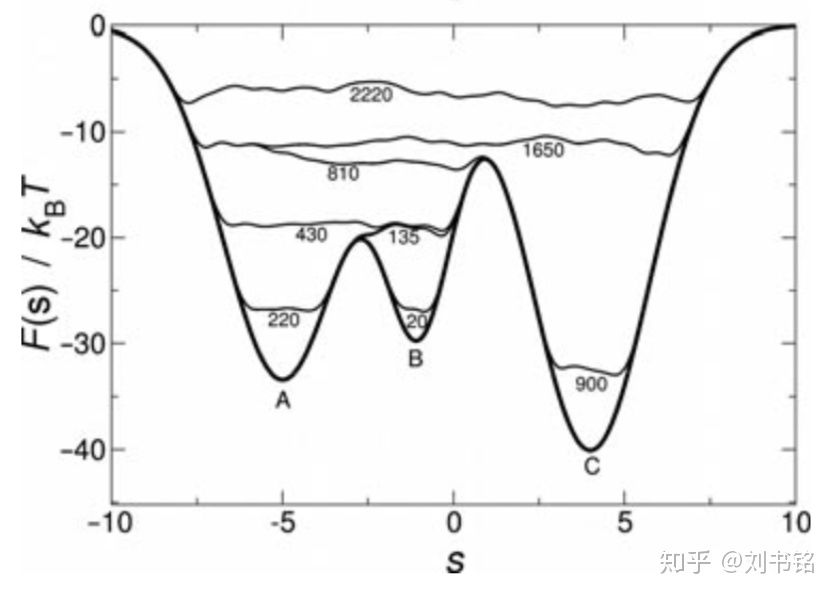
在通过新的坐标更新了力场参数之后，加上增强采样所对应的等效势能产生的等效作用力，就可以开始下一轮的迭代，就重新回到了第3步，不断的迭代，直到达到目标的迭代步数。一般情况下分子动力学没有特别明显的停止迭代的指标，更多的是设定一个时间阈值，达到阈值就停止迭代更新。

总结概要

分子动力学模拟是一个跨越众多学科领域的强大工具，从物理学的角度来看分子动力学模拟的话，其基于量子力学（量子化学）构建模型，通过牛顿力学进行演化迭代，最后能够在时间平均上等同于统计力学的系综平均，是一个堪比复变函数欧拉公式的优美过程。本文就当前分子动力学模拟的框架进行了整体介绍，其中并不展开讲解各项技术内容，但是也为感兴趣的研究人员提供一个简单的入口。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/md-framework.html

作者ID：DechinPhy

更多原著文章请参考：https://www.cnblogs.com/dechinphy/

打赏专用链接：https://www.cnblogs.com/dechinphy/gallery/image/379634.html

腾讯云专栏同步：https://cloud.tencent.com/developer/column/91958

参考链接

1. http://blog.sina.com.cn/s/blog_78f0b32101011mlj.html#:~:text=近邻列表：近邻列表 (neighbor,list，也叫做Verlet list)是分子动力学模拟中为了加速体系粒子间相互作用的力的计算而设置的一种数据结构。
2. https://www.jsjkx.com/CN/article/openArticlePDF.jsp?id=512
3. https://aip.scitation.org/doi/10.1063/5.0046930
4. https://pubs.acs.org/action/showCitFormats?doi=10.1021/acs.accounts.1c00514&ref=pdf
5. https://zhuanlan.zhihu.com/p/95824483

“留一手”加剧内卷，“讲不清”浪费时间。