联邦学习：多任务思想与聚类联邦学习

在联邦学习领域，许多传统机器学习已经讨论过的问题（甚至一些90年代和00年代的论文）都可以被再次被发明一次。比如我们会发现聚类联邦学习和多任务学习之间就有千丝万缕的联系。聚类联邦学习基本上都基于这样一个假设：虽然联邦学习中各节点的数据是Non-IID的，但是我们可以假定某些节点的数据可以归为一个聚类簇（簇内节点的分布近似IID）。实际上，这个思想让我们联想到高斯混合分布。高斯混合分布就假设每个节点的数据采样自高斯混合分布中的一个成分(对应一个簇)，而经典的高斯混合聚类就是要确定每个节点和簇的对应关系。 1.导引

计算机科学一大定律：许多看似过时的东西可能过一段时间又会以新的形式再次回归。

在联邦学习领域，许多传统机器学习已经讨论过的问题（甚至一些90年代和00年代的论文）都可以被再次被发明一次。比如我们会发现聚类联邦学习和多任务学习之间就有千丝万缕的联系。

2. 多任务学习回顾

我们在博客《基于正则化的多任务学习》中介绍了标准多任务学习的核心是多任务个性化权重+知识共享^[1]。如多任务学习最开始提出的模型即为一个共享表示的神经网络：

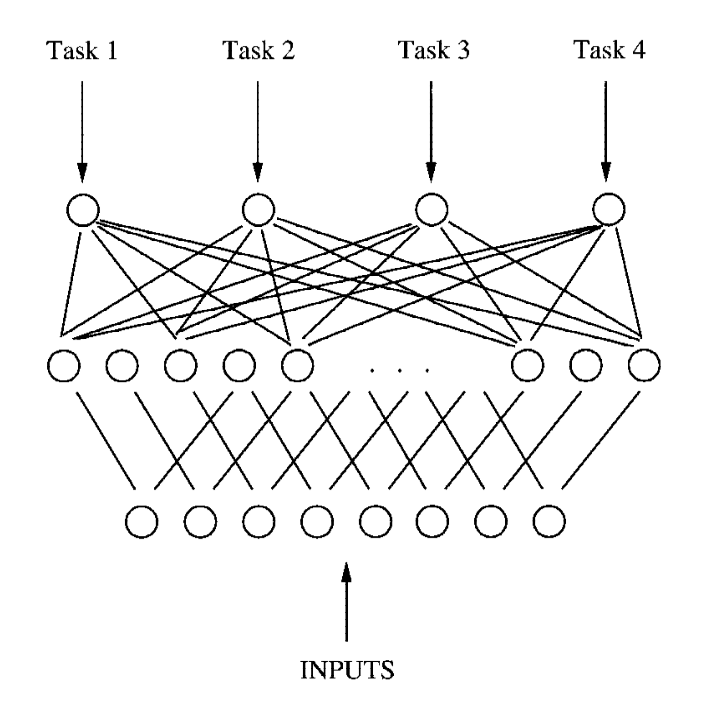
而多任务学习中有一种方法叫聚类多任务学习。聚类多任务学习基本思想为：将任务分为若个个簇，每个簇内部的任务在模型参数上更相似。 最早的聚类多任务学习的论文^[2]为一种一次性聚类(one-shot clustering)，即将任务聚类和参数学习分为了两个阶段：第一阶段，根据在各任务单独学习得到的模型来聚类，确定不同的类簇。第二阶段，聚合同一个类簇中的所有训练数据，以学习这些任务的模型。这种方法把任务聚类和模型参数学习分为了两个阶段，可能得不到最优解，因此后续工作都采用了迭代式聚类(iterative clustering)，即在训练迭代中同时学习任务聚类和模型参数的方法，

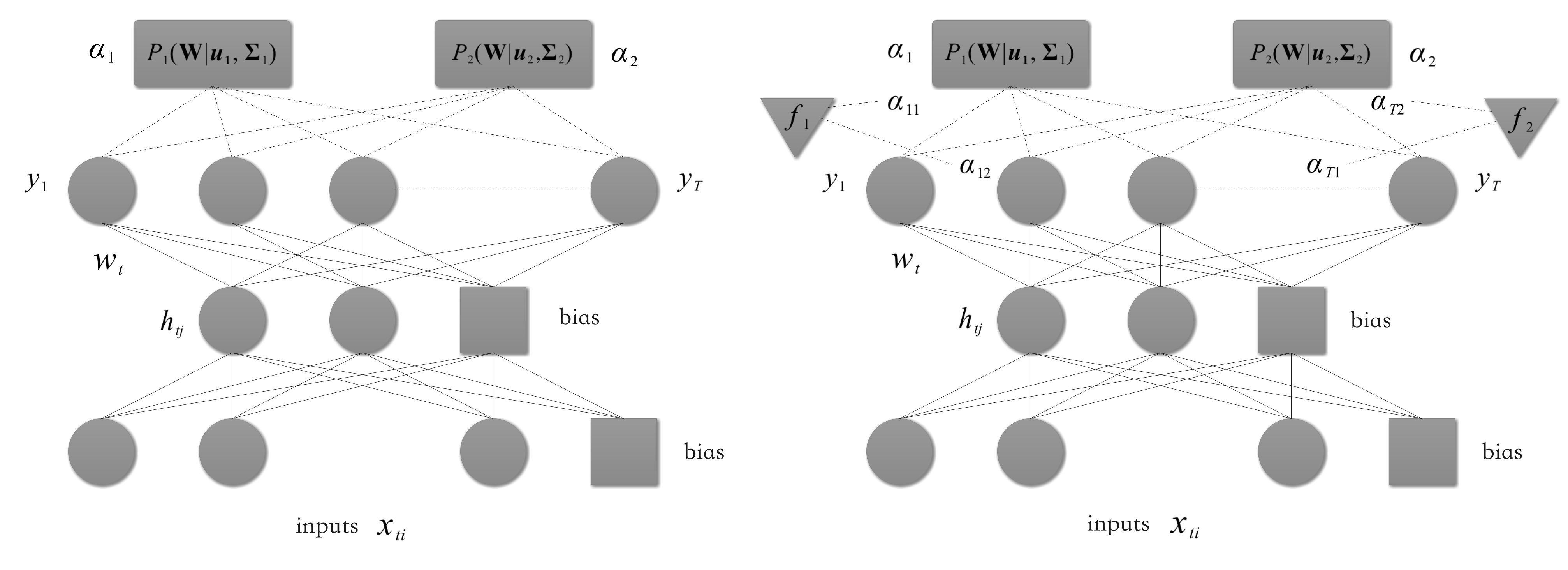
我们着重介绍Bakker等人(2003)^[3]提出了一个多任务贝叶斯神经网络(multi-task Bayesian neural network)，其结构与我们前面所展现的共享表示的神经网络相同，其亮点在于基于连接隐藏层和输出层的权重采用高斯混合模型（Gaussian mixture model）对任务进行分组。若给定数据集\(\mathcal{D} = \{D_t\}, t=1,...,T\)，设隐藏层维度为\(h\)，输出层维度为\(T\)，\(\mathbf{W}\in \mathbb{R}^{T\times (h + 1)}\)代表隐藏层到输出层的权重矩阵(结合了偏置)。我们假定每个任务对应的权重向量\(\mathbf{w}_t\)(\(\mathbf{W}\)的第\(t\)列)关于给定超参数独立同分布，我们假定第\(t\)个任务先验分布如下：

\[\bm{w}_t \sim \mathcal{N}(\bm{w}_t | \bm{u}, \mathbf{\Sigma}) \tag{1} \]

这是一个高斯分布，均值为\(\bm{u} \in \mathbb{R}^{h + 1}\)，协方差矩阵\(\mathbf{\Sigma} \in \mathbb{R}^{ (h+1) \times (h+1)}\)。
我们上面的定义其实假定了所有任务属于一个簇，接下来我们假定我们有不同的簇（每个簇由相似的任务组成）。我们设有\(C\)个簇（cluster），则任务\(t\)的权重\(w_t\)为\(C\)个高斯分布的混合分布：

\[\bm{w}_t \sim \sum_{c=1}^C \alpha_c \mathcal{N} (\bm{w}_t | \bm{u}_c, \mathbf{\Sigma}_c) \tag{2} \]

其中，每个高斯分布可以被认为是描述一个类簇。式\((9)\)中的\(\alpha_c\)代表了任务\(t\)被分为簇\(c\)的先验概率,其中task clustering(如下面左图所示)模型中所有任务对簇\(c\)的加权\(\alpha_c\)都相同；而task-depenent模型（如下面右图所示）中各任务对簇\(c\)的加权\(\alpha_{tc}\)不同，且依赖于各任务特定的向量\(\bm{f}_t\)。

3. 潜在聚类结构的的前置假设

上面我们提到的这种来自于上个世纪90年代的多任务学习思想并未过时，近年来在个性化联邦学习中又重新焕发了生机。这篇文章我们就来归纳一下与多任务学习思想关系密切的联邦学习个性化方法之一——聚类联邦学习。

这类算法采取了一个重要的假设，就是各个client之间的数据存在潜在的簇关系。在实验中进行数据拆分时（我们只考虑图片数据集），我们会先将数据按照常规Non-IID算法划分到client，然后对client中的图片进行旋转处理^[8]。具体的，对于8个client，如果我们设定两个簇，那么对其中4个client中的全部图片（包括训练集/验证集/测试集）都进行旋转180°；如果设定四个簇，则我们对其中的client-1、client2中图片不动，client3、client4中图片旋转90°，client5、client6数据旋转180°，client7、client8数据旋转270°。

这种划分方式，将直接导致非聚类算法（如FedAvg）精度大大降低，因为不同旋转模式之间的client协作起来反而是有害的。此时需要使用我们下面即将介绍的聚类联邦学习算法。聚类联邦学习算法将同一个旋转模式的client聚为一个类簇，簇内节点可以相互进行知识共享，不同簇之间的client之间不能进行知识共享。从而达到了即让节点之间进行知识共享，又减少了不同旋转模式之间的client相互“负影响”的目的。

（其实，很多论文这样创造聚类结构，并以此宣称自己的聚类算法优于非聚类算法如FedAvg，就好比医生故意把病人的腿打断了然后给他治病一样，也算是属于刻意去创造条件了，但或许科研就是这样吧）

注意，虽然这里假定每个聚类簇对应一个旋转模式，但其实不同旋转模式之间的数据仍然可能会有关联。而这就为我们进行簇间的多任务知识共享提供了动机。

按照其聚类的时间，我们按照上文聚类多任务学习的分发，可将聚类联邦学习的方法也分为一次性聚类和迭代式聚类。

一次性聚类即在模型训练开始之前就先对client数据进行聚类。因为client数据不出库，常常将\(T\)个client初步训练后的参数或得到的稀疏数据表征发往server，然后由server将\(T\)个client聚为\(S_1,...,S_k\)。然后对每一个类\(k(k\in [K])\)，运行传统联邦学习方法（如FedAvg^[5]或二阶方法^[6][7]）求解出最终的\(\hat{\theta}_k\)。注意, 此种方式默认每个聚类簇得到一个参数\(\hat{\theta}_k\)。同样，类似我们上面对一次性聚类多任务学习的分析，如果一旦开局的聚类算法产生了错误的估计，那么接下来的时间里算法将无法对其进行更正。而且，如果计算的是神经网络模型参数之间的距离，还会产生另外的问题，参见下文4.1部分。

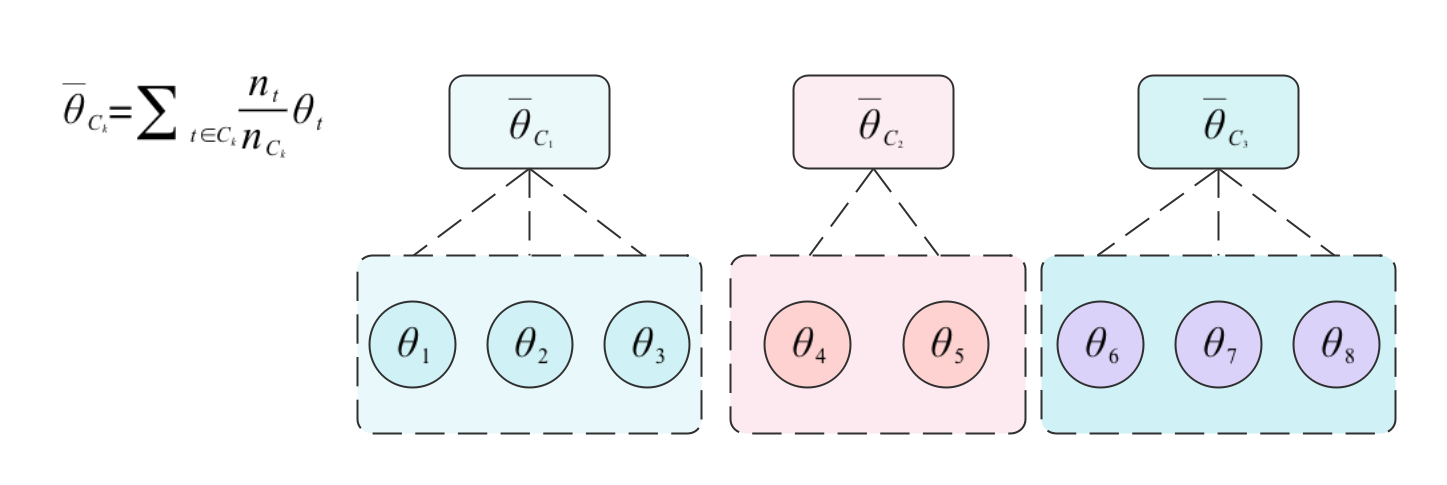
动态式的聚类为则为在训练的过程中一边训练，一边根据模型参数\(\widetilde{\theta}_t\)的情况来动态调整聚类结果。这种方式既可以簇内任务直接广播参数\(\theta_k\)，也可以仅仅共享参数的变化量\(\Delta \theta_k\)。

聚类联邦学习可以看做将一个簇视为一个学习任务。按照其对簇结构的潜在假设，可分为簇间知识共享和簇间不共享两种。簇间知识共享型构成比较标准的多任务学习，它的每个学习任务之间可以知识共享。而簇间不共享型不算标准的多任务学习，因为不同簇之间互不干扰，没有知识共享，不过也体现了“多任务”的思想，因此我们还是放在此处介绍。

4. 聚类联邦学习经典论文阅读 4.1 arXiv 2019:《Robust federated learning in a heterogeneous environment》^[11]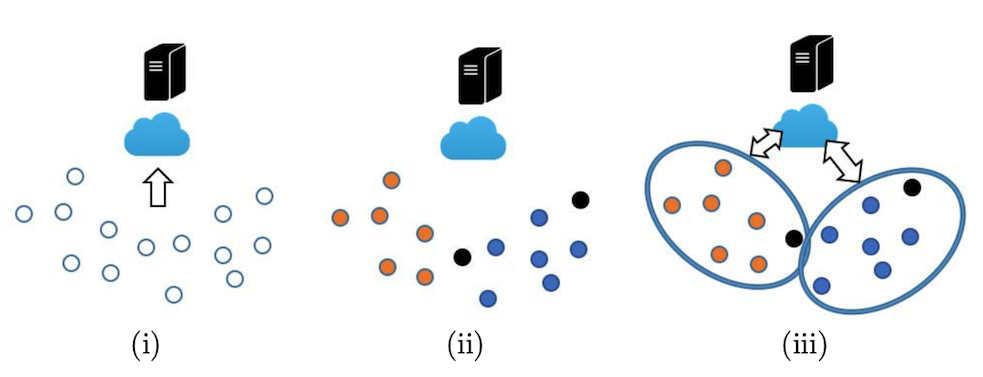

本文采用的是一次性聚类和簇间不共享。本论文需要事先指定聚类簇的个数\(K\)，然后在训练迭代开始前，常常将\(T\)个client初步训练后的参数\(\{\widetilde{\theta}_t\}^T_{t=1}\)发往server，然后由server运行K-means算法将\(T\)个client聚为\(S_1,...,S_k\)。然后对每一个类\(k(k\in [K])\)，单独运行传统联邦学习方法（如FedAvg^[5]或二阶方法^[6][7]）求解出最终的\(\hat{\theta}_k\)。注意, 此种方式默认每个聚类簇得到一个参数\(\hat{\theta}_k\)。该算法属于簇间不共享型，因为它的每个簇之间缺少知识共享。

然而，这种方法常常使用类似于K-means的距离聚类方法，而从理论上讲对于神经网络两个模型拥有相近的参数距离，但其输出可能大不相同（由于模型对于隐藏层单元的置换不变性）。而近期我做过实验，单纯比较神经网络之间的欧式/余弦距离来确定模型的相似性效果非常差，不建议大家采用。

4.2 TNNLS 2020:《Clustered Federated Learning: Model-Agnostic Distributed Multitask Optimization Under Privacy Constraints》^[8]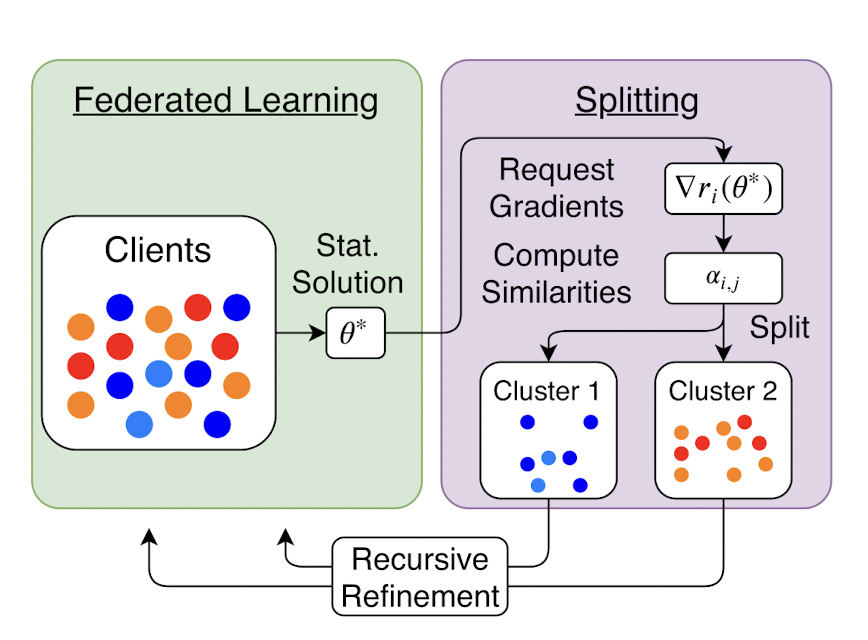

本文采用的是迭代式聚类和簇间不共享，它在每轮迭代时，都会根据节点的参数相似度进行一次类簇划分，同一个类簇共享参数的变化量 \(g\)，以此既能达到每个节点训练一个性化模型，又能完成数据相似的节点相互促进（知识共享），减少数据不相似节点之间的影响的目的。本论文的亮点是聚类簇的个数可以随着迭代变化，无需实现指定类簇个数\(K\)做为先验。

本篇论文算法的每轮通信描述如下：

(1) 第\(t\)个client节点执行

• 从server接收对应的簇参数\(g_k\)。
• 令\(\theta_{old}=\theta_t=\theta_t + g_k\)。
• 执行\(E\)个局部epoch的SGD：
  \[\theta_t = \theta_t - \eta \nabla \mathcal{l}(\theta_t; b) \]
  (此处将局部数据\(D_t\)划分为多个\(b\))
• 将\(\widetilde{g}_t = \theta_t-\theta_{old}\)发往server。
• 重置\(\theta_t = \theta_{old}\)。

(2) server节点执行

• 从\(T\)个client接收\(\widetilde{g}_1、\widetilde{g}_2,...\widetilde{g}_T\)。

• 对每一个簇\(k\)，计算簇内平均参数变化：

\[\hat{g}_{k} = \frac{1}{|S_k|}\sum_{t\in S_k}\widetilde{g}_t \]

• 将每个簇的簇内变化\(\hat{g}_k\)发往对应的client。

• 根据不同节点参数变化量的余弦距离\(\alpha_{i,j}=\frac{\langle \widetilde{g}_i, \widetilde{g}_j\rangle}{||\widetilde{g}_i||||\widetilde{g}_j||}\)重新划分聚类簇。

和4.1中的算法一样，它的每个簇之间缺少知识共享。

4.3 NIPS 2020:《An Efficient Framework for Clustered Federated Learning》^[8]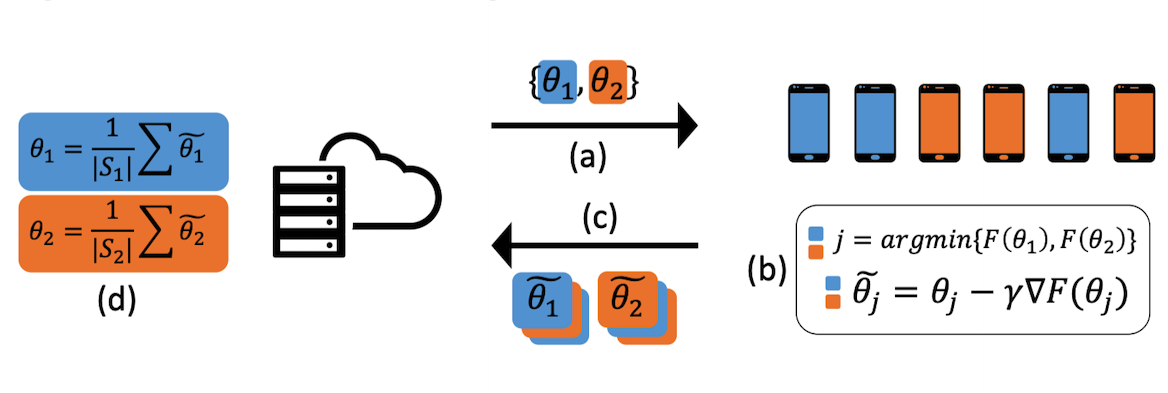

本文采用的是迭代式聚类和簇间共享。本论文需要事先指定聚类簇的个数\(K\)。其每个簇内的节点都共享一组平均参数，而它在每轮迭代时，都会通过损失函数最小化的手段为各节点重新估计其所属的簇（使用每个簇的平均参数）。此外，每轮迭代都会重新计算每个簇对应的参数平均值，第\(k\)个类簇对其所有节点广播参数\(\theta_k\)，也就是说每个聚类簇构成一个学习任务(负责学习属于该类簇的个性化模型)。

本篇论文算法的每轮通信描述如下：

(1) 第\(t\)个client节点执行

• 从server接收簇参数\(\theta_1,\theta_2,...\theta_{K}\)

• 估计其所属的簇：\(\hat{k}=\underset{k\in[K]}{\text{argmin }}\mathcal{l}(\theta_k;D_t)\)

• 对簇参数执行\(E\)个局部epoch的SGD：

  \[\theta_k = \theta_k - \eta \nabla \mathcal{l}(\theta_k; b) \]

  (此处将局部数据\(D_t\)划分为多个\(b\))

• 将最终得到的簇参数做为\(\widetilde{\theta}_t\)，并和该client对应的簇划分一起发往server。

(2) server节点执行

• 从\(T\)个client接收\(\widetilde{\theta}_1、\widetilde{\theta}_2,..., \widetilde{\theta}_T\)和各client的簇划分情况

• 根据节点参数的平均值来更新簇参数：

\[\hat{\theta}_k = \frac{1}{|S_k|} \sum_{t \in S_k}\widetilde{\theta}_t \]

由于现实的聚类关系很模糊，该算法在具体实现时效仿多任务学习中的权值共享^[1]机制，允许不同簇(任务)之间共享部分参数。具体地，即在训练神经网络模型时，先使用所有client的训练数据学习一个共享表示，然后再运行聚类算法为每个簇学习神经网络的最后一层（即多任务层），因此该算法是簇间共享型。

4.4 WWW 2021:《PFA: Privacy-preserving Federated Adaptation for Effective Model Personalization》^[9]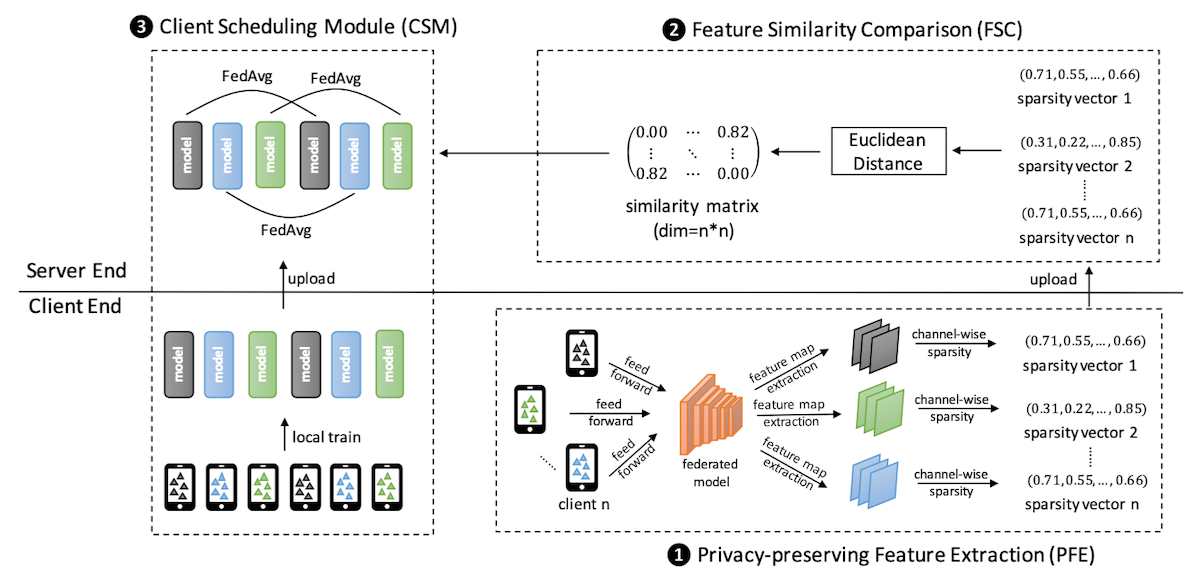

本文采用的是一次性聚类和簇间不共享。本论文需要事先指定聚类簇的个数\(K\)，然后在训练迭代开始前，每个节点先训练一个稀疏表征模型模型，然后将稀疏表征模型得到的稀疏向量传到server，server再根据各client稀疏向量之间的相似度进行类簇划分。之后，各类簇分别运行传统FedAvg算法学习每个簇对应的个性化模型。值得一提的是，和4.1、4.2中的算法一样，它的每个簇之间缺少知识共享。

4.5 INFOCOM 2021:《Resource-Efficient Federated Learning with Hierarchical Aggregation in Edge Computing》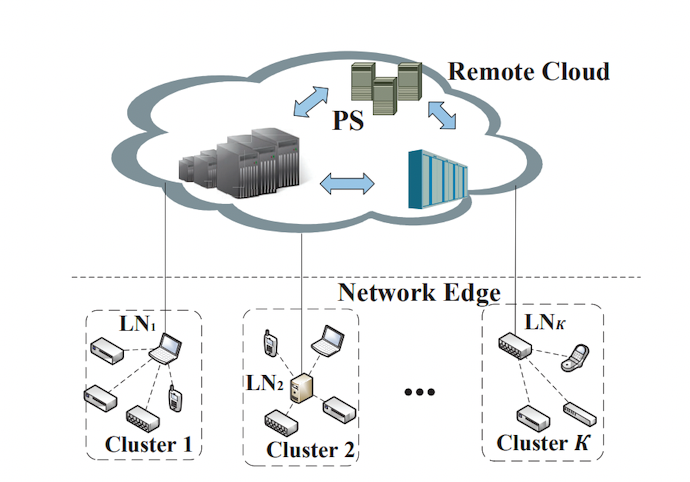

这篇文章严格来说不属于上面所说的聚类联邦学习，也缺少知识共享而不是多任务学习/个性化联邦学习的范畴。其文中提到的clustered应该翻译成"（局域网构成的）集群的"。但我觉得这篇文章算是从另一个工程的角度来应用了分组聚合的思想，我在这里还是觉得将其介绍一下。

在现实工业环境下，联邦学习常常是基于参数服务器(parameter server)的，但参数服务器位于远程云平台上，边缘节点与它之间的通信经常不可用，而边缘节点的数量庞大，这就导致通信代价可能会很高。本文的基本思想即是减少边缘节点和PS之间的通信，加强边缘节点之间的协作。论文将不同的client划分为了多个局域网/集群，每个集群都有一个leader node（LN）做为集群头。每个集群先分别运行FedAvg算法将参数聚合到LN(集群内是同步的)，然后再由PS异步地搜集各LN的参数并进行聚合。最后再将新的参数广播到各个边远client。

本篇论文还考虑了每个client的资源消耗等复杂信息，此处为了简单起见，我们将简化后算法的每轮通信描述如下：

(1) 第\(t\)个client节点执行

• 从\(LN_k\)接收参数\(\theta\)做为本地的\(\theta_t\)
• 执行\(E\)个局部epoch的SGD：
  \[\theta_t = \theta_t - \eta \nabla \mathcal{l}(\theta_t; b) \]
  (此处将局部数据\(D_t\)划分为多个\(b\))
• 将新的参数\(\widetilde{\theta}_t\)发往所在簇的\(LN_k\)。

(2) \(LN_k\)节点执行

• 从集群内的\(|S_k|\)个client接收参数\(\{\widetilde{\theta}_j\}(j\in S_k)\)

• 根据簇内节点参数的加权平均值来更新簇参数：

\[\theta_k = \frac{\sum_{j \in S_k}{ |D_j|}\widetilde{\theta}_j}{\sum_{j\in S_k} |D_j|} \]

• 将簇参数\(\theta_k\)发往PS。
• 从PS接收参数\(\theta\)并将其发往client节点。

(2) PS节点执行

• 从\(k\)个\(LN_k\)节点接收\({\theta}_k\)（异步地）。

• 根据一阶指数平滑来更新参数：

\[\hat{\theta} = (1-\alpha)\theta + \alpha \theta_k \]

\(\quad\quad\)(在实际论文中\(\alpha\)是一个在迭代中变化的量，此处为了简化省略)

• 将新的参数\(\hat{\theta}\)发往\(LN_k\)

引用

• [1] Caruana R. Multitask learning[J]. Machine learning, 1997, 28(1): 41-75

• [2] Thrun S, O'Sullivan J. Discovering structure in multiple learning tasks: The TC algorithm[C]//ICML. 1996, 96: 489-497.

• [3] Bakker B J, Heskes T M. Task clustering and gating for bayesian multitask learning[J]. 2003.

• [4] Sattler F, Müller K R, Samek W. Clustered federated learning: Model-agnostic distributed multitask optimization under privacy constraints[J]. IEEE transactions on neural networks and learning systems, 2020, 32(8): 3710-3722.

• [5] McMahan B, Moore E, Ramage D, et al. Communication-efficient learning of deep networks from decentralized data[C]//Artificial intelligence and statistics. PMLR, 2017: 1273-1282.

• [6] Wang S, Roosta F, Xu P, et al. Giant: Globally improved approximate newton method for distributed optimization[J]. Advances in Neural Information Processing Systems, 2018, 31.

• [7] Ghosh A, Maity R K, Mazumdar A. Distributed newton can communicate less and resist byzantine workers[J]. Advances in Neural Information Processing Systems, 2020, 33: 18028-18038.

• [8] Ghosh A, Chung J, Yin D, et al. An efficient framework for clustered federated learning[J]. Advances in Neural Information Processing Systems, 2020, 33: 19586-19597.

• [9] Liu B, Guo Y, Chen X. PFA: Privacy-preserving Federated Adaptation for Effective Model Personalization[C]//Proceedings of the Web Conference 2021. 2021: 923-934.

• [10] Wang Z, Xu H, Liu J, et al. Resource-Efficient Federated Learning with Hierarchical Aggregation in Edge Computing[C]//IEEE INFOCOM 2021-IEEE Conference on Computer Communications. IEEE, 2021: 1-10.

• [11] Ghosh A, Hong J, Yin D, et al. Robust federated learning in a heterogeneous environment[J]. arXiv preprint arXiv:1906.06629, 2019.

数学是符号的艺术，音乐是上界的语言。