1、定义假设函数 \(h(x) = \theta_1x + \theta_0\)
2、尝试用样本拟合假设函数,所有样本点到假设函数的距离,其中\(m\)为样本数量:
\[sum = \dfrac{1}{2m} \sum_{1}^{m} (h(x_i) - y_i)^2 \]3、当 sum 的值越小,假设函数的偏差就预测样本更加精确。这个表达式就是代价函数 \(j(\theta)\) ,目标就是最小化代价函数的值。
4、假设 \(h(x)\) 没有常数项 \(\theta_0\) , \(h(x)\) 将会会是一个从原点出发的直线,不断变动 \(\theta_1\) 的值(斜率),带入样本 \((1, 1), (2, 2) , (3, 3)\) 可以发现代价函数 \(j(\theta)\)是一个二次函数,并且在值为 1 的时候,代价函数 \(h(x)\) 的值最小。
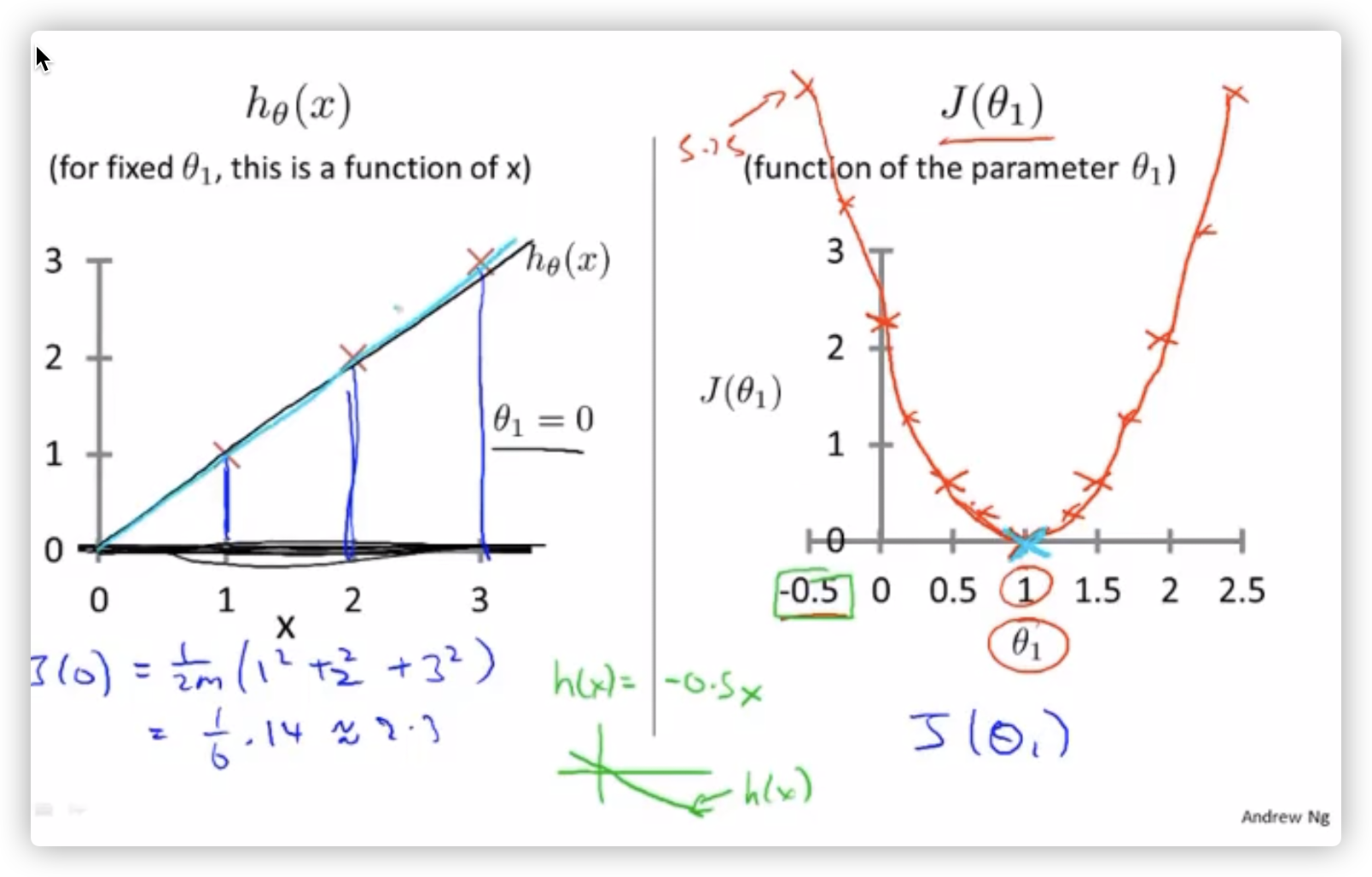
问题:为了将代价函数最小化,但是代价函数\(J(\theta)\)在多维后不能可视化,所以需要一种方法来求得最小值。
梯度下降算法描述:

对于每一个 \(\theta_i\) 参数,不断减去代价函数\(j(\theta_0 \cdots \theta_n)\) 对 \(\theta_i\) 的偏导和学习率 \(a\) ,直到收敛,收敛的意思是导数项为0,\(\theta_i\) 的值不再发生变化。
线性回归的梯度下降的代价函数总是一个凸函数,没有局部最优解,只有全局最优解。
学习率的取值1、学习率太大收敛不了,梯度下降的过程中,不断跳过最低点,需要适当调小学习率;
2、太小的话学习速度太慢
3、学习率总能到达局部最低点,即使学习率是固定的,因为接近最低解的时候,导数会自动变化。
4、调试梯度下降,保证梯度下降是在正确运行要求是每次迭代都需要降低 \(J(\theta)\) 的值,设定收敛阈值 \(\sigma\) 。
多元线性回归当处理的问题的特征输入变成多个时,假设函数将会变成:
\[h(x) = \theta_0x_0 + \theta_1x_1 + \cdots + \theta_nx_n \]其中 \(x_0\) = 1。
如果假设两个矩阵:
\[X = \begin{bmatrix} x_0 \\ x_1 \\ \cdots \\ x_n \end{bmatrix}, \Theta= \begin{bmatrix} \theta_0 \\ \theta_1 \\ \cdots \\ \theta_n \end{bmatrix} \]那么假设函数就能表示为:
\[h(x) = \Theta^TX \]特征缩放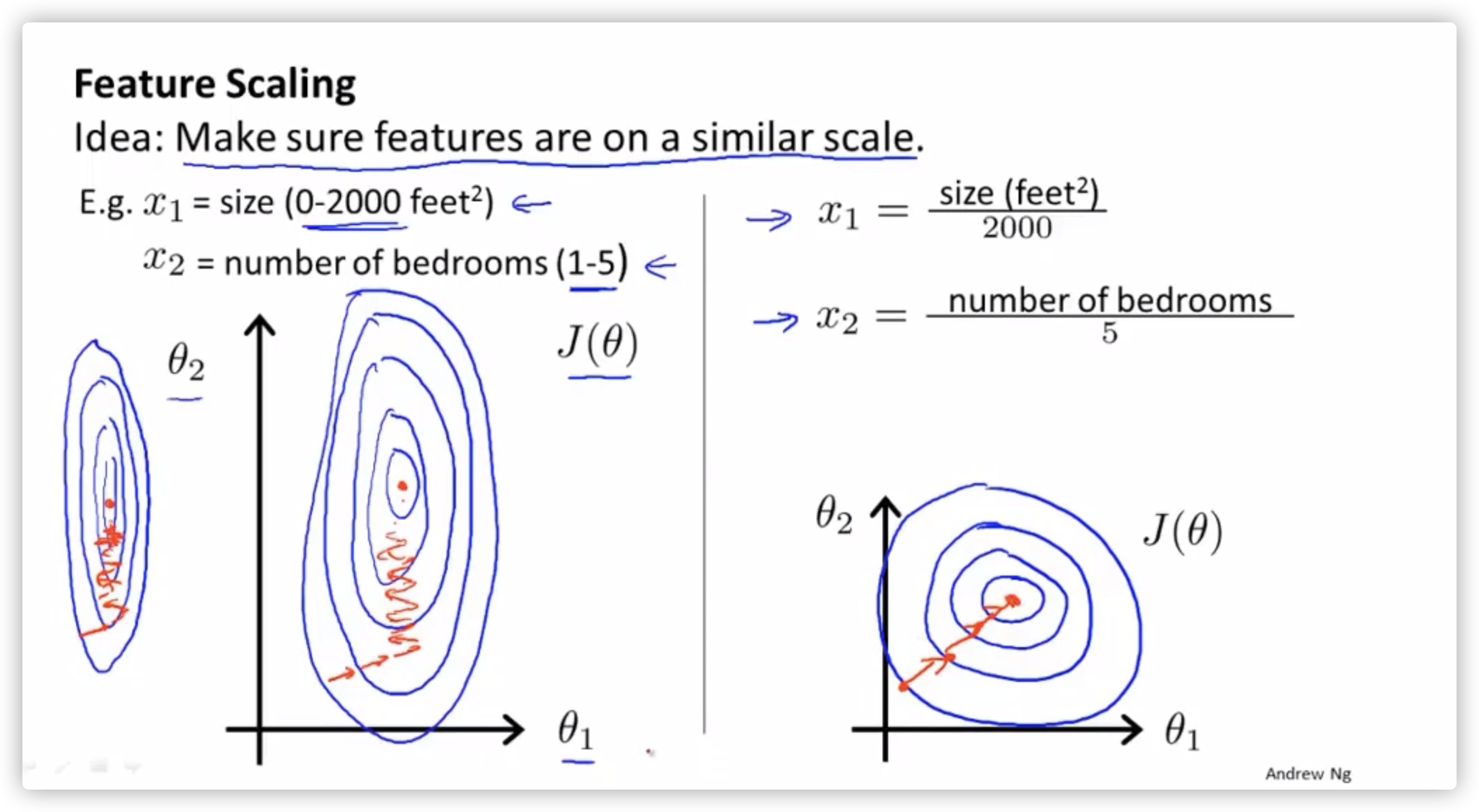
将特征的值放到相同的规模上,如果不在同一规模,有可能要梯度下降很久。
面对这种问题,经验是将特征缩放到 -1 ~ 1 之间。
缩放的方法:均值归一化,特征值减去平均值除以特征的范围。
正规方程求解除了梯度下降的方法找到最优点,还可以直接通过求导数值为0的点计算出结果。当
\[J(\theta_0, \theta_1, \cdots, \theta_m) = \dfrac{1}{2m} \sum_{1}^{m} (h(x_i) - y_i)^2 \]只要代价函数求得对每个 \(\theta\) 的偏导的值为 0 的点即可。
\[\dfrac{\partial}{\partial\theta_j} J(\theta_0, \theta_1, \cdots, \theta_m) = \cdots = 0 \]正规方程在求解大特征的时候需要求转置和矩阵的逆,但是在n小的时候求得比较快。(特征少的时候选择)。
