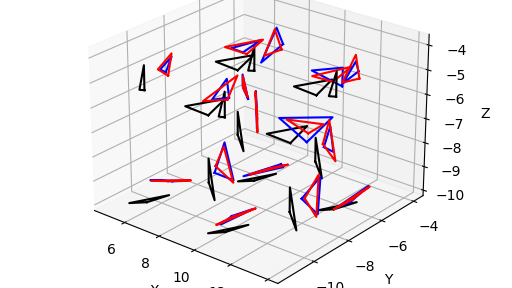
 在前一篇文章中介绍了SETTLE约束算法在分子动力学模拟中的应用,本文通过用Jax的Vmap功能对SETTLE函数进行了扩维,使得其可以批量的计算多分子体系的约束条件。这里采用的案例是一个含有16个水分子(48原子)的小体系,从结果中可以看到,在随机移动和批量SETTLE的作用下,所有的水分子都保留了原始的键长和键角,简单理解这个过程就是一个刚体三角形的平移和旋转的过程。
技术背景
在前一篇文章中介绍了SETTLE约束算法在分子动力学模拟中的应用,本文通过用Jax的Vmap功能对SETTLE函数进行了扩维,使得其可以批量的计算多分子体系的约束条件。这里采用的案例是一个含有16个水分子(48原子)的小体系,从结果中可以看到,在随机移动和批量SETTLE的作用下,所有的水分子都保留了原始的键长和键角,简单理解这个过程就是一个刚体三角形的平移和旋转的过程。
技术背景
在上一篇文章中,我们介绍了在分子动力学模拟中SETTLE约束算法的实现与应用,其中更多的是针对于单个的水分子。但由于相关代码是通过jax这一框架来实现的,因此对于多分子的体系,可以采用jax所支持的vmap来实现,简单快捷。同时为了模块化的编程,本文中的代码相对于上一篇文章做了函数封装,也更符合jax这种函数化编程的风格。
构建多分子体系本文使用的是一个16个水分子这样的一个体系,pdb文件内容如下所示:
CRYST1 9.039 7.826 7.379 90.00 90.00 90.00 P 1 1
ATOM 1 O X 1 10.189 -10.483 -5.440 0.00 0.00 O
ATOM 2 H1 X 1 10.185 -10.473 -4.440 0.00 0.00 H
ATOM 3 H2 X 1 9.374 -10.015 -5.781 0.00 0.00 H
ATOM 4 O X 1 7.933 -9.186 -6.385 0.00 0.00 O
ATOM 5 H1 X 1 7.115 -9.655 -6.049 0.00 0.00 H
ATOM 6 H2 X 1 7.931 -8.241 -6.059 0.00 0.00 H
ATOM 7 O X 1 7.929 -6.569 -5.486 0.00 0.00 O
ATOM 8 H1 X 1 7.925 -6.559 -4.486 0.00 0.00 H
ATOM 9 H2 X 1 7.114 -6.101 -5.827 0.00 0.00 H
ATOM 10 O X 1 10.193 -5.274 -6.412 0.00 0.00 O
ATOM 11 H1 X 1 9.375 -5.741 -6.077 0.00 0.00 H
ATOM 12 H2 X 1 10.191 -4.327 -6.087 0.00 0.00 H
ATOM 13 O X 1 12.449 -6.569 -5.468 0.00 0.00 O
ATOM 14 H1 X 1 12.445 -6.559 -4.468 0.00 0.00 H
ATOM 15 H2 X 1 11.633 -6.101 -5.809 0.00 0.00 H
ATOM 16 O X 1 12.453 -9.186 -6.366 0.00 0.00 O
ATOM 17 H1 X 1 11.634 -9.655 -6.031 0.00 0.00 H
ATOM 18 H2 X 1 12.451 -8.241 -6.041 0.00 0.00 H
ATOM 19 O X 1 10.207 -10.526 -10.053 0.00 0.00 O
ATOM 20 H1 X 1 10.206 -11.466 -9.710 0.00 0.00 H
ATOM 21 H2 X 1 11.022 -10.052 -9.720 0.00 0.00 H
ATOM 22 O X 1 7.944 -9.212 -9.151 0.00 0.00 O
ATOM 23 H1 X 1 7.940 -9.203 -8.151 0.00 0.00 H
ATOM 24 H2 X 1 8.762 -9.688 -9.477 0.00 0.00 H
ATOM 25 O X 1 7.947 -6.612 -10.099 0.00 0.00 O
ATOM 26 H1 X 1 7.946 -7.552 -9.756 0.00 0.00 H
ATOM 27 H2 X 1 8.763 -6.138 -9.766 0.00 0.00 H
ATOM 28 O X 1 10.204 -5.300 -9.179 0.00 0.00 O
ATOM 29 H1 X 1 10.200 -5.290 -8.179 0.00 0.00 H
ATOM 30 H2 X 1 11.021 -5.774 -9.504 0.00 0.00 H
ATOM 31 O X 1 12.467 -6.612 -10.081 0.00 0.00 O
ATOM 32 H1 X 1 12.466 -7.552 -9.738 0.00 0.00 H
ATOM 33 H2 X 1 13.282 -6.138 -9.748 0.00 0.00 H
ATOM 34 O X 1 12.464 -9.212 -9.133 0.00 0.00 O
ATOM 35 H1 X 1 12.460 -9.203 -8.133 0.00 0.00 H
ATOM 36 H2 X 1 13.281 -9.687 -9.458 0.00 0.00 H
ATOM 37 O X 1 5.670 -10.483 -5.458 0.00 0.00 O
ATOM 38 H1 X 1 5.666 -10.473 -4.459 0.00 0.00 H
ATOM 39 H2 X 1 4.854 -10.015 -5.799 0.00 0.00 H
ATOM 40 O X 1 5.688 -10.526 -10.071 0.00 0.00 O
ATOM 41 H1 X 1 5.687 -11.466 -9.728 0.00 0.00 H
ATOM 42 H2 X 1 6.503 -10.052 -9.738 0.00 0.00 H
ATOM 43 O X 1 5.674 -5.274 -6.430 0.00 0.00 O
ATOM 44 H1 X 1 4.855 -5.742 -6.095 0.00 0.00 H
ATOM 45 H2 X 1 5.672 -4.328 -6.105 0.00 0.00 H
ATOM 46 O X 1 5.685 -5.300 -9.197 0.00 0.00 O
ATOM 47 H1 X 1 5.681 -5.290 -8.197 0.00 0.00 H
ATOM 48 H2 X 1 6.502 -5.774 -9.523 0.00 0.00 H
END
有了这样的一个体系之后,当我们需要扩展这个体系,也可以仅把这个体系平移repeat一份即可。
批量处理代码实现关于这里的算法和代码的解析,还是推荐看下上一篇文章中所讲述的内容,这里就直接展示一下更新之后的代码:
# batch_settle.py
from jax import numpy as np
from jax import vmap, jit
def rotation(psi,phi,theta,v):
""" Module of rotation in 3 Euler angles. """
RY = np.array([[np.cos(psi),0,-np.sin(psi)],
[0, 1, 0],
[np.sin(psi),0,np.cos(psi)]])
RX = np.array([[1,0,0],
[0,np.cos(phi),-np.sin(phi)],
[0,np.sin(phi),np.cos(phi)]])
RZ = np.array([[np.cos(theta),-np.sin(theta),0],
[np.sin(theta),np.cos(theta),0],
[0,0,1]])
return np.dot(RZ,np.dot(RX,np.dot(RY,v)))
multi_rotation = jit(vmap(rotation,(None,None,None,0)))
def get_rot(crd):
""" Get the coordinates transform matrix. """
# get the center of mass
com = np.average(crd, 0)
rc = np.linalg.norm(crd[2]-crd[1])/2
ra = np.linalg.norm(crd[0]-com)
rb = np.sqrt(np.linalg.norm(crd[2]-crd[0])**2-rc**2)-ra
# 3 points are selected to solve the initial rotation matrix
xyz = [0, 0, 0]
xyz[0] = crd[0] - com
xyz[1] = crd[1] - com
cross = np.cross(crd[2] - crd[1], crd[0] - crd[2])
cross /= np.linalg.norm(cross)
xyz[2] = cross
xyz = np.array(xyz)
inv_xyz = np.linalg.inv(xyz)
v0 = np.array([0, -rc, 0])
v1 = np.array([ra, -rb, 0])
v2 = np.array([0, 0, 1])
# final rotation matrix is constructed by following
Rot = np.array([np.dot(inv_xyz, v0), np.dot(inv_xyz, v1), np.dot(inv_xyz, v2)])
inv_Rot = np.linalg.inv(Rot)
return Rot, inv_Rot
def xyzto(Rot, crd, com):
""" Apply the coordinates transform matrix. """
return np.dot(Rot, crd-com)
multi_xyzto = jit(vmap(xyzto,(None,0,None)))
def toxyz(Rot, crd, com):
""" Apply the inverse of transform matrix. """
return np.dot(Rot, crd-com)
multi_toxyz = jit(vmap(toxyz,(None,0,None)))
def get_circumference(crd):
""" Get the circumference of all triangles. """
return np.linalg.norm(crd[0]-crd[1])+np.linalg.norm(crd[0]-crd[2])+np.linalg.norm(crd[1]-crd[2])
jit_get_circumference = jit(get_circumference)
def get_angles(crd_0, crd_t0, crd_t1):
""" Get the rotation angle psi, phi and theta. """
com = np.average(crd_0, 0)
rc = np.linalg.norm(crd_0[2] - crd_0[1]) / 2
ra = np.linalg.norm(crd_0[0] - com)
rb = np.sqrt(np.linalg.norm(crd_0[2] - crd_0[0]) ** 2 - rc ** 2) - ra
phi = np.arcsin(crd_t1[0][2]/ra)
psi = np.arcsin((crd_t1[1][2]-crd_t1[2][2])/2/rc/np.cos(phi))
alpha = -rc*np.cos(psi)*(crd_t0[1][0]-crd_t0[2][0])+(-rb*np.cos(phi)-rc*np.sin(psi)*np.sin(phi))*(crd_t0[1][1]-crd_t0[0][1])+ \
(-rb*np.cos(phi)+rc*np.sin(psi)*np.sin(phi))*(crd_t0[2][1]-crd_t0[0][1])
beta = -rc*np.cos(psi)*(crd_t0[2][1]-crd_t0[1][1])+(-rb*np.cos(phi)-rc*np.sin(psi)*np.sin(phi))*(crd_t0[1][0]-crd_t0[0][0])+ \
(-rb*np.cos(phi)+rc*np.sin(psi)*np.sin(phi))*(crd_t0[2][0]-crd_t0[0][0])
gamma = crd_t1[1][1]*(crd_t0[1][0]-crd_t0[0][0])-crd_t1[1][0]*(crd_t0[1][1]-crd_t0[0][1])+\
crd_t1[2][1]*(crd_t0[2][0]-crd_t0[0][0])-crd_t1[2][0]*(crd_t0[2][1]-crd_t0[0][1])
sin_part = gamma/np.sqrt(alpha**2+beta**2)
theta = np.arcsin(sin_part)-np.arctan(beta/alpha)
return phi, psi, theta
jit_get_angles = jit(get_angles)
def get_d3(crd_0, psi, phi, theta):
""" Calculate the new coordinates by 3 given angles. """
com = np.average(crd_0, 0)
rc = np.linalg.norm(crd_0[2] - crd_0[1]) / 2
ra = np.linalg.norm(crd_0[0] - com)
rb = np.sqrt(np.linalg.norm(crd_0[2] - crd_0[0]) ** 2 - rc ** 2) - ra
return np.array([[-ra*np.cos(phi)*np.sin(theta), ra*np.cos(phi)*np.cos(theta), ra*np.sin(phi)],
[-rc*np.cos(psi)*np.cos(theta)+rb*np.sin(theta)*np.cos(phi)+rc*np.sin(theta)*np.sin(psi)*np.sin(phi),
-rc*np.cos(psi)*np.sin(theta)-rb*np.cos(theta)*np.cos(phi)-rc*np.cos(theta)*np.sin(psi)*np.sin(phi),
-rb*np.sin(phi)+rc*np.sin(psi)*np.cos(phi)],
[rc*np.cos(psi)*np.cos(theta)+rb*np.sin(theta)*np.cos(phi)-rc*np.sin(theta)*np.sin(psi)*np.sin(phi),
rc*np.cos(psi)*np.sin(theta)-rb*np.cos(theta)*np.cos(phi)+rc*np.cos(theta)*np.sin(psi)*np.sin(phi),
-rb*np.sin(phi)-rc*np.sin(psi)*np.cos(phi)]])
jit_get_d3 = jit(get_d3)
def settle(crd_0, crd_1):
com_0 = np.average(crd_0, 0)
com_1 = np.average(crd_1, 0)
# get the coordinate transform matrix and correspond inverse operation
rot, inv_rot = get_rot(crd_0)
crd_t0 = multi_xyzto(rot, crd_0, com_0)
com_t0 = np.average(crd_t0, 0)
crd_t1 = multi_xyzto(rot, crd_1, com_1) + com_1
com_t1 = np.average(crd_t1, 0)
phi, psi, theta = jit_get_angles(crd_0, crd_t0, crd_t1 - com_t1)
crd_t3 = jit_get_d3(crd_t0, psi, phi, theta) + com_t1
com_t3 = np.average(crd_t3, 0)
crd_3 = multi_toxyz(inv_rot, crd_t3, com_t3) + com_1
return crd_3
jit_settle = jit(settle)
batch_settle = jit(vmap(settle,(0,0)))
def crd_from_pdb(pdb_name, repeat=0):
with open(pdb_file) as pdb:
lines = pdb.readlines()
length = len(lines)
atoms = 3
crd_0 = []
for i in range(int((length-2)/atoms)):
this_crd = []
O = lines[i*atoms+1].split()[5:8]
this_crd.append([float(xyz) for xyz in O])
H1 = lines[i * atoms + 2].split()[5:8]
this_crd.append([float(xyz) for xyz in H1])
H2 = lines[i * atoms + 3].split()[5:8]
this_crd.append([float(xyz) for xyz in H2])
crd_0.append(this_crd)
crd_0 = np.array(crd_0)
crd_repeat = crd_0.copy()
for _ in range(repeat):
for crd in crd_0:
crd_repeat = np.append(crd_repeat, (crd+repeat)[None,:], axis=0)
return crd_repeat
def plot_atoms(crd_0, crd_1, crd_3):
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for batch in range(crd_0.shape[0]):
x_0 = np.append(crd_0[batch, :, 0], crd_0[batch][0][0])
y_0 = np.append(crd_0[batch, :, 1], crd_0[batch][0][1])
z_0 = np.append(crd_0[batch, :, 2], crd_0[batch][0][2])
ax.plot(x_0, y_0, z_0, color='black')
x_1 = np.append(crd_1[batch, :, 0], crd_1[batch][0][0])
y_1 = np.append(crd_1[batch, :, 1], crd_1[batch][0][1])
z_1 = np.append(crd_1[batch, :, 2], crd_1[batch][0][2])
ax.plot(x_1, y_1, z_1, color='blue')
x_3 = np.append(crd_3[batch, :, 0], crd_3[batch][0][0])
y_3 = np.append(crd_3[batch, :, 1], crd_3[batch][0][1])
z_3 = np.append(crd_3[batch, :, 2], crd_3[batch][0][2])
ax.plot(x_3, y_3, z_3, color='red')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
def plot_time_scale(x, y):
import matplotlib.pyplot as plt
plt.figure()
plt.plot(x, y, '-o', color='black')
plt.show()
if __name__ == '__main__':
import numpy as onp
onp.random.seed(0)
# Read coordinates from pdb file
pdb_file = 'cell.pdb'
crd_0 = crd_from_pdb(pdb_file, repeat=0)
print (crd_0)
# Construct an initial move
vel = np.array(onp.random.random(crd_0.shape))
dt = 1
# get the unconstraint crd
crd_1 = crd_0 + vel * dt
crd_3 = batch_settle(crd_0, crd_1)
# Plotting
plot_atoms(crd_0, crd_1, crd_3)
其中主要的改进之处,在于增加了batch_settle = jit(vmap(settle,(0,0)))这样的vmap函数构造形式,其中(0,0)表示的是针对于输入的两个坐标的第0个维度进行扩展。也就是说,只要写一个分子的处理方式,就可以直接用这样的方式把算法推广到多个分子的处理方式上。同时在最外层封装了一个即时编译jit函数,使得整体算法运行的效率更高。该代码运行的结果如下所示:
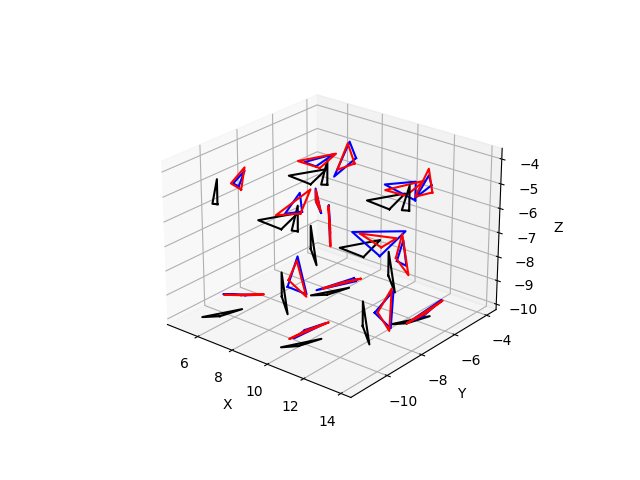
从结果中我们发现,所有的分子经过settle算法的约束,都回到了原本的键长键角,并且配合velocity-verlet算法可以实现施加约束条件的动力学模拟。这里假如我们调整参数repeat=5,得到的结果如下:
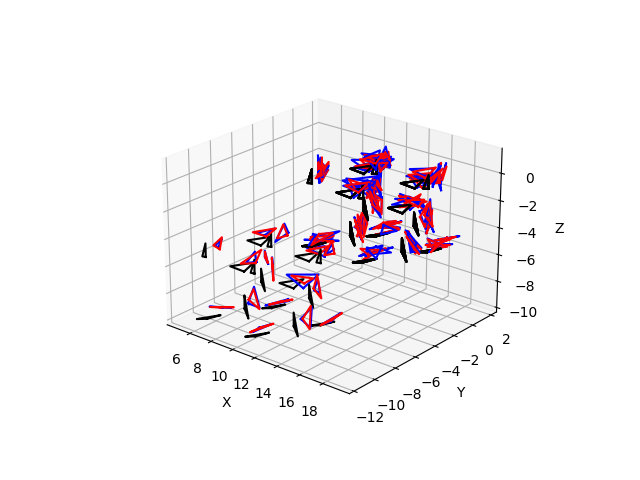
这样我们就得到了一个更大的体系的结果。
总结概要在前一篇文章中介绍了SETTLE约束算法在分子动力学模拟中的应用,本文通过用Jax的Vmap功能对SETTLE函数进行了扩维,使得其可以批量的计算多分子体系的约束条件。这里采用的案例是一个含有16个水分子(48原子)的小体系,从结果中可以看到,在随机移动和批量SETTLE的作用下,所有的水分子都保留了原始的键长和键角,简单理解这个过程就是一个刚体三角形的平移和旋转的过程。
版权声明本文首发链接为:https://www.cnblogs.com/dechinphy/p/batch-settle.html
作者ID:DechinPhy
更多原著文章请参考:https://www.cnblogs.com/dechinphy/
打赏专用链接:https://www.cnblogs.com/dechinphy/gallery/image/379634.html
腾讯云专栏同步:https://cloud.tencent.com/developer/column/91958
参考链接- https://www.cnblogs.com/dechinphy/p/settle.html
