联邦学习：按混合分布划分Non-IID样本

在上一篇博文中我们已经提到了按照Dirichlet分布划分联邦学习Non-IID数据集的一种算法。下面让我们来看按Dirichlet分布划分数据集的另外一种变种，即按混合分布划分Non-IID样本，该方法在NIPS2021的一篇论文中首次提出。该论文提出了一个重要的假设，那就是虽然联邦学习每个client的数据是Non-IID，但我们假设它们都来自一个混合分布(混合成分个数为超参数可调。

我们在博文《联邦学习：按病态独立同分布划分Non-IID样本》中学习了联邦学习开山论文^[1]中按照病态独立同分布（Pathological Non-IID）划分样本。 在上一篇博文《联邦学习：按Dirichlet分布划分Non-IID样本》中我们也已经提到了按照Dirichlet分布划分联邦学习Non-IID数据集的一种算法。下面让我们来看按Dirichlet分布划分数据集的另外一种变种，即按混合分布划分Non-IID样本，该方法为论文^[2]中首次提出。

该论文采取了一个重要的假设，那就是虽然联邦学习每个client的数据是Non-IID的，但我们假设每个client的数据都来自于某个混合分布(混合成分个数\(K\)为超参数可调)。

\[p(x|\theta_t) = \sum_{k=1}^Kz_{tk} p(x|\theta_{k}) \]

其中\(t\)意思为第\(t\)个client，\(z_{tk}\)为（不可观测的）隐变量(latent variable)，意为第\(t\)个client中的数据来自成分\(k\)的概率。第\(t\)个client的某个样本点\(x\)进行生成时，会从\(K\)个成分中选择一个成分\(p(x|\theta_{k})\)进行采样，选择该成分的概率为\(\alpha_{tk}\)。

形象化的展示图片如下：

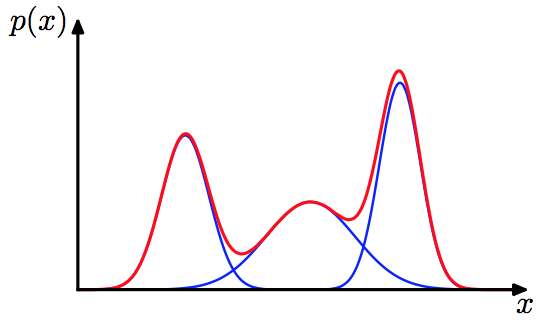
有了这个假设， 那么每个client的数据都可以视为来自这三个分布的数据的混合（每个client的Non-IID区别只是混合比例系数各不相同而已，下面我们提到混合比例系数由Dirichlet分布随机生成），那我们相当于假定了每个client数据间的一种"相似性"，即在各节点数据表面的Non-IID（\(p(x|\theta_t)\)）中其实潜藏IID的成分(\(p(x|\theta_{k}),k=1,2,..K\))。经过我的实验，一旦这样划分数据，那么对于基准的个性化联邦学习算法都会提升精度， 但是^[2]作者提出了一种基于子模型集成的算法来更加充分地利用这种相似性。比如，假设一个client一共有A、B、C这3个子成分， 那么我们就设计三个子模型分别对这些成分进行学习，每个模型的参数可以作为成分数据分布参数的一种体现。对于隐变量\(z_{tk}\)(做为子模型加权使用)，作者设计了EM算法来进行推断。

注意，这里作者的思想让我们联想到高斯混合分布。高斯混合分布就假设每个节点的数据采样自高斯混合分布中的一个成分(对应一个聚类簇)，而经典的高斯混合聚类就是要确定每个节点和簇的的对应关系（并推断出隐变量系数）, 可以参见我的博客《统计学习：EM算法及其在高斯混合模型(GMM)中的应用》。

接下来我们来看这个划分算法的函数如何设计。除了常规Dirichlet划分算法所要求的n_clients、n_classes、alpha等， 它还有一个专门的n_clusters参数，表示混合成分个数。我们来看函数原型：

def mixture_distribution_split_noniid(dataset, n_classes, n_clients, n_clusters, alpha):

我们解释一下函数的参数，这里dataset是torch.utils.Dataset类型的数据集，n_classes表示数据集里样本分类数，n_clusters是簇的个数（后面会解释其含义，如果设置为-1，则就默认n_clusters=n_classes，即每个簇对应一个标签类别），alpha 为Dirichlet分布参数，用于控制clients之间的数据diversity（Non-IID多样性）。该函数返回一个由n_client个client所需的样本索引组成的列表组成的列表client_idcs。

接下来我们看这个函数的内容。这个函数的内容可以概括为：先将所有类别不重叠地划分为n_clusters个簇（每个簇对应一个不同的标签分布，体现为标签不重叠）；再对每个簇c，将样本按照Non-IID划分给不同的clients（每个client的样本数量按照dirichlet分布来确定）。

首先，我们判断n_clusters的数量，如果为-1，则默认每一个cluster对应一个数据class：

    if n_clusters == -1:
        n_clusters = n_classes

然后将打乱后的标签集合\(\{0,1,...,n\_classes-1\}\)分为n_clusters个簇。注意，这就意为着每个簇对应的标签集合没有重叠，也就是说各个簇之间的样本数据是Non-IID的。

    all_labels = list(range(n_classes))
    np.random.shuffle(all_labels)
    def avg_divide(l, g):
        """
        将列表`l`分为`g`个独立同分布的group（其实就是直接划分）
        每个group都有 `int(len(l)/g)` 或者 `int(len(l)/g)+1` 个元素
        返回由不同的groups组成的列表
        """
        num_elems = len(l)
        group_size = int(len(l) / g)
        num_big_groups = num_elems - g * group_size
        num_small_groups = g - num_big_groups
        glist = []
        for i in range(num_small_groups):
            glist.append(l[group_size * i: group_size * (i + 1)])
        bi = group_size * num_small_groups
        group_size += 1
        for i in range(num_big_groups):
            glist.append(l[bi + group_size * i:bi + group_size * (i + 1)])
        return glist
    clusters_labels = avg_divide(all_labels, n_clusters)

然后再根据上面划分好的label集合建立key为label, value为簇id(group_idx)的字典，

    label2cluster = dict()  # maps label to its cluster
    for group_idx, labels in enumerate(clusters_labels):
        for label in labels:
            label2cluster[label] = group_idx

接着获取数据集的索引

    data_idcs = list(range(len(dataset)))

之后，我们将根据样本的label和前面建立的label->cluster映射，再将样本划分到对应簇里。

    # 记录每个cluster大小的向量
    clusters_sizes = np.zeros(n_clusters, dtype=int)
    # 存储每个cluster对应的数据索引
    clusters = {k: [] for k in range(n_clusters)}
    for idx in data_idcs:
        _, label = dataset[idx]
        # 由样本数据的label先找到其cluster的id
        group_id = label2cluster[label]
        # 再将对应cluster的大小+1
        clusters_sizes[group_id] += 1
        # 将样本索引加入其cluster对应的列表中
        clusters[group_id].append(idx)

    # 将每个cluster对应的样本索引列表打乱
    for _, cluster in clusters.items():
        rng.shuffle(cluster)

我们已经得到了属于每个cluster的样本索引，接着我们按照Dirichlet分布再将每个cluster中的样本Non-IID地划分到各client上去。

    # 记录某个cluster的样本分到某个client上的数量
    clients_counts = np.zeros((n_clusters, n_clients), dtype=np.int64) 

    # 遍历每一个cluster
    for cluster_id in range(n_clusters):
        # 对每个client赋予一个满足dirichlet分布的权重，用于该cluster样本的分配
        weights = np.random.dirichlet(alpha=alpha * np.ones(n_clients))
        # np.random.multinomial 表示投掷骰子clusters_sizes[cluster_id](该cluster中的样本数)次，落在各client上的权重依次是weights
        # 该函数返回落在各client上各多少次，也就对应着各client应该分得来自该cluster的样本数
        clients_counts[cluster_id] = np.random.multinomial(clusters_sizes[cluster_id], weights)

    # 对每一个cluster上的每一个client的计数次数进行前缀（累加）求和，
    # 相当于最终返回的是每一个cluster中按照client进行划分的样本分界点下标
    clients_counts = np.cumsum(clients_counts, axis=1)

然后，我们根据上面已经得到的属于各cluster的样本集合，和各cluster中样本分到各client中的情况（我们已经得到了每一个cluster中按照client进行划分的样本分界点下标），合并归纳得到每一个client中分得的样本情况。

    def split_list_by_idcs(l, idcs):
        """
        将列表`l` 划分为长度为 `len(idcs)` 的子列表
        第`i`个子列表从下标 `idcs[i]` 到下标`idcs[i+1]`
        （从下标0到下标`idcs[0]`的子列表另算）
        返回一个由多个子列表组成的列表
        """
        res = []
        current_index = 0
        for index in idcs: 
            res.append(l[current_index: index])
            current_index = index

        return res
    
    clients_idcs = [[] for _ in range(n_clients)]
    for cluster_id in range(n_clusters):
        # cluster_split为一个cluster中按照client划分好的样本
        cluster_split = split_list_by_idcs(clusters[cluster_id], clients_counts[cluster_id])

        # 将每一个client的样本累加上去
        for client_id, idcs in enumerate(cluster_split):
            clients_idcs[client_id] += idcs

最后，我们返回每个client对应的样本索引：

    return clients_idcs

接下来我们在EMNIST数据集上调用该函数进行测试，并进行可视化呈现。我们设client数量\(N=10\)，Dirichlet概率分布的参数向量\(\bm{\alpha}\)满足\(\alpha_i=0.4,\space i=1,2,...N\), 混合成分个数为3：

import torch
from torchvision import datasets
import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(42)

if __name__ == "__main__":

    N_CLIENTS = 10
    DIRICHLET_ALPHA = 1
    N_COMPONENTS = 3

    train_data = datasets.EMNIST(root=".", split="byclass", download=True, train=True)
    test_data = datasets.EMNIST(root=".", split="byclass", download=True, train=False)
    n_channels = 1


    input_sz, num_cls = train_data.data[0].shape[0],  len(train_data.classes)


    train_labels = np.array(train_data.targets)

    # 注意每个client不同label的样本数量不同，以此做到Non-IID划分
    client_idcs = mixture_distribution_split_noniid(train_data, num_cls, N_CLIENTS, N_COMPONENTS, DIRICHLET_ALPHA)


    # 展示不同client的不同label的数据分布
    plt.figure(figsize=(20,3))
    plt.hist([train_labels[idc]for idc in client_idcs], stacked=True, 
            bins=np.arange(min(train_labels)-0.5, max(train_labels) + 1.5, 1),
            label=["Client {}".format(i) for i in range(N_CLIENTS)], rwidth=0.5)
    plt.xticks(np.arange(num_cls), train_data.classes)
    plt.legend()
    plt.show()

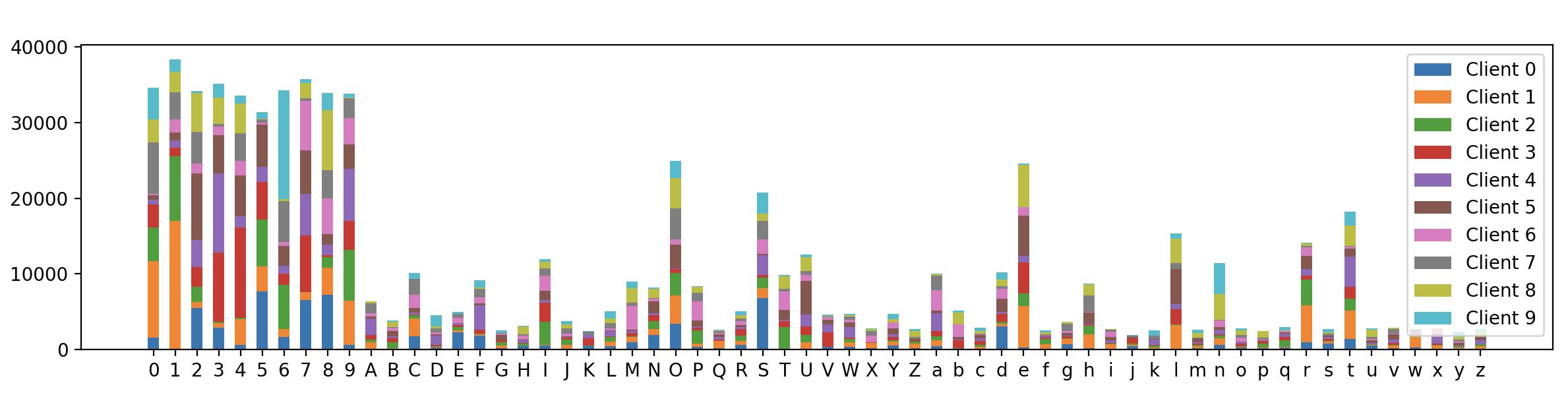
最终的可视化结果如下：

可以看到，62个类别标签在不同client上的分布虽然不同，但相对下面的完全基于Dirichlet的样本划分算法，每个client之间的数据分布显得"更加相似"，即看得出来都来自于一个混合分布，这证明我们的混合分布样本划分算法是有效的。

参考

• [1] McMahan B, Moore E, Ramage D, et al. Communication-efficient learning of deep networks from decentralized data[C]//Artificial intelligence and statistics. PMLR, 2017: 1273-1282.

• [2] Marfoq O, Neglia G, Bellet A, et al. Federated multi-task learning under a mixture of distributions[J]. Advances in Neural Information Processing Systems, 2021, 34.

数学是符号的艺术，音乐是上界的语言。