线性插值和三次样条插值都是非常常用的插值算法，使用插值法，可以帮助我们对离散的样本信息进行扩展，得到样本信息中所不包含的样本点的信息。插值法有着非常广泛的应用场景，就比如某手机厂商所号称的x千万像素拍照，其中插值法就发挥了重要作用。在python的scipy这个库中实现了线性插值算法和三次样条插值算法，而numpy库中实现了线性插值的算法，我们通过这两者的不同使用方式，来看下所得到的插值的结果。
技术背景
插值法在图像处理和信号处理、科学计算等领域中是非常常用的一项技术。不同的插值函数，可以根据给定的数据点构造出来一系列的分段函数。这一点有别于函数拟合，函数拟合一般是指用一个给定形式的连续函数，来使得给定的离散数据点距离函数曲线的总垂直距离最短，不一定会经过所有的函数点。比如在二维坐标系内，用一条直线去拟合一个平面三角形所对应的三个顶点，那么至少有一个顶点是不会落在拟合出来的直线上的。而根据插值法所得到的结果，一定是经过所有给定的离散点的。本文针对scipy和numpy这两个python库的插值算法接口，来看下两者的不同实现方案。
插值算法常用的插值算法比如线性插值，原理非常简单。给定两个点\((X_{t_0},Y_{t_0})\)和\((X_{t_1},Y_{t_1})\)，其中\(t_0<=t_1\)，假如需要计算点\((X_{t_2},Y_{t_2})\)的值，其中\(t_0<=t_2<=t_1\)，那么给定的插值公式就是：
\[\begin{align} X_{t_2}&=(X_{t_1}-X_{t_0})*\frac{t_2-t_0}{t_1-t_0}+X_{t_0}\\ Y_{t_2}&=(Y_{t_1}-Y_{t_0})*\frac{t_2-t_0}{t_1-t_0}+Y_{t_0} \end{align} \]而还有一种比较常用的算法是三次样条插值（cubic spline），其原理是在所有给定的\(n\)个离散点之间构建\(n-1\)个三次函数：
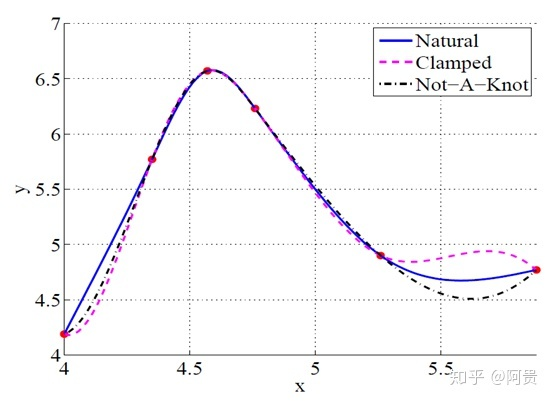
\[y_i=a_i+b_ix_i+c_ix_i^2+d_ix_i^3 \]三次样条插值的约束条件是给定的函数在端点处连续、给定函数的一次导数在端点处连续、给定函数的二次导数在端点处连续，再根据边界条件的不同取法，可以构造出不同的三次样条插值函数。如下图所示就是三种不同的边界条件取法（图片来自于参考链接3）：
接下来看下scipy中的线性插值和三次样条插值的接口调用方式，以及numpy中实现的线性插值的调用方式（numpy中未实现三次样条插值算法）：
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
int1 = interpolate.interp1d(x,y,kind='linear')
int2 = interpolate.interp1d(x,y,kind='cubic')
new_x = np.linspace(0, 4, 30)
plt.figure()
plt.plot(x,y,'o',color='black')
plt.plot(new_x,int1(new_x),'-',color='blue')
plt.plot(new_x,int2(new_x),'--',color='orange')
plt.plot(new_x,np.interp(new_x,x,y),'x',color='red')
plt.legend(['data','linear','cubic','numpy'],loc='best')
plt.savefig('_interpolate.png')
得到的结果如下图所示：
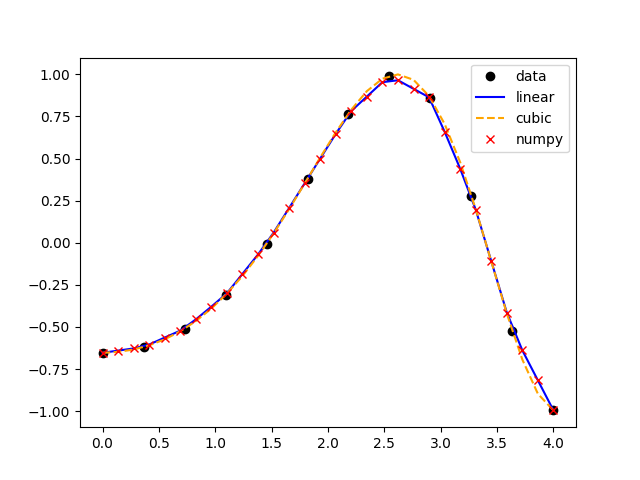
在这个结果中我们发现，numpy的线性插值和scipy的线性插值所得到的结果是一样的，而scipy的三次样条插值的曲线显然要比线性插值更加平滑一些，这也跟三次样条插值算法本身的约束条件有关系。
总结概要线性插值和三次样条插值都是非常常用的插值算法，使用插值法，可以帮助我们对离散的样本信息进行扩展，得到样本信息中所不包含的样本点的信息。插值法有着非常广泛的应用场景，就比如某手机厂商所号称的x千万像素拍照，其中插值法就发挥了重要作用。在python的scipy这个库中实现了线性插值算法和三次样条插值算法，而numpy库中实现了线性插值的算法，我们通过这两者的不同使用方式，来看下所得到的插值的结果。
版权声明本文首发链接为：https://www.cnblogs.com/dechinphy/p/interpolate.html
作者ID：DechinPhy
更多原著文章请参考：https://www.cnblogs.com/dechinphy/
打赏专用链接：https://www.cnblogs.com/dechinphy/gallery/image/379634.html
腾讯云专栏同步：https://cloud.tencent.com/developer/column/91958
参考链接- https://www.yiibai.com/scipy/scipy_interpolate.html
- https://blog.csdn.net/NockinOnHeavensDoor/article/details/83385732
- https://zhuanlan.zhihu.com/p/62860859