D. Alistarh, D. Grubic, J. Li, R. Tomioka, and M. Vojnovic, “QSGD: Communication-Efficient SGD via Gradient Quantization and Encoding,” Advances in Neural Information Processing Systems, vol. 30, 2017, Accessed: Jul. 31, 2021. [Online]. Available: https://proceedings.neurips.cc/paper/2017/hash/6c340f25839e6acdc73414517203f5f0-Abstract.html
作为量化SGD系列三部曲的第二篇,本篇文章是从单机学习到联邦学习的一个重要过渡,在前人的基础上重点进行了理论分析的完善,成为了量化领域绕不开的经典文献。
简介相较于上一篇IBM的文章,本文考虑用梯度量化来改善并行SGD计算中的通信传输问题,并重点研究了通信带宽和收敛时间的关系(precision-variance trade-off)。具体而言,根据information-theoretic lower bounds,当调整每次迭代中传输的比特数时,梯度方差会发生改变,从而进行收敛性分析。实验结果表明在用ResNet-152训练ImageNet时能带来1.8倍的速率提升。
观点- QSGD基于两个算法思想
- 保留原始统计性质的随机量化(来源于量化SGD的实验性质)
- 对量化后梯度的整数部分有损编码(进一步降低比特数)
- 减少通信开销往往会降低收敛速率,因此多训练带来的额外通信次数值不值,是神经网络量化传输需要考虑的重点
- 可以把量化看作一个零均值的噪声,只是它碰巧能够让传输更加有效
- 卷积层比其他层更容易遭受量化带来的性能下降,因此在量化方面,完成视觉任务的网络可能比深度循环网络获益更少
-
方差对于SGD收敛性的影响
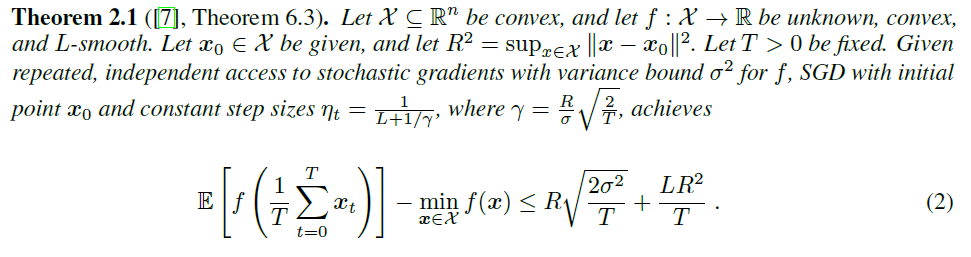
mini-batch操作可以看作是减少方差的一个方法,当第一项主导的时候,由于方差减少到了\(\sigma^2 /m\),因此收敛所需的迭代次数变为\(1/T\)
-
无损的parallel SGD就是一种mini batch,因此将
