 继上一篇文章介绍了分子动力学模拟中常用的LINCS约束算法之后,本文再介绍一种SETTLE约束算法,及其基于Jax的实现方案。LINCS约束算法相对来说比较通用,更适合于成键关系比较复杂的通用的体系,而SETTLE算法更加适用于三原子轴对称体系,比如水分子。SETTLE算法结合velocity-verlet算法,可以确保一个分子只进行整体的旋转运动,互相之间的距离又保持不变。比较关键的是,SETTLE算法所依赖的参数较少,也不需要微分,因此在性能上十分有优势。
技术背景
继上一篇文章介绍了分子动力学模拟中常用的LINCS约束算法之后,本文再介绍一种SETTLE约束算法,及其基于Jax的实现方案。LINCS约束算法相对来说比较通用,更适合于成键关系比较复杂的通用的体系,而SETTLE算法更加适用于三原子轴对称体系,比如水分子。SETTLE算法结合velocity-verlet算法,可以确保一个分子只进行整体的旋转运动,互相之间的距离又保持不变。比较关键的是,SETTLE算法所依赖的参数较少,也不需要微分,因此在性能上十分有优势。
技术背景
在上一篇文章中,我们讨论了在分子动力学里面使用LINCS约束算法及其在具备自动微分能力的Jax框架下的代码实现。约束算法,在分子动力学模拟的过程中时常会使用到,用于固定一些既定的成键关系。例如LINCS算法一般用于固定分子体系中的键长关系,而本文将要提到的SETTLE算法,常用于固定一个构成三角形的体系,最常见的就是水分子体系。对于一个水分子而言,O-H键的键长在模拟的过程中可以固定,H-H的长度,或者我们更常见的作为一个H-O-H的夹角出现的参量,也需要固定。纯粹从计算量来考虑的话,RATTLE约束算法需要迭代计算,LINCS算法需要求矩阵逆(虽然已经给出了截断优化的算法),而SETTLE只涉及到坐标变换,显然SETTLE在约束大规模的水盒子时,性能会更加优秀。
算法流程类似于LINCS算法的,我们先引入一个核心的约束条件:
\[\left|r_{ij}\right|^2-d_{ij}^2=0 \]意思就是说,原子i和原子j之间的距离在分子动力学模拟的迭代过程中保持不变。\(d_{ij}\)可以是初始值,也可以是一个给定值。在满足这个约束条件的同时,其实隐藏着另外一个约束条件:
\[r_{ij}\cdot v_{ij}=0 \]换而言之,如果所有原子的运动方向都与其直接的键连方向垂直,那么在模拟迭代的过程中键长距离就不会发生改变了。
约束前后我们还是需要从一个简单的三角形\(A_0B_0C_0\)模型出发来具体讲解这个算法的流程:

假定三角形\(A_0B_0C_0\)为原始位置,三角形\(A_1B_1C_1\)为没有加约束的坐标更新,而我们的目标是得到三角形\(A_3B_3C_3\)这个加了约束的三角形。这里先解释一下为什么不是三角形\(A_2B_2C_2\)而是三角形\(A_3B_3C_3\),因为这里三角形的变换只是涉及到加了约束条件和没加约束条件的结果,但是实际上加约束条件是一个步骤比较复杂的过程,这里写成三角形\(A_3B_3C_3\)是为了方便跟后续的SETTLE约束所得到的结果下标对齐。
约束算法中的约束条件在上一步的算法过程中,其实我们已经初步的把施加SETTLE约束算法的过程划分成了两个部分:先不加约束的演化,再考虑施加约束的演化。之所以能够这么划分,是因为我们把约束条件考虑成一个约束作用力,这样有两个好处:一是约束力也变成连续可微的参量,二是矢量的作用是可以叠加和拆分的,这里两步的拆分,就是用到了其矢量作用力的效果。

将三角形初始所在的平面定义为\(\pi_0\),在经过未加约束的偏移之后得到了三角形\(A_1B_1C_1\),此时可能已经偏离了原始的平面\(\pi_0\),这里将三个顶点所在的位置都构造一个与\(\pi_0\)相互平行的平面,称为\(\pi_A\)、\(\pi_B\)和\(\pi_C\)。这里可能会有两个需要着重注意的点,第一,我们之所以要定义\(\pi_A\)、\(\pi_B\)和\(\pi_C\)这三个平面,是因为约束力总是在径向的,也就是说,不可能产生与平面\(\pi_0\)相垂直的约束力,因此约束力的作用只是让三个顶点在与\(\pi_0\)平面相平行的平面上运动,也就是这里的\(\pi_A\)、\(\pi_B\)和\(\pi_C\)三个平面。换而言之,三角形\(A_3B_3C_3\)的三个顶点必然在\(\pi_A\)、\(\pi_B\)和\(\pi_C\)三个平面内。第二,因为约束力是分子内部的作用力,也就是对重心的合力为0,不会导致整体分子的漂移,因此,在施加约束力前后,重心的位置不变。如果分别用\(D_1\)和\(D_3\)来标记三角形\(A_1B_1C_1\)和\(A_3B_3C_3\)的重心的话,那么有\(D_1=D_3\)。并且,假如原始位置三角形\(A_0B_0C_0\)的重心\(d_0\)跟\(D_1\)和\(D_3\)如果是在同一个位置的话,那么原始位置的三角形\(A_0B_0C_0\)就可以通过绕重心的旋转跟三角形\(A_3B_3C_3\)重合。
基于\(d_0=D_1=D_3\)的假定,我们可以基于三角形\(A_0B_0C_0\)建立这样一个新的坐标系\(X'Y'Z'\),原点为\(d_0\),\(X'-Y'\)平面与\(\pi_0\)平行,而\(Y'-Z'\)平面过\(A_0\)点:

如果从\(Z'\)轴向\(Z'\)轴负方向看(常规理解就是从上往下看的俯视图),就是这样的一个平面:
 三维旋转
三维旋转
在前面的章节中我们提到,通过旋转操作,可以将初始的坐标旋转到更施加约束之后的坐标完全重合的位置,因此我们先假设三个旋转角,对原始坐标进行旋转操作。最后再根据约束条件来计算对应的旋转角,进而得到施加约束之后的新的坐标,也就是我们最终所需要的结果。在新的坐标系下,我们把三角形\(A_0B_0C_0\)重新标记为三角形\(a_0b_0c_0\),接下来开始对三角形\(a_0b_0c_0\)的一系列三维旋转操作:

在初始条件下,因为三角形跟\(X'-Y'\)处在同一个平面上,因此从\(Y'\)轴向\(Y'\)轴正方向看时,会看到一条直线,此时我们绕\(Y'\)轴旋转一个\(\psi\)的角度,得到了三角形\(a_1b_1c_1\)。

按照同样的操作,绕\(X'\)轴旋转\(\phi\)以及绕\(Z'\)轴旋转\(\theta\)的角度,经过三次的旋转之后,得到一个新的三角形\(a_3b_3c_3\)。而此时的三角形\(a_3b_3c_3\)正是处于跟三角形\(A_3B_3C_3\)完全重合的状态。因此,我们就可以根据约束条件计算出来三个欧拉角\(\psi\)、\(\phi\)和\(\theta\),进而得到我们所需要的约束后的结果:三角形\(A_3B_3C_3\)。
算法解析表达式关于具体解析表达式的推导,可以参考本文末尾的参考文章1中的附录A,这里我们仅展示一些已经推导出来的解析表达式的结果。首先假定未施加约束算法的三角形\(A_1B_1C_1\)在\(X'Y'Z'\)坐标系下的坐标分别为:\([X'_{A_1},Y'_{A_1},Z'_{A_1}]\)、\([X'_{B_1},Y'_{B_1},Z'_{B_1}]\)和\([X'_{C_1},Y'_{C_1},Z'_{C_1}]\),以及三角形\(a_0b_0c_0\)在\(X'Y'Z'\)坐标系下的坐标分别为:
\[\begin{align} a'_0&=[0,r_a,0]\\ b'_0&=[-r_c,-r_b,0]\\ c'_0&=[r_c,-r_b,0] \end{align} \]关于这个坐标数值,再回头看下这个图可能会更加清晰明了一些:

那么我们最终可以得到的旋转角为:
\[\begin{align} \phi&=arcsin\left(\frac{Z'_{A_1}}{r_a}\right)\\ \psi&=arcsin\left(\frac{Z'_{B_1}-Z'_{C_1}}{2r_ccos\phi}\right)\\ \theta&=arcsin\left(\frac{\gamma}{\sqrt{\alpha^2+\beta^2}}\right)-arctan\left(\frac{\beta}{\alpha}\right) \end{align} \]其中\(\alpha\)、\(\beta\)和\(\gamma\)的取值如下:
\[\begin{align} \alpha&=-r_ccos\psi(X'_{B_0}-X'_{C_0})+(-r_bcos\phi-r_csin\psi sin\phi)(Y'_{B_0}-Y'_{A_0})+(-r_bcos\phi+r_csin\psi sin\phi)(Y'_{C_0}-Y'_{A_0})\\ \beta&=-r_ccos\psi(Y'_{C_0}-Y'_{B_0})+(-r_bcos\phi-r_csin\psi sin\phi)(X'_{B_0}-X'_{A_0})+(-r_bcos\phi+r_csin\psi sin\phi)(X'_{C_0}-X'_{A_0})\\ \gamma&=Y'_{B_1}(X'_{B_0}-X'_{A_0})-X'_{B_1}(Y'_{B_0}-Y'_{A_0})+Y'_{C_1}(X'_{C_0}-X'_{A_0})-X'_{C_1}(Y'_{C_0}-Y'_{A_0}) \end{align} \]而最终得到的三角形\(a_3b_3c_3\)的坐标为:
\[\begin{align} a'_3&=\left(-r_acos\phi sin\theta,\ r_acos\phi cos\theta,\ r_asin\phi\right)\\ b'_3&=\left(-r_ccos\psi cos\theta+r_bsin\theta cos\phi+r_csin\theta sin\psi sin\phi,\\ -r_ccos\psi sin\theta-r_bcos\theta cos\phi-r_ccos\theta sin\psi sin\phi,\\ r_csin\psi cos\phi\right)\\ c'_3&=\left(r_ccos\psi cos\theta+r_bsin\theta cos\phi-r_csin\theta sin\psi sin\phi,\\ r_ccos\psi sin\theta-r_bcos\theta cos\phi+r_ccos\theta sin\psi sin\phi,\\ -r_bsin\phi-r_csin\psi cos\phi \right) \end{align} \]在上述的公式中,我们根据未施加约束的三角形\(A_1B_1C_1\)在\(X'Y'Z'\)坐标轴下的新坐标,以及初始的三角形\(a_0b_0c_0\)在\(X'Y'Z'\)坐标轴下的新坐标,就可以计算出\(\phi,\psi,\theta\)这三个空间角。进而可以得到施加约束之后所得到的等效三角形\(a_3b_3c_3\)在\(X'Y'Z'\)坐标轴下的坐标,再经过两个坐标之间的转化之后,就可以得到我们所需要的施加约束条件之后的目标三角形\(A_3B_3C_3\)在原始的\(XYZ\)坐标系下的笛卡尔坐标。
三维空间坐标变换在上一个章节中我们提到了还需要一个三维空间的坐标转化,因为前后采取了两个不同的坐标系。如果分别标记\(R_X,R_Y,R_Z\)为绕着\(X,Y,Z\)轴旋转的矩阵,则相应的旋转矩阵为:
\[R_Y(\psi)=\left( \begin{matrix} cos\psi && 0 && -sin\psi\\ 0 && 1 && 0\\ sin\psi && 0 && cos\psi \end{matrix} \right)\\ R_X(\phi)=\left( \begin{matrix} 1 && 0 && 0\\ 0 && cos\phi && -sin\phi\\ 0 && sin\phi && cos\phi \end{matrix} \right)\\ R_Z(\theta)=\left( \begin{matrix} cos\theta && -sin\theta && 0\\ sin\theta && cos\theta && 0\\ 0 && 0 && 1 \end{matrix} \right) \]我们也可以把这些变换看做是一个整体:\(T(\psi,\phi,\theta)=R_Z(\theta)R_X(\phi)R_Y(\psi)\),这个变换不仅可以用于计算坐标系的变换下所有对应节点的坐标变换,还可以用于计算上一个步骤中提到的三角形\(a_3b_3c_3\)。但是上一个步骤中的三角形\(a_3b_3c_3\)的坐标已经给出,这里我们为了得到坐标系的逆变换,因此不得不把坐标变换的完整形式列出来,则对应的\(T^{-1}(\psi,\phi,\theta)=R_Z(\theta)R_X(\phi)R_Y(\psi)\)就是其逆变换。了解清楚变换的形式之后,我们再回过头来看这个\(XYZ\)坐标系到\(X'Y'Z'\)坐标系的变换:

我们发现这里其实不仅仅是包含有坐标轴的旋转,还包含了坐标系原点的偏移,不过这个漂移倒是比较好处理,可以在后续的计算过程中点出即可。
坐标变换代码实现我们求解从原始的坐标\(XYZ\)到新坐标\(X'Y'Z'\)的代码实现思路是这样的:
- 通过python代码构建一个等腰三角形,通过旋转使得其达到一个初始位置\(A_0B_0C_0\),这个初始位置对应上述章节中的三角形\(A_0B_0C_0\),之所以要通过三个角度的旋转来实现,是为了同时演示这个三维旋转的过程,对应的是如下代码中的
rotation函数; - 计算三角形\(A_0B_0C_0\)的质心
center of mass,表示为\(M\); - 因为三个点就可以固定一个平面,这里我们选取的是\(A\)、\(B\)这两个点以及\(\vec{BC}\otimes \vec{CA}\)这个向量(不能只取三角形所在平面上的点,否则无法正确求解方程,因为对应的参数矩阵秩为2),再假定一个旋转矩阵\(R\),联立一个九元一次方程组,就可以解得旋转矩阵的具体值。

通过这三个点联立的方程组可以表示为:
\[\begin{align} R\left[\left(\begin{matrix} X_{A_0}\\ Y_{A_0}\\ Z_{A_0} \end{matrix}\right)-\vec{M}\right] &=\left(\begin{matrix} 0\\ r_a\\ 0 \end{matrix}\right)\\ R\left[\left(\begin{matrix} X_{B_0}\\ Y_{B_0}\\ Z_{B_0} \end{matrix}\right)-\vec{M}\right] &=\left(\begin{matrix} -r_c\\ -r_b\\ 0 \end{matrix}\right)\\ R\left[\begin{matrix} \vec{BC}\otimes\vec{CA} \end{matrix}\right] &=\left(\begin{matrix} 0\\ 0\\ 1 \end{matrix}\right) \end{align} \]相关的求解代码如下所示:
# settle.py
from jax import numpy as np
from jax import vmap, jit
def rotation(psi,phi,theta,v):
""" Module of rotation in 3 Euler angles. """
RY = np.array([[np.cos(psi),0,-np.sin(psi)],
[0, 1, 0],
[np.sin(psi),0,np.cos(psi)]])
RX = np.array([[1,0,0],
[0,np.cos(phi),-np.sin(phi)],
[0,np.sin(phi),np.cos(phi)]])
RZ = np.array([[np.cos(theta),-np.sin(theta),0],
[np.sin(theta),np.cos(theta),0],
[0,0,1]])
return np.dot(RZ,np.dot(RX,np.dot(RY,v)))
multi_rotation = jit(vmap(rotation,(None,None,None,0)))
if __name__ == '__main__':
import matplotlib.pyplot as plt
# construct params
ra = 0.5
rb = 0.7
rc = 1.2
psi = 0.4
phi = 0.5
theta = 1.3
# construct initial crd
crd = np.array([[0, ra, 0],
[-rc, -rb, 0],
[rc, -rb, 0]])
shift = np.array([0.1, 0.1, 0.1])
crd = multi_rotation(psi,phi,theta,crd) + shift
# get the center of mass
com = np.average(crd,0)
# 3 points are selected to solve the initial rotation matrix
xyz = [0,0,0]
xyz[0] = crd[0]-com
xyz[1] = crd[1]-com
cross = np.cross(crd[2]-crd[1],crd[0]-crd[2])
cross /= np.linalg.norm(cross)
xyz[2] = cross
xyz = np.array(xyz)
inv_xyz = np.linalg.inv(xyz)
v0 = np.array([0,-rc,0])
v1 = np.array([ra,-rb,0])
v2 = np.array([0,0,1])
# final rotation matrix is constructed by following
Rot = np.array([np.dot(inv_xyz,v0),np.dot(inv_xyz,v1),np.dot(inv_xyz,v2)])
print (Rot)
# some test cases and results
origin = crd[0]
print(np.dot(Rot, origin-com))
# [1.4901161e-08 5.0000000e-01 0.0000000e+00]
origin = crd[1]
print(np.dot(Rot, origin-com))
# [-1.2000000e+00 -7.0000005e-01 -5.9604645e-08]
origin = crd[2]
print(np.dot(Rot, origin-com))
# [ 1.2000000e+00 2.0000000e-01 -1.4901161e-08]
origin = xyz[2]
print(np.dot(Rot, origin))
# [0.0000000e+00 2.9802322e-08 1.0000000e+00]
上述代码中所得到的Rot这个矩阵,就是我们所需的将\(XYZ\)坐标系转移到\(X'Y'Z'\)坐标系的旋转矩阵,当然,需要注意的是在做坐标系映射的过程中,除了考虑坐标系的旋转,还需要考虑坐标系的平移,在这里就是重心的偏移量,这个偏移量在原始的文章中是没有使用到的,但是我们实际的模拟过程中是肯定会遇到的。只是说因为约束力的合力是0,因此在从三角形\(A_1B_1C_1\)到三角形\(A_3B_3C_3\)的过程是不需要考虑重心偏移的,但是我们在第一步从三角形\(A_0B_0C_0\)到三角形\(A_1B_1C_1\)或者是三角形\(a_0b_0c_0\)的过程是必然会面临的。同时,在上述代码的结尾处我们给出了四个验证的案例,这与我们所预期的结果是相符合的,坐标值从\(XYZ\)坐标系变换成了以\(\pi_0\)为\(X'-Y'\)平面且\(Y'-Z'\)平面过\(a_0\)点的坐标系上。

需要特别提及的是,上述代码中所使用到的JAX框架支持了vmap这种便捷矢量化计算的操作,因此在rotation函数中只实现了一个旋转矩阵对一个向量的操作,再通过vmap将其扩展到了对多个矢量,也就是多个点空间旋转操作上,变成了multi_rotation函数,这样的操作也更加符合我们对多个原子坐标的定义形式。
在前面的章节中我们已经基本完成了SETTLE约束算法的介绍,这里我们先总结梳理一遍实现SETTLE的步骤,再看下代码实现以及相关的效果:
- 获取\(XYZ\)坐标系下三角形\(A_0B_0C_0\)的坐标以及三角形\(A_1B_1C_1\)的坐标;
- 根据三角形\(A_0B_0C_0\)的坐标计算得\(r_a,r_b,r_c\)的值以及质心\(M\)的坐标;
- 根据三角形\(A_0B_0C_0\)的坐标以及\(r_a,r_b,r_c\)的值和质心\(M\)的坐标,计算\(XYZ\)坐标系到\(X'Y'Z'\)坐标系的变换矩阵\(Rot\)及其逆变换\(Rot^{-1}\);
- 用\(Rot\)和质心坐标计算三角形\(A_1B_1C_1\)在坐标系\(X'Y'Z'\)下的坐标;
- 根据三角形\(A_1B_1C_1\)在坐标系\(X'Y'Z'\)下的坐标计算得三个旋转角\(\phi,\psi,\theta\);
- 根据\(\phi,\psi,\theta\)和\(r_a,r_b,r_c\)计算三角形\(A_3B_3C_3\),也就是我们的目标三角形,在\(X'Y'Z'\)坐标系下的坐标;
- 使用\(Rot^{-1}\)将三角形\(A_3B_3C_3\)在坐标系\(X'Y'Z'\)下的坐标变换回坐标系\(XYZ\)下的坐标,至此就完成了SETTLE算法的实现。
相关代码实现如下所示:
# settle.py
from jax import numpy as np
from jax import vmap, jit
def rotation(psi,phi,theta,v):
""" Module of rotation in 3 Euler angles. """
RY = np.array([[np.cos(psi),0,-np.sin(psi)],
[0, 1, 0],
[np.sin(psi),0,np.cos(psi)]])
RX = np.array([[1,0,0],
[0,np.cos(phi),-np.sin(phi)],
[0,np.sin(phi),np.cos(phi)]])
RZ = np.array([[np.cos(theta),-np.sin(theta),0],
[np.sin(theta),np.cos(theta),0],
[0,0,1]])
return np.dot(RZ,np.dot(RX,np.dot(RY,v)))
multi_rotation = jit(vmap(rotation,(None,None,None,0)))
def get_rot(crd):
""" Get the coordinates transform matrix. """
# get the center of mass
com = np.average(crd, 0)
rc = np.linalg.norm(crd[2]-crd[1])/2
ra = np.linalg.norm(crd[0]-com)
rb = np.sqrt(np.linalg.norm(crd[2]-crd[0])**2-rc**2)-ra
# 3 points are selected to solve the initial rotation matrix
xyz = [0, 0, 0]
xyz[0] = crd[0] - com
xyz[1] = crd[1] - com
cross = np.cross(crd[2] - crd[1], crd[0] - crd[2])
cross /= np.linalg.norm(cross)
xyz[2] = cross
xyz = np.array(xyz)
inv_xyz = np.linalg.inv(xyz)
v0 = np.array([0, -rc, 0])
v1 = np.array([ra, -rb, 0])
v2 = np.array([0, 0, 1])
# final rotation matrix is constructed by following
Rot = np.array([np.dot(inv_xyz, v0), np.dot(inv_xyz, v1), np.dot(inv_xyz, v2)])
inv_Rot = np.linalg.inv(Rot)
return Rot, inv_Rot
def xyzto(Rot, crd, com):
""" Apply the coordinates transform matrix. """
return np.dot(Rot, crd-com)
multi_xyzto = jit(vmap(xyzto,(None,0,None)))
def toxyz(Rot, crd, com):
""" Apply the inverse of transform matrix. """
return np.dot(Rot, crd-com)
multi_toxyz = jit(vmap(toxyz,(None,0,None)))
def get_circumference(crd):
""" Get the circumference of all triangles. """
return np.linalg.norm(crd[0]-crd[1])+np.linalg.norm(crd[0]-crd[2])+np.linalg.norm(crd[1]-crd[2])
jit_get_circumference = jit(get_circumference)
def get_angles(crd_0, crd_t0, crd_t1):
""" Get the rotation angle psi, phi and theta. """
com = np.average(crd_0, 0)
rc = np.linalg.norm(crd_0[2] - crd_0[1]) / 2
ra = np.linalg.norm(crd_0[0] - com)
rb = np.sqrt(np.linalg.norm(crd_0[2] - crd_0[0]) ** 2 - rc ** 2) - ra
phi = np.arcsin(crd_t1[0][2]/ra)
psi = np.arcsin((crd_t1[1][2]-crd_t1[2][2])/2/rc/np.cos(phi))
alpha = -rc*np.cos(psi)*(crd_t0[1][0]-crd_t0[2][0])+(-rb*np.cos(phi)-rc*np.sin(psi)*np.sin(phi))*(crd_t0[1][1]-crd_t0[0][1])+ \
(-rb*np.cos(phi)+rc*np.sin(psi)*np.sin(phi))*(crd_t0[2][1]-crd_t0[0][1])
beta = -rc*np.cos(psi)*(crd_t0[2][1]-crd_t0[1][1])+(-rb*np.cos(phi)-rc*np.sin(psi)*np.sin(phi))*(crd_t0[1][0]-crd_t0[0][0])+ \
(-rb*np.cos(phi)+rc*np.sin(psi)*np.sin(phi))*(crd_t0[2][0]-crd_t0[0][0])
gamma = crd_t1[1][1]*(crd_t0[1][0]-crd_t0[0][0])-crd_t1[1][0]*(crd_t0[1][1]-crd_t0[0][1])+\
crd_t1[2][1]*(crd_t0[2][0]-crd_t0[0][0])-crd_t1[2][0]*(crd_t0[2][1]-crd_t0[0][1])
sin_part = gamma/np.sqrt(alpha**2+beta**2)
theta = np.arcsin(sin_part)-np.arctan(beta/alpha)
return phi, psi, theta
jit_get_angles = jit(get_angles)
def get_d3(crd_0, psi, phi, theta):
""" Calculate the new coordinates by 3 given angles. """
com = np.average(crd_0, 0)
rc = np.linalg.norm(crd_0[2] - crd_0[1]) / 2
ra = np.linalg.norm(crd_0[0] - com)
rb = np.sqrt(np.linalg.norm(crd_0[2] - crd_0[0]) ** 2 - rc ** 2) - ra
return np.array([[-ra*np.cos(phi)*np.sin(theta), ra*np.cos(phi)*np.cos(theta), ra*np.sin(phi)],
[-rc*np.cos(psi)*np.cos(theta)+rb*np.sin(theta)*np.cos(phi)+rc*np.sin(theta)*np.sin(psi)*np.sin(phi),
-rc*np.cos(psi)*np.sin(theta)-rb*np.cos(theta)*np.cos(phi)-rc*np.cos(theta)*np.sin(psi)*np.sin(phi),
-rb*np.sin(phi)+rc*np.sin(psi)*np.cos(phi)],
[rc*np.cos(psi)*np.cos(theta)+rb*np.sin(theta)*np.cos(phi)-rc*np.sin(theta)*np.sin(psi)*np.sin(phi),
rc*np.cos(psi)*np.sin(theta)-rb*np.cos(theta)*np.cos(phi)+rc*np.cos(theta)*np.sin(psi)*np.sin(phi),
-rb*np.sin(phi)-rc*np.sin(psi)*np.cos(phi)]])
jit_get_d3 = jit(get_d3)
if __name__ == '__main__':
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as onp
onp.random.seed(0)
# construct params
ra = 1.0
rb = 0.5
rc = 1.2
psi = 0.4
phi = 0.5
theta = 1.3
# construct initial crd
crd = np.array([[0, ra, 0],
[-rc, -rb, 0],
[rc, -rb, 0]])
shift = np.array([0.1, 0.1, 0.1])
# get the initial crd
crd_0 = multi_rotation(psi,phi,theta,crd) + shift
vel = np.array(onp.random.random(crd_0.shape)-0.5)
dt = 1
# get the unconstraint crd
crd_1 = crd_0 + vel * dt
com_0 = np.average(crd_0, 0)
com_1 = np.average(crd_1, 0)
# get the coordinate transform matrix and correspond inverse operation
rot, inv_rot = get_rot(crd_0)
crd_t0 = multi_xyzto(rot, crd_0, com_0)
com_t0 = np.average(crd_t0, 0)
crd_t1 = multi_xyzto(rot, crd_1, com_1)+com_1
com_t1 = np.average(crd_t1, 0)
print ('crd_t1:\n', crd_t1)
# crd_t1:
# [[0.11285806 1.1888411 0.22201033]
# [-1.3182535 - 0.35559598 0.3994387]
# [1.5366794 - 0.00262779
# 0.3908713]]
phi, psi, theta = jit_get_angles(crd_0, crd_t0, crd_t1-com_t1)
crd_t3 = jit_get_d3(crd_t0,psi,phi,theta)+com_t1
com_t3 = np.average(crd_t3, 0)
crd_3 = multi_toxyz(inv_rot, crd_t3, com_t3) + com_1
print ('crd_t3:\n', crd_t3)
# crd_t3:
# [[0.01470824 1.2655654 0.22201033]
# [-1.0361676 - 0.3326143 0.39943868]
# [1.3527434 - 0.10233352
# 0.39087126]]
print(jit_get_circumference(crd_0))
# 6.2418747
print(jit_get_circumference(crd_t0))
# 6.2418737
print(jit_get_circumference(crd_1))
# 6.853938
print(jit_get_circumference(crd_t1))
# 6.8539376
print(jit_get_circumference(crd_t3))
# 6.2418737
print(jit_get_circumference(crd_3))
# 6.241874
# Plotting
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x_0 = np.append(crd_0[:,0],crd_0[0][0])
y_0 = np.append(crd_0[:,1],crd_0[0][1])
z_0 = np.append(crd_0[:,2],crd_0[0][2])
ax.plot(x_0, y_0, z_0, color='black')
x_1 = np.append(crd_1[:, 0], crd_1[0][0])
y_1 = np.append(crd_1[:, 1], crd_1[0][1])
z_1 = np.append(crd_1[:, 2], crd_1[0][2])
ax.plot(x_1, y_1, z_1, color='blue')
x_3 = np.append(crd_3[:, 0], crd_3[0][0])
y_3 = np.append(crd_3[:, 1], crd_3[0][1])
z_3 = np.append(crd_3[:, 2], crd_3[0][2])
ax.plot(x_3, y_3, z_3, color='red')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
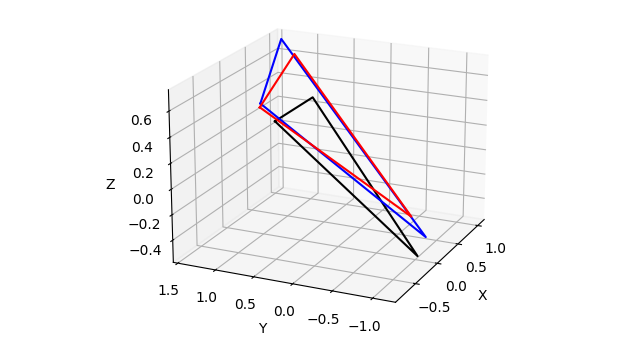
这个代码实现的流程,可以通过理解main函数中的顺序来进行解读:首先用随机数构建前后两个三角形\(A_0B_0C_0\)和\(A_1B_1C_1\)用于测试SETTLE算法。然后使用get_rot函数来得到从坐标\(XYZ\)到\(X'Y'Z'\)的映射旋转关系。但是这里需要注意的是,这个函数得到的旋转矩阵只有旋转给定矢量的功能,其中重心偏移是需要自己手动加上的。有了这一层的映射关系关系之后,就可以计算得到\(X'Y'Z'\)坐标系下所对应的两个三角形,在代码中就是crd_t0和crd_t1。根据新坐标系下的两个三角形的坐标,可以计算出来\(\psi,\phi,\theta\)这三个角度,进而计算出来我们所需要的\(X'Y'Z'\)坐标系下的三角形\(a_3b_3c_3\),也就是代码中的crd_t3。此时我们通过计算所得到的三角形的周长,我们可以发现中间未加约束的周长变化较大,但是再施加约束之后,周长与原始三角形的周长一致。在最后,我画了几个三维图以供示意:

其中黑色的是原始的三角形,蓝色的是未施加约束条件的偏移,其中重心也发生了较为明显的变化,而红色的三角形对应的是施加约束后的三角形。还可以从另外一个角度来查看施加约束前后的两个三角形的平面关系:

需要特别注意的是,获取坐标变换的矩阵只能针对矢量进行旋转,也就是这里针对重心的旋转。而从未施加约束的三角形\(A_1B_1C_1\)到施加约束的三角形\(A_3B_3C_3\)重心是不会发生改变的,因此在施加\(Rot^{-1}\)的时候,最后需要加上三角形\(A_1B_1C_1\)在\(XYZ\)坐标轴下的重心,才是三角形\(a_3b_3c_3\)在\(XYZ\)坐标轴下的真正位置。
速度更新公式当SETTLE应用在分子模拟当中的时候,不仅仅是更新约束前后的位置,相对应的,速度也需要更新。这里我们没有将其实现到代码当中,仅仅放一下公式,以供参考:

然后将\(\tau_{AB},\tau_{BC},\tau_{CA}\)的值代入到如下的公式:

就可以得到更新后的速度。相关内容并不是很复杂,读者可以自行实现。
总结概要继上一篇文章介绍了分子动力学模拟中常用的LINCS约束算法之后,本文再介绍一种SETTLE约束算法,及其基于Jax的实现方案。LINCS约束算法相对来说比较通用,更适合于成键关系比较复杂的通用的体系,而SETTLE算法更加适用于三原子轴对称体系,比如水分子。SETTLE算法结合velocity-verlet算法,可以确保一个分子只进行整体的旋转运动,互相之间的距离又保持不变。比较关键的是,SETTLE算法所依赖的参数较少,也不需要微分,因此在性能上十分有优势。
版权声明本文首发链接为:https://www.cnblogs.com/dechinphy/p/settle.html
作者ID:DechinPhy
更多原著文章请参考:https://www.cnblogs.com/dechinphy/
打赏专用链接:https://www.cnblogs.com/dechinphy/gallery/image/379634.html
腾讯云专栏同步:https://cloud.tencent.com/developer/column/91958
参考文章- SETTLE: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. Shuichi Miyamoto and Peter A.Kollman.
*注:本文所有的算法流程示意图,均来自于参考文章1
“留一手”加剧内卷,“讲不清”浪费时间。