上一章我们介绍了级联阴影贴图。刚开始的时候我尝试了给CSM直接加上PCSS,但不管怎么调难以达到说得过去的效果。然后文章越翻越觉得阴影就是一个巨大的坑,考虑到时间关系,本章只实现了方差阴影贴图(VSM)、指数阴影贴图(ESM)和指数方差阴影贴图(EVSM)作为引子,然后将相关扩展放在文末。
现在假定读者已经读过下面的内容:
DirectX11 With Windows SDK完整目录
欢迎加入QQ群: 727623616 可以一起探讨DX11,以及有什么问题也可以在这里汇报。
Variance Shadow Map关于Shadow Mapping,我们可以将比较深度的过程用这样一个函数表示:\(H(d_o-d_r)\)。其中\(d_r\)是receiver的深度,\(d_o\)是occluder的深度。很明显,当\(d_o-d_r<0\)时,\(H(d_o-d_r)=0\);\(d_o-d_r\geq0\)时,\(H(d_o-d_r)=1\)。
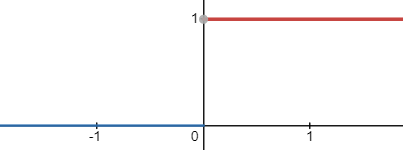
将该函数拆分成occluder项和receiver项,有利于我们对occluder项使用图片空间的模糊或者硬件mipmap进行pre-filter处理以用于软阴影。并且由于我们将要改变阴影测试的方法,就不再需要为了缓解shadow acne(阴影粉刺)而使用Depth bias。
受到Deep Shadow Maps的启发,可以使用概率表示的方式。给定当前receiver的深度值,occluder的深度值现在表示为一个随机变量:
\[f(d_r)=P(d_o\geq d_r) \]上式变成了一个概率分布函数,判断当前像素位于阴影之外的概率。
假设occluder近似满足单峰分布,那么它可以由均值和方差表示。这两者可通过一阶矩(moment)和二阶矩所派生:
\[\mu=E(d_o)\\ \sigma^2=E(d_o^2)-E(d_o)^2 \]其中一阶矩和二阶矩由下面的公式计算:
\[E(x)=\int xp(x)dx\\ E(x^2)=\int x^2p(x)dx \]本质上就是对shadow map做一个滤波(如盒型滤波或高斯滤波等):
\[E(d_o)\approx\sum w_i d_i\\ E(d_o^2)\approx\sum w_i d_i^2 \]在算出均值和方差后,紧接着我们就可以根据切比雪夫不等式来找出\(P(d_o\geq d_r)\)的上界:
\[P(d_o\geq d_r)\leq p_{max}(d_r)\equiv \frac{\sigma^2}{\sigma^2+(\mu-d_r)^2} \]当\(\sigma^2=0, \mu=d_r\)时,上式未定义,为此可以在分子分母同时加上一个极小量\(\epsilon\),或者是\(\sigma^2<\epsilon\)时直接让\(\sigma^2:=\epsilon\)。此时没有遮蔽的话值为1; 产生遮蔽的话值接近0。
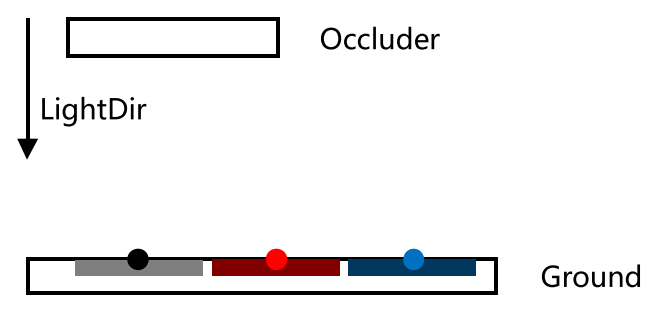
看上图,黑点所属的区域完全被Occluder遮蔽,因此\(\sigma^2=0, \mu < d_r, p_{max}(d_r)\approx 0\)
红点所属的区域部分被Occluder遮蔽,有\(\sigma^2>0, \mu < d_r\),且红点越往右靠,\(p_{max}(d_r)\)越接近1
蓝点所属的区域没有遮蔽,因此\(\sigma^2=0, \mu = d_r, p_{max}(d_r)=1\)
根据上式我们可以写出如下HLSL代码:
float ChebyshevUpperBound(float2 moments,
float receiverDepth,
float minVariance,
float lightBleedingReduction)
{
float variance = moments.y - (moments.x * moments.x);
variance = max(variance, minVariance); // 防止0除
float d = receiverDepth - moments.x;
float p_max = variance / (variance + d * d);
// 单边切比雪夫
return (receiverDepth <= moments.x ? 1.0f : p_max);
}
而为了能够获得\(d_o\)和\(d_o^2\),显然我们不能靠深度图来缓存,而需要额外的R32G32_FLOAT纹理来记录。如果只是单纯为了记录\(d_o\)和\(d_o^2\),可以在绘制深度图的同时将\(d_o\)和\(d_o^2\)写入到RTV上。
而由于我们最终要使用的是\(E(d_o)\)和\(E(d_o^2)\),我们可以对其进行一个pre-filter的处理,具体包括:
- 使用MSAA记录更多深度
- 使用盒型滤波或高斯滤波处理方差阴影贴图
- 使用mipmap
而采样的时候我们可以对方差阴影贴图使用各种方式,比如点采样、线性采样、各向异性采样。
下面的代码将方差阴影写入级联:
// Shadow.hlsl
Texture2D g_TextureShadow : register(t0);
float2 VarianceShadowPS(float4 posH : SV_Position,
float2 texCoord : TEXCOORD) : SV_Target
{
uint2 coords = uint2(posH.xy);
float2 depth;
depth.x = g_TextureShadow[coords];
depth.y = depth.x * depth.x;
return depth;
}
为了更近一步考虑周围像素的深度,可以使用屏幕空间滤波获得\(E(d_o)\)和\(E(d_o^2)\),使用盒型滤波或高斯滤波都可以:
// Shadow.hlsl
#ifndef BLUR_KERNEL_SIZE
#define BLUR_KERNEL_SIZE 3
#endif
static const int BLUR_KERNEL_BEGIN = BLUR_KERNEL_SIZE / -2;
static const int BLUR_KERNEL_END = BLUR_KERNEL_SIZE / 2 + 1;
static const float FLOAT_BLUR_KERNEL_SIZE = (float)BLUR_KERNEL_SIZE;
Texture2D g_TextureShadow : register(t1); // 用于模糊
SamplerState g_SamplerPointClamp : register(s0);
float2 VSMHorizontialBlurPS(float4 posH : SV_Position,
float2 texcoord : TEXCOORD) : SV_Target
{
float2 depths = 0.0f;
[unroll]
for (int x = BLUR_KERNEL_BEGIN; x < BLUR_KERNEL_END; ++x)
{
depths += g_TextureShadow.Sample(g_SamplerPointClamp, texcoord, int2(x, 0));
}
depths /= FLOAT_BLUR_KERNEL_SIZE;
return depths;
}
float2 VSMVerticalBlurPS(float4 posH : SV_Position,
float2 texcoord : TEXCOORD) : SV_Target
{
float2 depths = 0.0f;
[unroll]
for (int y = BLUR_KERNEL_BEGIN; y < BLUR_KERNEL_END; ++y)
{
depths += g_TextureShadow.Sample(g_SamplerPointClamp, texcoord, int2(0, y));
}
depths /= FLOAT_BLUR_KERNEL_SIZE;
return depths;
}
其中Sample的可选第三个参数offset用来控制采样行为,往x方向和y方向偏移多少个像素单位,其范围只能在[-8, 7],超过这个范围编译就会报错。你也可以不使用offset,改为额外提供宽高信息来求texel的uv offset。
最后在绘制完所有级联的方差阴影贴图后,我们可以选择是否使用GenerateMips。
VSM最大的问题在于漏光现象,见下图(不得不说这漏光是真的严重)。

虽然切比雪夫不等式给了一个\(P(x\geq t)\)的上界,但并没保证对这个上界有较好的近似。考虑下图的情况:
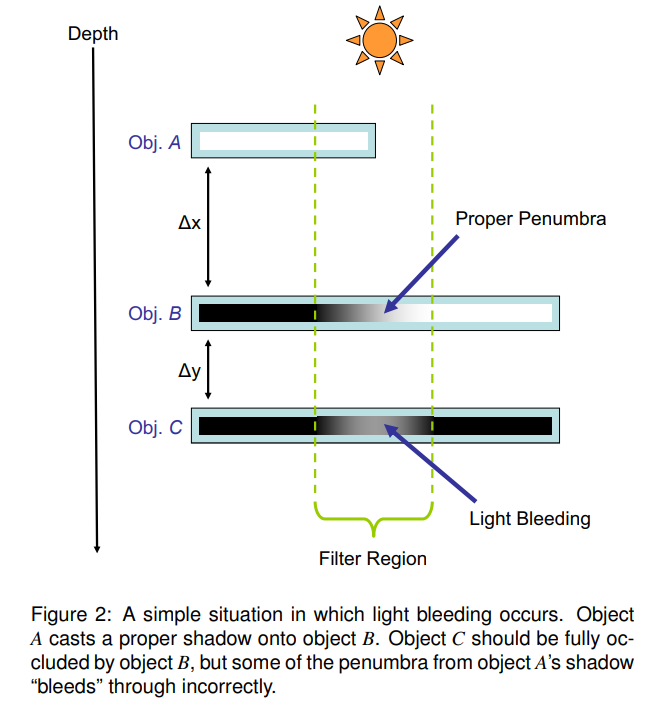
让这三个物体从上到下标记为A、B、C,对应的深度值为a、b、c。只有物体A和B处于滤波区域,C则作为receiver被两个物体挡住本应是看不到光源的。我们假定当前着色点位于C中滤波区域的中心我们可以得到下面两个矩:
\[M_1=\frac{a+b}{2}\\ M_2=\frac{a^2+b^2}{2} \]然后我们可以算出均值和方差:
\[\mu=\frac{a+b}{2}\\ \sigma^2=M_2^2-(M_1)^2=\frac{(a-b)^2}{4} \]上图中有\(\Delta{x}=b-a\)和\(\Delta{y}=c-b\),因此可视性函数有:
\[\begin{aligned} p(\Delta{y})&=\frac{\frac{1}{4}\Delta{x^2}}{\frac{1}{4}\Delta{x^2}+(\Delta{y}+\frac{1}{2}\Delta{x})^2}\\ &=\frac{1}{2+4\frac{\Delta{y}}{\Delta{x}}+4(\frac{\Delta{y}}{\Delta{x}})^2} \end{aligned} \]下图是\(\frac{\Delta{y}}{\Delta{x}}\)与\(p(\Delta{y})\)的函数关系图像。如果\(\frac{\Delta{y}}{\Delta{x}}\)很小的话,会导致\(p(\Delta{y})\)逐渐向0.5靠拢,从而导致了漏光现象的出现。
对于复杂的场景来说,仅调整光线方向并不能解决问题,不得不吐槽发电厂这个模型简直就是各路算法的埋葬场。
但如果我们尝试增加更多采样来解决这个问题,那又会牺牲效率,那还不如使用PCF。因为使用VSM等基于概率的阴影算法是相比于传统PCF的效率较高,当然代价是在极端情况下带来的物理不准确性。
减少漏光的近似算法如果receiver的深度值为\(z\),且它被某个滤波区域完全阻挡,那么有\(d_o-d_r<0, (z-d)^2>0, p_{max}<1\),即该表面永远接受不到满光照的强度
我们可以修改\(p_{max}\)的值,让其在低于某个\(amount\in[0, 1]\)值的时候直接归零,然后将\([amount,1]\)重新映射到\([0,1]\):
float Linstep(float a, float b, float v)
{
return saturate((v - a) / (b - a));
}
// 令[0, amount]的部分归零并将(amount, 1]重新映射到(0, 1]
float ReduceLightBleeding(float pMax, float amount)
{
return Linstep(amount, 1.0f, pMax);
}
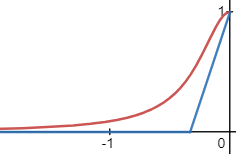
当然,我们也可以向VarianceShadows11的例子中,对\(p_{max}\)套上一个幂指数,然后通过这个幂指数来控制漏光。
现在求\(p_{max}\)的方法变成了:
float ChebyshevUpperBound(float2 moments,
float receiverDepth,
float minVariance,
float lightBleedingReduction)
{
float variance = moments.y - (moments.x * moments.x);
variance = max(variance, minVariance); // 防止0除
float d = receiverDepth - moments.x;
float p_max = variance / (variance + d * d);
p_max = ReduceLightBleeding(p_max, lightBleedingReduction);
// 单边切比雪夫
return (receiverDepth <= moments.x ? 1.0f : p_max);
}
在使用梯度采样级联阴影时,可能会在两个级联的边界区域出现下图所示的问题。


使用各项异性滤波由于动态流控制导致在级联之间出现的接缝
采样指令使用像素之间的导数来计算mipmap等级,也被各项异性过滤所需。这可能会在各项异性过滤或mipmap选择的时候引发问题。当2x2像素块在像素着色器中使用不同的分支时,GPU硬件计算出的导数是不合理的。这会导致在级联边缘出现跳变。
该问题可以通过计算光照空间下位置的偏导来解决;光照空间的坐标并没有指定所选的级联。计算出的导数可以变换到对应级联所属的投影纹理空间,从而可以求出正确的mipmap等级或被各项异性过滤使用:
float CalculateVarianceShadow(float4 shadowTexCoord,
float4 shadowTexCoordViewSpace,
int currentCascadeIndex)
{
float percentLit = 0.0f;
float2 moments = 0.0f;
// 为了将求导从动态流控制中拉出来,我们计算观察空间坐标的偏导
// 从而得到投影纹理空间坐标的偏导
float3 shadowTexCoordDDX = ddx(shadowTexCoordViewSpace).xyz;
float3 shadowTexCoordDDY = ddy(shadowTexCoordViewSpace).xyz;
shadowTexCoordDDX *= g_CascadeScale[currentCascadeIndex].xyz;
shadowTexCoordDDY *= g_CascadeScale[currentCascadeIndex].xyz;
moments += g_TextureShadow.SampleGrad(g_SamplerShadow,
float3(shadowTexCoord.xy, (float) currentCascadeIndex),
shadowTexCoordDDX.xy, shadowTexCoordDDY.xy).xy;
percentLit = ChebyshevUpperBound(moments, shadowTexCoord.z, 0.00001f, g_LightBleedingReduction);
return percentLit;
}
VSM具有如下优点:
- 可以使用图片空间blur或硬件filtering来产生软阴影
- 不需要处理shadow acne问题,因此也不需要引入depth bias
但它也有如下缺点:
- 需要原来深度图占用显存空间的两倍来存放\(d_o\)和\(d_o^2\)
- 在具有高方差分布的区域容易产生漏光(Light Bleeding)
- 大卷积核滤波会使漏光现象更加严重(因为方差值变大了)
我们可以注意到,指数函数能够用来近似step函数。指数阴影贴图的核心公式如下:
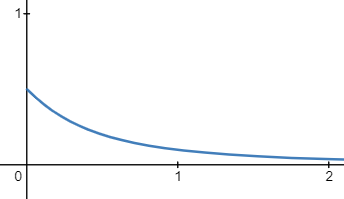
\[f(z)=e^{c(d-z)}, d<z, c>0f(z)=e^{c(d-z)}, d<z, c>0 \]在固定\(c\)的情况下,随着occluder逐渐远离receiver,\(d-z\)从0向负数变动,对应的函数图像如下:
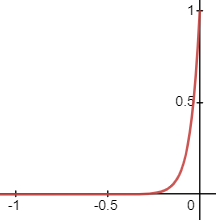
为此我们可以将上式拆分成\(e^{cd}\)和\(e^{-cz}\)项。深度图负责前面一项,receiver可以得到后一项。
这种表示的好处在于简单,并且和VSM一样,可以对\(e^{cd}\)项进行blur,并且没有shadow acne的问题。而相比于VSM,它只需要存一项就可以用。
上图中的\(c=20\),可以看出,如果\(d\)和\(z\)比较接近的话仍然会出现比较严重的漏光,为此需要让c的值变得更大。下图是\(c=100\)的效果:
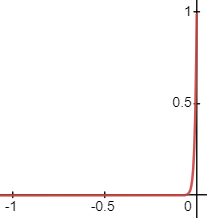
但深度图直接保存\(e^{cd}\)的话会面临一个严重的问题:浮点数的表示范围是有限的,到\(e^{88}\)的时候就已经接近浮点表示的上界了,\(c\)值过大则无法表示左边部分的范围。而为了能够产生跟一开始那张函数图接近跳变的效果,需要让c能够表示得更大,否则在\(d-z\)逼近0的时候误差会很大。
提升精度前面提到如果\(c\)太大,\(e^{cd}\)可能会超过float的表示上界,但\(c(d-z)\)本身远小于\(cd\),不容易越界。在不需要blur的情况下只需要在shadow map生成的时候保存d或者cd即可。
但可以blur也是ESM的优点之一,为此我们需要在blur的部分进行改进。在Lighting Research at Bungie中,提到了一种指数空间滤波的方式。首先对N个样本的加权求和有:
\[\begin{aligned}\sum_{i=0}^N w_i e^{cd_{o_i}}&= e^{cd_{o_0}}(w_0+\sum_{i=1}^Nw_i e^{c(d_{o_i}-d_{o_0})})\\ &=e^{cd_{o_0}}\cdot e^{ln(w_0+\sum_{i=1}^Nw_i e^{c(d_{o_i}-d_{o_0})})}\\ &=e^{cd_{o_0} + ln(w_0+\sum_{i=1}^Nw_i e^{c(d_{o_i}-d_{o_0})})} \end{aligned} \]即我们只需要在blur的时候求出即可:
\[cd_{o_0} + ln(w_0+\sum_{i=1}^Nw_i e^{c(d_{o_i}-d_{o_0})}) \]HLSL代码指数阴影贴图相关的HLSL代码如下:
float ESMLogGaussianBlurPS(float4 posH : SV_Position,
float2 texcoord : TEXCOORD) : SV_Target
{
float cd0 = g_TextureShadow.Sample(g_SamplerPointClamp, texcoord);
float sum = g_BlurWeights[FLOAT_BLUR_KERNEL_SIZE / 2] * g_BlurWeights[FLOAT_BLUR_KERNEL_SIZE / 2];
[unroll]
for (int i = BLUR_KERNEL_BEGIN; i < BLUR_KERNEL_END; ++i)
{
for (int j = BLUR_KERNEL_BEGIN; j < BLUR_KERNEL_END; ++j)
{
float cdk = g_TextureShadow.Sample(g_SamplerPointClamp, texcoord, int2(i, j)) * (float) (i != 0 || j != 0);
sum += g_BlurWeights[i - BLUR_KERNEL_BEGIN] * g_BlurWeights[j - BLUR_KERNEL_BEGIN] * exp(cdk - cd0);
}
}
sum = log(sum) + cd0;
sum = isinf(sum) ? 84.0f : sum; // 防止溢出
return sum;
}
//--------------------------------------------------------------------------------------
// ESM:采样深度图并返回着色百分比
//--------------------------------------------------------------------------------------
float CalculateExponentialShadow(float4 shadowTexCoord,
float4 shadowTexCoordViewSpace,
int currentCascadeIndex)
{
float percentLit = 0.0f;
float occluder = 0.0f;
float3 shadowTexCoordDDX = ddx(shadowTexCoordViewSpace).xyz;
float3 shadowTexCoordDDY = ddy(shadowTexCoordViewSpace).xyz;
shadowTexCoordDDX *= g_CascadeScale[currentCascadeIndex].xyz;
shadowTexCoordDDY *= g_CascadeScale[currentCascadeIndex].xyz;
occluder += g_TextureShadow.SampleGrad(g_SamplerShadow,
float3(shadowTexCoord.xy, (float) currentCascadeIndex),
shadowTexCoordDDX.xy, shadowTexCoordDDY.xy).x;
percentLit = saturate(exp(occluder - g_MagicPower * shadowTexCoord.z));
return percentLit;
}
这样就把receiver和occluder之间深度的矛盾,转移到了occluder与相邻occluder之间深度的矛盾了。但如果滤波时,相邻occluder之间的深度差很大,或者receiver位于非平面区域,会导致当前occluder失去软阴影效果,并退变成类似锯齿的效果,即便我们使用了滤波操作。这部分问题可以通过降低c值解决,让指数函数以一个较低的速率增长,从而降低滤波区域的跳变程度:



而当\(c(d-z)\rightarrow 0\)时,\(e^{c(d-z)}\rightarrow 1\)。靠近遮挡物的地方会有不可避免的漏光。

由于深度值已经位于线性空间,那么c值一定会有一个随深度差最大值变化的上界。这时候更多需要依赖于手工调整。
优缺点总结ESM具有如下优点:
- 可以使用图片空间blur或硬件filtering来产生软阴影,也不需要开很大的Blur
- 不需要处理shadow acne问题,因此也不需要引入depth bias
- 相比VSM只需要用1个float
但它也有如下缺点:
- 为了提升精度需要用特定的Blur,在blur的过程会牺牲一定效率
- 邻近像素深度变化较大或位于非平面区域的话blur可能会失效
- 近处漏光问题
正如前面所说的,漏光现象在\(\Delta{y}\)和\(\Delta{x}\)的比值非常小的时候会特别明显。我们可以考虑使用一些对x和y的wrap来尝试提升\(\Delta{y}\)和\(\Delta{x}\)的比值。
例如我们可以使用上面\(e^{cx}\)的wrapper,这里c是一个正数。然后对\(e^{cx}\)求均值和方差,然后使用切比雪夫不等式求\(p_{max}\)。
这样原来\(\Delta{y}/\Delta{x}\)就变成了\(e^{\Delta{y}-\Delta{x}}\)。
在前面Variance Shadow Map提到的漏光情况下,我们用红色直线表示\(p(\Delta{y})\)关于\(\Delta{y}/\Delta{x}\)的函数关系式,蓝色直线表示\(p(e^{\Delta{y}})\)关于\(\Delta{y}/\Delta{x}\)的函数关系式
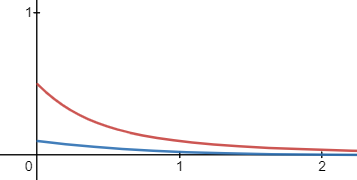
可以看到,经过\(e^{cx}\)的wrapper后,可以有效抑制,c只要增大一些就可以将整段蓝色曲线继续压低(除了左端点不变)。
但是随着c的增大,远处场景的阴影反而出现了问题

这时候我们可以再使用另外一个wrapper:\(-e^{-cx}\)。这时候receiver和occluder的身份就像是调换了一样,以非平面区域B的视角看C就像是平面区域,使得B的阴影区域变平滑了(就像它们在C上那样),从而避免了ESM的非平面问题。
这两个wrap一起使用时,对应样例程序中的EVSM4,否则为EVSM2。为了方便观察,我们对EVSM4的c项分开为一个作用在正指数的\(c_{pos}\)和作用在负指数的\(c_{neg}\)。由于\(e^{cx}\)和\(-e^{-cx}\)都是单调递增函数,这两个wrapper都可以使用切比雪夫不等式,最后取两个上限概率之中的最小值即可。这时候artifacts仅在VSM和ESM会同时出现的地方产生,而增加c值可以减缓这些问题。
HLSL代码EVSM的HLSL代码如下:
float2 GetEVSMExponents(in float positiveExponent, in float negativeExponent, in int is16BitFormat)
{
const float maxExponent = (is16BitFormat ? 5.54f : 42.0f);
float2 exponents = float2(positiveExponent, negativeExponent);
// 限制指数范围防止出现溢出
return min(exponents, maxExponent);
}
// 输入的depth需要在[0, 1]的范围
float2 ApplyEvsmExponents(float depth, float2 exponents)
{
depth = 2.0f * depth - 1.0f;
float2 expDepth;
expDepth.x = exp(exponents.x * depth);
expDepth.y = -exp(-exponents.y * depth);
return expDepth;
}
float2 EVSM2CompPS(float4 posH : SV_Position,
float2 texCoord : TEXCOORD) : SV_Target
{
uint2 coords = uint2(posH.xy);
float2 exponents = GetEVSMExponents(g_EvsmExponents.x, g_EvsmExponents.y, g_16BitShadow);
float2 depth = ApplyEvsmExponents(g_TextureShadow[coords].x, exponents);
float2 outDepth = float2(depth.x, depth.x * depth.x);
return outDepth;
}
float4 EVSM4CompPS(float4 posH : SV_Position,
float2 texCoord : TEXCOORD) : SV_Target
{
uint2 coords = uint2(posH.xy);
float2 depth = ApplyEvsmExponents(g_TextureShadow[coords].x, g_EvsmExponents);
float4 outDepth = float4(depth, depth * depth).xzyw;
return outDepth;
}
float CalculateExponentialVarianceShadow(float4 shadowTexCoord,
float4 shadowTexCoordViewSpace,
int currentCascadeIndex)
{
float percentLit = 0.0f;
float2 exponents = GetEVSMExponents(g_EvsmPosExp, g_EvsmNegExp, g_16BitShadow);
float2 expDepth = ApplyEvsmExponents(shadowTexCoord.z, exponents);
float4 moments = 0.0f;
float3 shadowTexCoordDDX = ddx(shadowTexCoordViewSpace).xyz;
float3 shadowTexCoordDDY = ddy(shadowTexCoordViewSpace).xyz;
shadowTexCoordDDX *= g_CascadeScale[currentCascadeIndex].xyz;
shadowTexCoordDDY *= g_CascadeScale[currentCascadeIndex].xyz;
moments += g_TextureShadow.SampleGrad(g_SamplerShadow,
float3(shadowTexCoord.xy, (float) currentCascadeIndex),
shadowTexCoordDDX.xy, shadowTexCoordDDY.xy);
percentLit = ChebyshevUpperBound(moments.xy, expDepth.x, 0.00001f, g_LightBleedingReduction);
if (SHADOW_TYPE == 4) // EVSM4
{
float neg = ChebyshevUpperBound(moments.zw, expDepth.y, 0.00001f, g_LightBleedingReduction);
percentLit = min(percentLit, neg);
}
return percentLit;
}
不得不说这个阴影效果还是可以的:

EVSM具有如下优点:
- 可以使用图片空间blur或硬件filtering来产生软阴影,也不需要开很大的Blur
- 相比前面的ESM、VSM,最大程度上减缓漏光问题
- 不需要处理shadow acne问题,因此也不需要引入depth bias
- 不需要使用很大的c,因此可以考虑使用16位float存储EVSM
但它也有如下缺点:
- EVSM4需要使用4个float,不仅占用了一定的带宽,而且进行混合需要消耗更多的时间,对移动端可能不友好
- 极端情况下,存在ESM和VSM同时无法解决的artifacts
阴影本身就是一个巨大的坑。总体来说,VSM和ESM这些尝试拟合最开头图像函数的方法都难以避免出现漏光的问题,对于具有复杂深度的场景表现不尽如人意。EVSM的总体效果更优,但对硬件要求也比较高。这些方法可以放在级联等级较大,即距离较远的地方,当然也有人在远距离尝试使用距离场,这些都是遥远的后话了。
建议读者直接打开项目进行尝试,这里只解释部分可调参数的含义:
- Light Bleeding:将
[0, amount]映射到0,将[amount, 1]映射到[0, 1] - Enable Mipmap:级联阴影开启mipmap
- Sampler:采样VSM使用的滤波
- Blur Sigma:高斯滤波用于控制权重分散情况
- Magic Power:控制\(e^{cd}\)和\(e^{cz}\)的c项
- Pos Exp:控制\(c_{pos}\)
- Neg Exp:控制\(c_{neg}\)
GPU Profile那边开Release来查看各个Pass下的用时。至于MSM等其它方法,可以尝试跑TheRealMJP/Shadows的项目,但需要一些动手修改的能力,它那边可以调的参数更多。
参考与扩展阅读材料如果有兴趣的话可以了解下面这些内容,当然肯定是有我没注意到的。
Fixed-Size Penumbra- PCF(Percentage Closer Filtering)
- VSM(Variance Shadow Maps, 2006)
- LVSM(Layered Variance Shadow Maps)
- ESM(Exponential Shadow Maps, 2008)
- EVSM(Exponential Variance Shadow Maps)
- MSM(Moment Shadow Maps, 2015)
- Virtual Shadow Map(这个估计只能在DX12做)
- PCSS(Percentage Closer Soft Shadows)
- VSSM = PCSS + VSM(Variance Soft Shadow Maps)
- SAVSM = VSM + SAT(Summed Area Table)
- 距离场阴影
- Reflective Shadow Maps
- 光线追踪白给的阴影,但需要显卡支持
- Sample Distribution Shadow Map
- GPU-Driven Cascade Setup and Scene Submission
- Deferred Shadow
[1]Cascade Shadow Maps--MSDN
[2]Playing with Real-Time Shadows(Siggraph 2013)
[3]Lighting Research at Bungie(Siggraph 2009)
[4]Advanced Soft Shadow Mapping Techniques(GDC 2008)
[5]Variance Shadow Maps(GDC 2006)
[6]A Sampling of Shadow Techniques
[7]论文:Layered Variance Shadow Maps
[8]KlayGE:切换到ESM
[9]Exponential Variance Shadow Maps
[10]知乎:方差阴影(Variance Shadow Map)实现
[11]知乎:Unreal Engine UE4 静态阴影实现 Static ShadowMap ESM,改进ESM(log space 下做模糊)
[12]Percentage-Closer Soft Shadows
[13]Integrating Realistic Soft Shadows Into Your Game Engine
[14]VSSM
[15]Moment Shadow Mapping (momentsingraphics.de)
[16]Sample Distribution Shadow Map(自动级联分层)
[17]知乎:影子传说——三种Shadowmap改进算法的原理与在Unity中的实现
参考项目:
VarianceShadows11
TheRealMJP/Shadows
DirectX11 With Windows SDK完整目录
欢迎加入QQ群: 727623616 可以一起探讨DX11,以及有什么问题也可以在这里汇报。
