无向图最小环问题解答

问题阐述：给出一个无向图，找出权值和最小的子图，其中子图的形式为简单环

解题思路，我们可以选取构建抽象模型{u,x1,x2,......xn,v,xm,.....u}作为满足条件的抽象环形结构，可知我们可选择图内任意两个点，围绕他们来做环。

我们的思路在于找到从u到v和从v到u的和值最小，即可以将问题分解为最短路问题。使用Floyd算法求最短路的思路（不清楚Floyd算法的话可转至此链接了解：https://oi-wiki.org/graph/shortest-path/#floyd），我们将集合划分为两部分，其中一部分是将1至k-1作为中继点找最短路。这时利用Floyd算法的推广我们将点k引入并连接求最短路并更新最小值。下图将证明这种推断的合理性。

 

 如本图所示，假设该图有n个节点，这里圈入的是标号1至n-1的节点（包括i和j）。我们可以证明此时如果以n为中继点可得到i与j的最短路i-j-n-i即为最小环。首先i-j是已包含节点内可使i与j连通的最短路，此时通过k连接i与j可以实现最短路的话便无法在1至n-1内寻找一个点满足最短路。因为这个点要么在已知最短路上（不满足成环条件），就是在路外（不满十足最短路条件）。所以这个结构迭代下去即可实现最小环的寻找。

例题：

P6175 无向图的最小环问题 https://www.luogu.com.cn/problem/P6175

题目截图如下：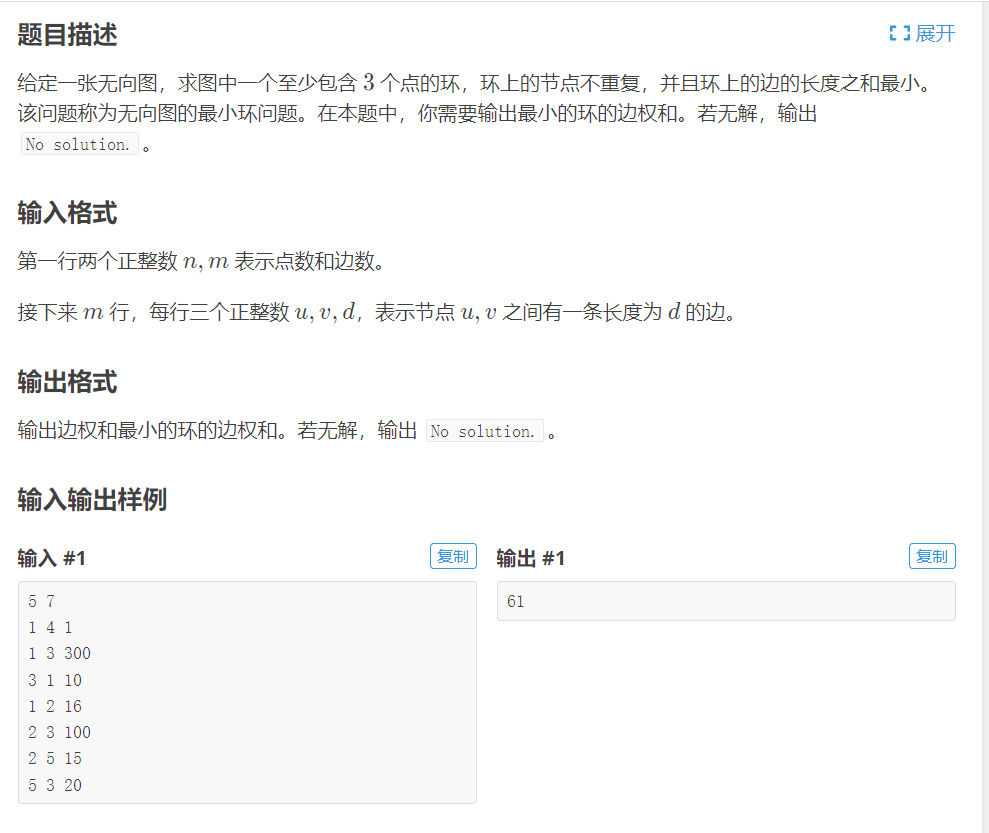

解题注意事项：此题为无向图最小环模板题，应注意重复边的判别。

 1 #include <cstdio>
 2 #include <iostream>
 3 #include <algorithm>
 4 #include <string.h>
 5 #define ll long long
 6 using namespace std;
 7 const int M=105;
 8 const int inf=0x7f7f7f7f;
 9 ll f[M][M],m[M][M];
10 ll ans=inf;
11 ll num_v,num_e;
12 void add(ll u,ll v,ll w){//双向加边 
13     f[u][v]=min(f[u][v],w);//重边判别 
14     f[v][u]=min(f[v][u],w);
15     m[u][v]=min(m[u][v],w);
16     m[v][u]=min(m[v][u],w);
17 }
18 int main(){
19     for (int i=0;i<105;i++){
20         for (int j=0;j<105;j++){
21             if (i!=j){
22                 f[i][j]=inf;
23                 f[j][i]=inf;
24                 m[j][i]=inf;
25                 m[i][j]=inf;
26             }
27         }
28     }
29     cin>>num_v>>num_e;
30     for (int i=1;i<=num_e;i++){
31         ll u,v,w;
32         cin>>u>>v>>w;
33         add(u,v,w);
34     }
35     for (int k=1;k<=num_v;k++){//k次迭代，做Floyd算法 
36         for (int x=1;x<k;x++){//x和y都应在1至k-1范围内 
37             for (int y=x+1;y<k;y++){
38                 ans=min(ans,f[x][y]+m[x][k]+m[k][y]);//与k点连接并更新 
39             }
40         }
41         for (int i=1;i<=num_v;i++){//具体的Floyd，扩大子图范围 
42             for (int j=1;j<=num_v;j++){
43                 f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
44                 f[j][i]=f[i][j];
45             }
46         }
47     }
48     if (ans==inf)
49         cout<<"No solution.";
50     else
51         cout<<ans;
52     return 0;
53 }

 

【本文来源：韩国服务器 http://www.558idc.com/kt.html欢迎留下您的宝贵建议】