题目链接:
本题需要求一个正奇边形可以被划分成多少个区域。
一、欧拉示性数公式:
V(n) + F(n) - E(n) = 2
V(n) -----> n边形的顶点数
F(n) -----> n边形的面数
E(n) -----> n边形的边数
定义C(n,m)为组合数在n个元素中取m个元素的方案数
把图转化成适用于欧拉示性数公式的图的形式:把所有交点当作顶点,把所有的边分割成小段。
二、V(n)求解:
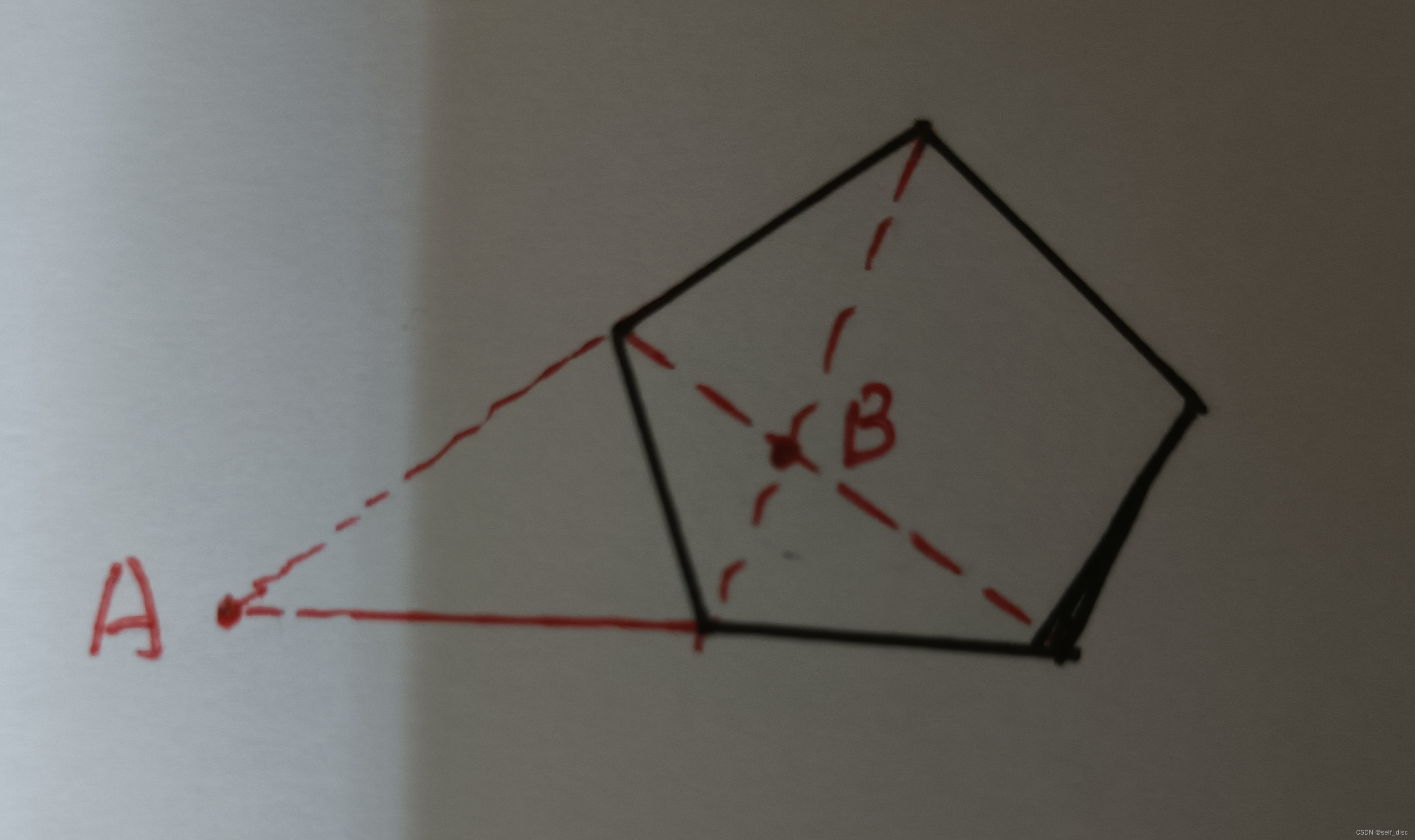
显然,因为两条线段为n边形上的边并且是正奇边形,所以不可能存在平行的情况,即一定会相交于一点,而且交点一定是新产生的点(两条边增加一个顶点),不可能是先前存在的顶点。交点有以下两种情况:
A类点和B类点,均为新增加的点。每个新增加的点需要四个点构成的两条直线相交得到,所以新增加的点的个数为C(n,4)(组合数),所以总的点数为:
V(n) = C(n,4) + n
三、E(n)求解:
考虑a条线交于b个点可以产生多少条小边?假设a-1条边互相平行,交于b个顶点,很容易得到新产生的边有2*b+a条,推广到一般情况发现都满足此关系,故而:
E(n) = C(n,2) + 2*C(n,4)
注:C(n,2)为变的个数,两个顶点确定一条边。
C(n,4)为交点的个数,不包含n边形的顶点。
四、到此V(n)和E(n)均求解完毕,由欧拉示性数公式有:
F(n) = E(n) - V(n) + 2
= C(n,2) + 2*C(n,4) - C(n,4) - n + 2
=C(n,2) + C(n,4) - n + 2
因为最后我们只求n边形内的图形区域数量,所以处于n边形外的区域即最终答案为F(n)-1
即:C(n,2) + C(n,4) - n + 1
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 1e9 + 7;
ll qpow(ll a, ll n)//快速幂a^n
{
ll ans = 1;
ll base = a;
while (n)
{
if (n & 1)
{
ans = ans * base % mod;
}
base = (base * base) % mod;
n >>= 1;
}
return ans;
}
ll C(int n, int m)//组合数求解C(n,m)
{
ll ans = 1;
for (int i = n; i >= n - m + 1; i--)
{
ans = (ans * i) % mod;
}
for (int i = 1; i <= m; ++i)
{
ans = (ans * qpow(i, mod - 2)) % mod;//逆元
}
return ans;
}
int main()
{
ll n;
scanf("%lld", &n);
printf("%lld\n", (C(n, 4) + C(n, 2) - n + 1 + mod) % mod);
return 0;
}参考: