隐私集合求交（PSI）-多方

本文主要讲解一个多方的PSI协议，文章转载：隐私计算关键技术：多方隐私集合求交（PSI）从原理到实现以及多方隐私求交——基于OPPRF的MULTI-PARTY PSI；原论文：Practical Multi-party Private Set Intersection from Symmetric-Key Techniques[ACM CCS 2017]；开源库

上次介绍了两方PSI协议：隐私集合求交（PSI）-两方，用到了cuckoo hash和OPRF技术，下面介绍的多方PSI在基于这些技术上进行改进。

问题

在绝大多数情况下，隐私计算的参与方是要多于3方的。因此我们更需要一种能够实现任意多方之间PSI的方法，同时在性能上也要能满足大量样本计算的要求。

多方PSI思路

我们假设有\(X\)个参与方，每个参与方都持有一些样本，所有的样本都是集合\(X\)中的元素。我们可以分两步完成多方样本交集的计算。为了方便说明原理，我们假设自己作为可信第三方，来协助各个参与方完成计算过程。而实际上的算法实现，就是用技术手段替代掉了这个可信第三方，保证整个过程中各个参与方都没有任何数据泄露给任何人。

有条件的秘密共享

这里的有条件的指的是有可信第三方

我们对集合\(X\)中的每一个元素，都随机生成\(n\)个数字（每个参与方一个数字），保证这\(n\)个数字的和是\(0\)。然后我们给\(n\)个参与方分发这些数字：如果参与方持有这个元素，我们就把生成的数字发给他，如果参与方没有持有这个元素，我们就随机生成另一个数字发给他。

这就是Zero-Sharing技术，具体如下：

可以看出，假如有一个元素是所有参与方都持有的，那么把所有参与方拿到的数字加起来，就是\(0\)。假如这个元素不是每个参与方都有，所有的参与方的数字加起来，就是一个随机数。

有条件的解密

对集合\(X\)中的每一个元素，询问每个参与方在上一步中得到的数字，并把得到的全部数字相加，如果结果为\(0\)，就表明所有参与方都持有这个元素（是PSI计算结果中的一个）。对\(X\)中的每个元素都执行这个过程后，我们就得到了多方PSI的结果。

忽略技术细节和这两个步骤的名字的话，多方PSI计算的原理，是不是还挺简单的。

但是我们是在可信第三方的协助下完成了计算，这个可信第三方是知道了每个参与方的全部样本数据的，这并不符合PSI的要求，即每个参与方的全部样本数据，不能对任何外部人泄露。所以，为了不泄露额外的信息，我们使用OPPRF协议来替代掉可信第三方，实现上述的有条件地秘密分享与解密两个步骤。

多方PSI+OPPRF

OPPRF是基于OPRF来构建的（少了一个Programmable，即可编程性），我们首先得了解OPRF，然后在OPRF的基础上扩展出OPPRF。

OPRF

OPRF的讲解在上篇文章已说过，如下图：

OPRF的全称是Oblivious Pseudo-Random Function，即不经意伪随机函数。

OPRF是一个两方的协议，协议中，一方为发送者\(S\)，一方为接收者\(R\)。协议运行前，接收者\(S\)有一系列输入\(q_1,q_2,...,q_t\)。运行OPRF协议之后，发送者\(S\)可以得到一个PRF（伪随机函数）\(F\)的密钥\(K\)，接收者\(R\)可以得到一系列伪随机函数的计算结果\(F(K,q_1),F(K,q_2),...,F(K,q_t)\)，同时，发送者\(S\)不知道接收者\(R\)的输入，接收者\(R\)也不知道发送者\(S\)得到的密钥\(K\)。这就好像是有一个“上帝”，随机选了个\(K\)作为PRF的密钥，把\(K\)发给了发送者\(S\)，然后计算了\(F(K,q_1),F(K,q_2),...,F(K,q_t)\)，并将他们发送给接收者\(R\)。当然，实际上不存在这样一个第三方的“上帝”，OPRF完全是由发送者\(S\)与接收者\(R\)两方实现的。

在上篇文章中使用OPRF实现了一个两方的PSI算法。

假设发送者\(S\)与接收者\(R\)分别持有\(a_1,a_2,...,a_n\)和\(b_1,b_2,...,b_m\)，他们要进行PSI，接收者[公式]可以把他持有的元素[公式]作为OPRF的输入，那么接收者\(R\)可以得到\(F(K,b_1),F(K,b_2),...,F(K,b_m)\)，发送者\(S\)已知\(K\)，在本地即可计算出\(F(K,a_1),F(K,a_2),...,F(K,a_n)\)。发送者\(S\)将本地计算的\(F(K,a_1),F(K,a_2),...,F(K,a_n)\)发送给接收者\(R\)，接收者\(R\)在本地与\(F(K,b_1),F(K,b_2),...,F(K,b_m)\)进行对比，即可完成PSI。在这个过程中，发送者[公式]全程没看到接收方\(S\)的输入，而接收方\(R\)看到的都是PRF的输出结果，无法反推输入，同时也没有密钥\(K\)，无法得到结果后暴力搜索，这就保证了PSI中两方的数据隐私。

OPPRF

OPPRF的全称是Oblivious Programmable Pseudo-Random Function，即可编程的不经意伪随机函数。与OPRF相比，多了一条可编程的性质，即发送者\(S\)可以设置PRF在某些点上的输出，这些点以及PRF的输出由发送者\(S\)选定。先不管是怎么实现的，反正OPPRF可以实现这样的功能：

我有三个数据：\(a,b,c\)，当别人来找我查数据，如果别人查的是这三个中的一个，我就返回一个预先定义好的数字，如果别人查的不是这三个中的一个，我就返回一个随机数。并且，我全程不知道别人查的是什么，他也不知道拿到的到底是随机数还是预先定义好的结果。

这个功能看起来，是不是和之前PSI原理的第一步特别相关。正是通过OPPRF实现的这个功能，我们做到了在不暴露各个参与方的数据的前提下，完成了秘密分享的分发。

下面具体讲一讲OPPRF算法：

OPPRF的正确性：

OPPRF需要保证，对于\((x,y)\in P,(k,hint)\leftarrow P,F(k,hint,x)=y\)一定成立。

类似OPRF，OPPRF的机制可以这么描述：发送者\(S\)有一系列点 \(P=(x,_1,y_1),(x_2,y_2),...,(x_n,y_n)\)，接收者\(R\)有一系列输入\(q_1,q_2,..,q_t\)，运行OPPRF后，发送者\(S\)得到了\(KeyGen(P)\)的输出\((k,hint)\)，接收者\(R\)得到了\(F(k,hint,q_1),F(k,hint,q_2),...,F(k,hint,q_t),\)以及\(hint\)。

OPPRF的安全性：

相比OPRF，OPPRF的接收者\(R\)额外获得了一部分信息，即\(hint\)，而\(hint\)是根据发送者的输入\(P\)生成的，这可能会带来一些额外的安全隐患。
所以，在安全性上，OPPRF需要保证，即使得到了\(hint\)以及PRF在\(q_1,q_2,..,q_t\)上的输出，接收者\(R\)也无法区分出某个点\(x\)是否属于\(P\)（前提是\(P\)中的\(y_1,y_2,...,y_n\)都是随机的，不能是一个固定的值）。这一点，我们称为OPPRF的安全性。安全性其实隐含了对于不属于\(P\)的点\(x\)，PRF在\(x\)上的输出也是随机的。

由于OPPRF与OPRF的形式很类似，只是多了个\(hint\)，所以，OPPRF是在OPRF的基础上构建的。OPPRF有多种构建方式，他们的区别只是在如何构建\(hint\)，以及如何使用\(hint\)来保证正确性。

下面，我们介绍三种不同的OPPRF构建方式。

基于多项式的

首先，我们介绍基于多项式构建的OPPRF的两个算法：

显然，上述算法是满足OPPRF的正确性的。对于

\[(x_i,y_i)\in P,\widehat{F}(k,hint,x_i)=F(h,x_i)\bigoplus p(x_i)=F(h,x_i)\bigoplus y_i \bigoplus F(h,x_i)=y_i \]

在安全性上，只要\(y_i\)是随机选择的，那么多项式\(p(x)\)的系数也是随机的，对于任意的点\(x\notin P\)，\(p(x)\)的值也都是随机的，因此，上述算法满足OPPRF的安全性。

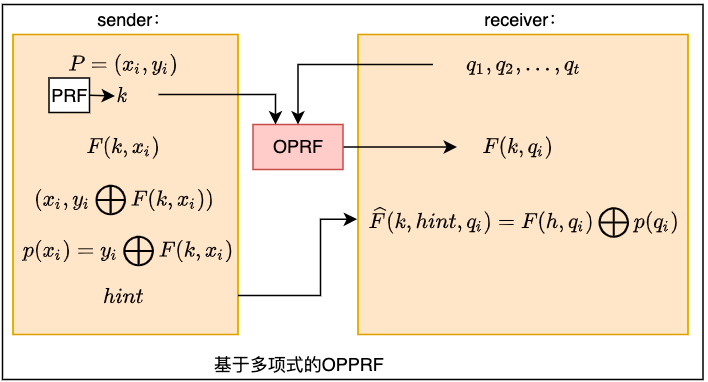
想要用OPRF来实现上述两个算法，非常简单。我们可以先在发送者\(S\)和接收者\(R\)之间，运行一次OPRF，发送者\(S\)得到密钥\(k\)，接收者\(R\)得到\(F(k,q_i)\)，\(q_i\in (q_1,q_2,...,q_t)\)。然后，发送者\(S\)根据密钥\(k\)以及点集\(P\)计算\(hint\)，并将\(hint\)发送给接收者\(R\)，接收者\(R\)根据\(hint\)，计算\(\widehat{F}(k,hint,q_i)=F(h,q_i)\bigoplus p(q_i)\)。

这种方法构造的OPPRF，计算开销很大\(O(n^2)\)，通信开销很小\(n\)。

在计算开销上，计算多项式插值的开销是\(O(n^2)\)，当点集\(P\)很大时，这个开销会非常大。但是，这种方法的传输开销很小，\(hint\)是多项式的系数，大小为\(n\)，不可能有比这个更小的传输开销了。

基于布隆过滤器的

首先介绍一下混淆布隆过滤器（Garbled Bloom Filter， GBF），这里的介绍也不是很清晰:

GBF是一个长度为\(N\)的数组\(G\)，配合\(k\)个哈希函数\(h_1,h_2,...,h_k:{0,1}^*\rightarrow [N]\)。用GBF可以实现键值对存储的功能，对于一个键\(x\)， 其对应的值为\(\bigoplus _{j=1}^{k}G[(h_j(x))]\)。

我们可以先在发送者\(S\)和接收者\(R\)之间，运行一次OPRF，发送者\(S\)得到密钥\(k\)和\(F(k,x_i)\)，接收者\(R\)得到\(F(k,q_i)\)，\(q_i\in (q_1,q_2,...,q_t)\)。
可以按照如下方法，将一个\((x_i,y_i\bigoplus F(k,x_i))\)插入到GBF中：

下面的描述就有点不懂了，有点乱！

• 将长度为\(N\)的数组\(G\)中的每个元素，初始化为空，记为\(null\)。
• 对于每一个键值对\((x,y)\)，设\(J=(h_i(x)|G[h_i(x)],j\in [k])\)为\(x\)对应的位置，如果\(J\)位置不为空，退出；否则，为\(G[j],j\in J\)赋随机值，使得等式\(y=\bigoplus _{j=1}^{k}G[(h_j(x))]\)成立。
• 对于数组\(G\)中仍然为空的位置，给它们赋上随机值。

我们可以看出，除非GBF在插入的过程中退出，那么GBF就可以实现储存键值对的功能，同时无法从GBF中推测出其是否包含键\(x\)。使用GBF实现OPPRF与基于多项式的实现方法类似，只是将多项式插值，改为将点集\((x_1,y_1\bigoplus F(k,x_1)),(x_2,y_2\bigoplus F(k,x_2)),...,(x_n,y_n\bigoplus F(k,x_n))\)插入GBF，并将GBF作为\(hint\)，发送给接收者\(R\)。显然，这样的实现是满足OPPRF的正确性与安全性的。

使用GBF的问题是，在插入的过程中，有可能会因为\(J\neq 0\)而退出。这个退出的概率，与GBF的数组长度\(N\)，以及插入的元素个数\(n\)是相关的。具体来说，如果想要将退出的概率控制在\(2^{\lambda }\)以下，则需满足\(N=n.\lambda .loge\)。 假设\(\lambda =40\)，则可以设\(N=60n\)，同时\(k=40\)，即40个哈希函数。

基于布隆过滤器的OPPRF，计算开销为\(O(n)\)；通信开销为\(O(n)\)

在计算开销上，插入GBF的开销是\(O(n)\)，相比多项式插值的\(O(n^2)\)要高效很多。在传输开销上，也是\(O(n)\)，但是其系数非常大（需要传输\(60n\)，而不是\(n\)），当\(n\)很大时，这很可能会成为算法的瓶颈。

基于hash的

先简单介绍一下，基于哈希表构造OPPRF的大致思路。

首先，发送者\(S\)与接收者\(R\)之间，运行OPRF协议，发送者\(S\)得到\(F(k,x_i),i\in [n]\)，接收者\(R\)得到\(F(k,q)\)。发送者\(S\)使用\(F(k,x_i)\)作为加密的密钥，来加密\(x_i\)对应的\(y_i\)。把加密得到的密文集合\(T\)作为OPPRF的\(hint\)，发送给接收者\(R\)。接收者\(R\)使用\(F(k,q)\)解密\(T\)中某一个对应的密文，得到结果。

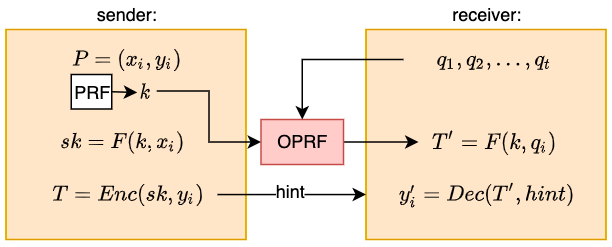
在上述思路中，主要的难点在于：

• 不能让接收者\(R\)知道它解密出来的结果，是一个随机值，还是某个\(y_i\)。
• 必须让接收者\(R\)知道，它应该解密\(T\)中的哪个密文。

想要解决难点2，我们可以让\(T\)变成一个哈希表，每一个\(F(k,x_i)\)对应哈希表中的一个位置，这样接收者\(R\)就可以根据\(F(k,q)\)的值，找到哈希表中对应的密文，进行解密。

要解决难点1，我们需要让接收者\(R\)在密钥不对的情况下，也能解密出一个随机值，而不是直接解密失败，这样，接收者\(R\)就无法区分解密出的是随机值还是\(y_i\)了（因为\(y_i\)本身就是一个随机值）。要想达到这一点，我们可以使用one time pad加密。不过，要使用one time pad加密，我们就需要保证接收者\(R\)只能有一个\(q\)，否则如果多个不同\(q\)对应到了哈希表\(T\)中的同一个位置，就可能造成重用密钥，从而破坏one time pad的安全性。

有了上述的思路之后，我们来看具体的实现。假设\(n=20\)，即发送者\(S\)有20对\((x_i,y_i)\)，那么发送者构造一个大小为32的哈希表\(T\)（32为大于20的最小的2的幂次）。发送者\(S\)随机选取一个nonce (随机数)\(v\)，使得\(H(F(k,x_i)||v)\)中每个元素，都互不相同，其中\(H:{0,1}^*\to {0,1}^5\)是一个哈希函数。对于每个\(x_i\)，发送者\(S\)计算\(h_i=H(F(k,x_i)||v)\)，并且设\(T[h_i]=H(F(k,x_i))\bigoplus y_i\)。对于哈希表\(T\)中其余的12个位置，放入随机值。将表T和nonce \(v\)发送给接收者\(R\)，接收者\(R\)可以计算出，\(T[h_i']\bigoplus F(k,q)\)就是结果。

综上，基于哈希表的OPPRF的两个算法为：

显然，上述算法是满足OPPRF的正确性的。

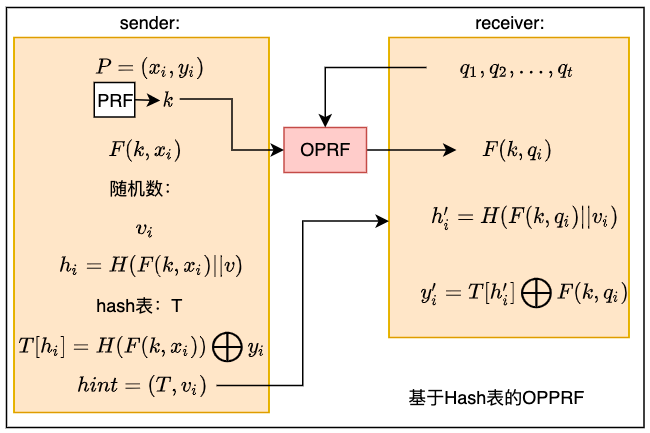
在安全性上，因为\(hint\)现在包含哈希表\(T\)和nonce \(v\)，我们需要分别考虑这两部分的安全性。对于哈希表\(T\)来说，只要\(y_i\)是随机选取的，那么\(T\)中的所有元素，也都是随机的，不会暴露发送者\(S\)的信息。对于\(v\)来说，我们需要证明的是，接收者\(R\)无法通过\(v\)来判断，他持有的元素\(q\)是否在发送者\(S\)的集合\(p\)中。对于PRF函数\(F()\)来说，某一个\(F(k,x_i)\)与其他的输出，是互相独立的。由于哈希函数\(H\)的性质，某一个\(H(F(k,x_i)||v)\)与其他的点也是互相独立的。因此，是否选择某个\(v\)，与任意一个单独的\(x_i\)都是独立的。由于接收者\(R\)只有1个\(q\)，所以\(v\)的选择对于\(q\)来说，也是独立的。因此，发送\(v\)给接收者\(R\)是安全的。

相比之前的两种构造方法，基于哈希表的构造，在计算开销和传输开销上都十分有优势。

在传输开销上，\(T\)的大小是\(O(n)\)，常数最坏情况也只是2，外加一个固定长度的\(v\)。在计算开销上，一共需要计算\(n\tau\)次哈希函数\(H\)，这里\(\tau\)是选择nonce \(v\)的次数。虽然最差情况下\(\tau\)可能很大，但是当\(n\)很小的情况下，\(\tau\)也会很小，因此整体计算开销也很小。

有条件的秘密分享

在之前的原理介绍中，有条件的秘密分享要对整个样本空间\(X\)中的元素生成秘密分享，但是实际实现中，只要每个参与方\(P_i\)对自己持有的样本集合\(X_i\)中的元素生成秘密分享就可以了。

假设有n个参与者

准确的来说，每个参与方\(P_i\)对自己持有的样本集合\(X_i\)中的每个元素\(x_k^i\)，生成\(n\)个秘密分享\(x_k^{i,1},x_k^{i,2},...,x_k^{i,n}\)，使得\(x_k^{i,1}\bigoplus x_k^{i,2}\bigoplus ...\bigoplus x_k^{i,n}=0\)。

然后，在每一对参与者\(P_i\)与\(P_j\)两两之间，运行OPPRF。\(P_i\)作为发送者，\(P_j\)做为接收者。接收者\(P_j\)对于自己持有的每一个样本\(x_k^{j}\in X_j\)，去发送者\(P_i\)获取对应的秘密分享。OPPRF保证了当发送者\(P_i\)也持有这个样本的时候\(x_k^{j}\in X_i\)，接收者\(P_j\)得到了\(x_k^{i,j}\)，否则$P_j $得到的就是一个随机值。

\(P_j\)作为接收者，需要和其他全部的\(n-1\)个参与方\(P_i\)运行OPPRF协议。对于每个\(x_k^{j}\in X_j\)，它都能从\(n-1\)个发送方\(P_i\)处收到一个\(P_i\)的分享值\(\widehat{s}_k^{i,j}\)，还有自己生成的分享值，一共\(n\)个。\(P_j\)将这些分享值全部异或起来，做为自己的针对样本\(x_k^j\)的秘密分享，即\(S_j(x_k^j)=\bigoplus_{i=1}^{n}\widehat{s}_k^{i,j}\)，其中\(\widehat{s}_k^{i,j}\)是\(P_j\)自己生成的\(x_k^j\)的分享值）。

每个参与方，都要做为接收者，和其他全部参与方执行上面的步骤，得到自己的秘密分享\(S_j(x_k^j)\)。如果每个参与方都持有元素\(x\)，那么\(\bigoplus_{j=1}^{n}S_j(x)=0\)。这样，每个参与方\(P_j\)记下元素\(x_k^j\)对应的\(S_j(x_k^j)\)，就实现了有条件的秘密分享。

有条件的解密

这里要选出一个leader收集秘密分享，例如\(P_1\)

接下来，我们就可以进行有条件的解密了。这一步我们需要挑选一个参与方来收集大家的秘密分享，计算出最终的PSI的结果，再发给大家。不失一般性，我们挑选\(P_1\)来作为解密的那个人。

解密的计算本身很简单，对于\(P_1\)所持有的每一个样本\(x_k^1\)，从其他全部参与方那里获取对应的秘密分享的值\(S_j(s_k^j)\)，把全部的值，和自己的值一起，异或起来，如果是\(0\)，说明这个样本\(x_k^1\)是所有参与方共有的，\(P_1\)对自己的每一个样本都执行上述操作，最后得到的全部异或为\(0\)的元素的集合，就是最终的PSI结果。

但是如果只是这样计算的话，同样暴露了\(P_1\)的全部样本，以及其他参与方是否有某个样本的额外信息，因此这一步，仍然需要用OPPRF来实现。\(P_1\)作为接收者，对于自己的每一个样本，都和全部参与方执行OPPRF协议，发送方如果有这个样本，就发送真实的秘密分享的值，如果没有，就发送随机值。这样\(P_1\)对于结果的判断方法不变，同时保证了包括\(P_1\)在内的各方持有的集合都不对外泄露。

算法的正确性和安全性

假阳性：可以看作错误率，一般出现在cuckoo hash时，可以通过调参，控制假阳性。

在正确性上，这种构造方法是有可能出现假阳性（false positive）的情况的，即某个\(x\)不属于所有参与方的交集，但是[公式]依然成立。出现假阳性的概率，与在Cuckoo Hashing中无法插入元素的概率$\lambda $相关，所以只要根据每个参与方集合的大小，合理设置Cuckoo Hashing表的大小，就可以将假阳性的概率控制在一个很小的范围内。关于Cuckoo Hashing我们会在下文介绍OPPRF的原理时详细介绍。

安全性：抵抗半诚实的接收者

对于安全性而言，我们这里先给出结论，上述的构造在半诚实的模型下，可以在至多\(n-1\)个串谋的恶意参与方情况下，保证安全。这里，半诚实的模型，意思是那些串谋的恶意参与方，也会按照协议的要求，正常执行，只不过会尽力去窥探其他诚实方的数据。这里安全的意思是，串谋的恶意参与方，无法得知哪一个诚实方持有元素\(x\)，哪一个没有持有\(x\)。这一点其实不难证明。大体的思路是，只要有一个参与方不持有\(x\)，那么在OPPRF中，其他参与方对\(x\)的输出必然是一个随机值，由于在有条件的秘密分享中，每一个\(P_j\)的最终的秘密分享\(S_j(x)\)，都是由所有参与方的\(s_k^{i,j}\)异或得到，只要有一个\(s_k^{i,j}\)是随机的，那么所有人的\(S_j(x)\)看起来就都是随机的，无法区分，那么在有条件的解密时，就无法区分一个\(S_j(x)\)与一个随机值，这就保证了安全。

在效率上，在有条件的秘密分享阶段，每一对参与方之间，都需要运行一次OPPRF协议，总共需要\(O(n^2)\)次OPPRF协议；在有条件的解密阶段，只有一个参与方作为解密方，总共需要运行\(n-1\)次OPPRF协议。我们可以将每个OPPRF协议并行化地运行，这样可以使得协议整体的运行轮次固定下来，与参与方数量和每个参与方输入的大小无关。至于OPPRF的开销，我们会在后续章节详细介绍。

PSI+OPPRF+Cuckoo hash

上面，我们对比了3中不同的OPPRF实现方式，其中基于哈希表的实现，在计算开销和传输开销上，平衡的最好。但是，基于哈希表的实现，限制也是最大的，不仅要求接收者\(R\)只能有一个\(q\)（即\(t=1\)），同时要求发送者\(S\)的点集大小\(n\)不能太大，才能达到很高的计算效率。在实际的应用场景中，这显然是不现实的。所以，我们需要使用Cuckoo Hashing，来使基于哈希表的OPPRF能满足\(n\)与\(t\)很大的情况。

从宏观上将，我们需要发送者\(S\)和接收者\(R\)都将它们持有的集合映射到一个哈希表中去，哈希表中的每个位置对应接收者\(R\)的某一个\(q\)，以及一小部分的发送者\(S\)的的\(P\)，这样，就将\(n\)与\(t\)很大的情况下的OPPRF，分解为很多个小的OPPRF。在这里，我们使用Cuckoo Hashing来实现这种哈希映射。

Cuckoo hash

布谷鸟hash在上篇文章已经介绍过，更多请参考上一篇

这里先简单介绍一下Cuckoo Hashing（布谷鸟哈希）。
Cuckoo Hashing用\(k\)个哈希函数\(h_1,h_2,...,h_k\)，将元素放入\(m\)个桶中。对于一个元素\(q\)，我们计算\(h_1(q),h_2(q),...,h_k(q)\)，如果这些桶中有空的桶，就将\(q\)放入其中一个空桶中，结束插入；如果\(k\)个桶都有元素，就从中随机选择一个桶，踢出原来桶中的元素\(\widehat{q}\)，把\(q\)放入这个桶中，然后循环插入\(\widehat{q}\)，直至结束，或者到达循环次数的上限。
对于达到循环次数上限的元素，Cuckoo Hashing的不同变体，有不同的处理方式。在文章[2]中，他们使用一个额外的stash来储存达到循环次数上限的元素，但是这样做，会导致stash中有很多元素，这些元素都需要与对方进行对比，不够高效。

这里使用两个hash表来存储：

在这里，为了保证Cuckoo Hashing中每一个桶都只包含一个元素，我们使用另一个额外的Cuckoo Hashing表来替代stash，储存这些达到循环次数上限的元素。简单来说，我们有主副两个Cuckoo Hashing表，主表使用3个哈希函数，副表使用2个，当一个元素在主表中达到插入上限时，将他插入到副表中。当主表和副表的大小设置合理时，可以使得主表副表都无法插入一个元素的概率，不超过\(2^{-\lambda }\)。

现在来看如何使用Cuckoo Hashing扩展OPPRF。

首先，发送者\(S\)与接收者\(R\)使用相同的哈希函数，以及表的大小。接收者\(R\)使用Cuckoo Hashing，将持有的\(t\)个元素\(q_i\)，映射到哈希表中，表中每个位置都只有至多一个元素。对于表中空的位置，则赋一个随机值。
对于发送者\(S\)，将它持有的\(n\)个\(x_i\)，使用与接收者\(R\)相同的\(k\)个哈希函数，映射到表中\(h_1(x_i),h_2(x_i),...,h_k(q_i)\)的位置，即一个元素，插入哈希表\(k\)次。这样，发送者\(S\)与接收者\(R\)的哈希表每个位置一一对应，都包含一个\(q\)与数量很小的几个\(x_i\)，我们只需为哈希表的每个位置，构造一个OPPRF即可。

需要注意的是，发送者\(S\)的表中，每个位置包含的元素大小不同，而且有可能有空的位置，这会暴露一些信息，并不安全。所以，我们可以根据表的大小、元素个数\(n\)以及哈希函数的数量\(k\)，计算出表中每个位置包含元素数量的上限\(\beta\)，然后把发送者\(S\)的表中每个位置都填充上随机值，使每个位置都包含\(\beta\)个元素。

优化 无条件的秘密分享

在之前的多方PSI构造中，我们可以看到，有条件地秘密分享，需要\(O(n^2)\)次OPPRF，即使并行化，也依然是一个很大的通信开销。这一步，如果放宽安全条件，其实是可以进行优化的。如果我们的安全条件放宽到至多\(n-2\)个串谋的参与方，也就是至少2个诚实的参与方的情况下，可以使用无条件地秘密分享，来替代有条件地秘密分享。

下面没看太明白，以后补充

合并hint

在使用Cuckoo Hashing扩展OPPRF的时候，我们会发现，发送者\(S\)中的每个元素，都在Cuckoo Hashing的哈希表中出现了多次，也就会出现在多个OPPRF实例的\(hint\)中，这造成了一定传输开销的浪费。我们可以通过将这些\(hint\)合并起来，减少传输开销：

• 对于基于多项式的OPPRF构造，我们可以针对哈希表中的每个桶中的元素，计算一个多项式插值，因为每个桶中的元素很少，这大大减少了计算多项式插值的开销，但是会增大传输开销；也可以针对Cuckoo Hashing中的每个哈希函数，计算一次多项式插值，这使得\(hint\)的数量减少到\(k\)个，减少了传输开销，但是当元素数量很多时，计算开销很大。
• 对于基于GBF的OPPRF构造，由于每个元素在Cuckoo Hashing的哈希表中出现了\(k\)，所以需要插入\(k\)次键值对\((x,y\bigoplus F(k_{h_i},x))\)，这会使GBF所需的空间变大。作为替代，可以在GBF里插入\((x,(y\bigoplus F(k_{h_1},x)\bigoplus(y\bigoplus F(k_{h_2},x)\bigoplus...\bigoplus(y\bigoplus F(k_{h_k},x))\)，即将这些键值对中的值拼接起来一起插入，这可以节省GBF的空间。

参考

[1] Kolesnikov V, Matania N, Pinkas B, et al. Practical multi-party private set intersection from symmetric-key techniques[C]//Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. 2017: 1257-1272.

[2] Kolesnikov V, Kumaresan R, Rosulek M, et al. Efficient batched oblivious PRF with applications to private set intersection[C]//Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. 2016: 818-829.

[3] Freedman M J, Ishai Y, Pinkas B, et al. Keyword search and oblivious pseudorandom functions[C]//Theory of Cryptography Conference. Springer, Berlin, Heidelberg, 2005: 303-324.