【AcWing】AcWing 342. 道路与航线 （DAG）（拓扑排序，dijkstra）

原题：https://www.acwing.com/problem/content/344/

有负权边，一眼SPFA。然而好惨一SPFA QAQ 又被卡了

分析：

1. 道路：双向，边权非负
2. 航线：单向，边权可正可负，无环

y总做法：

1. 把只有道路连接的看作一个“团”
2. 团与团之间用航线连接，（根据航线特点）就构成了一个有向无环图（把每个团视作一个点），这个图就可以用拓扑排序来处理
3. 算法：（团内）dijkstra，（团与团之间）先拓扑排序再dijkstra

• 看看图：
  

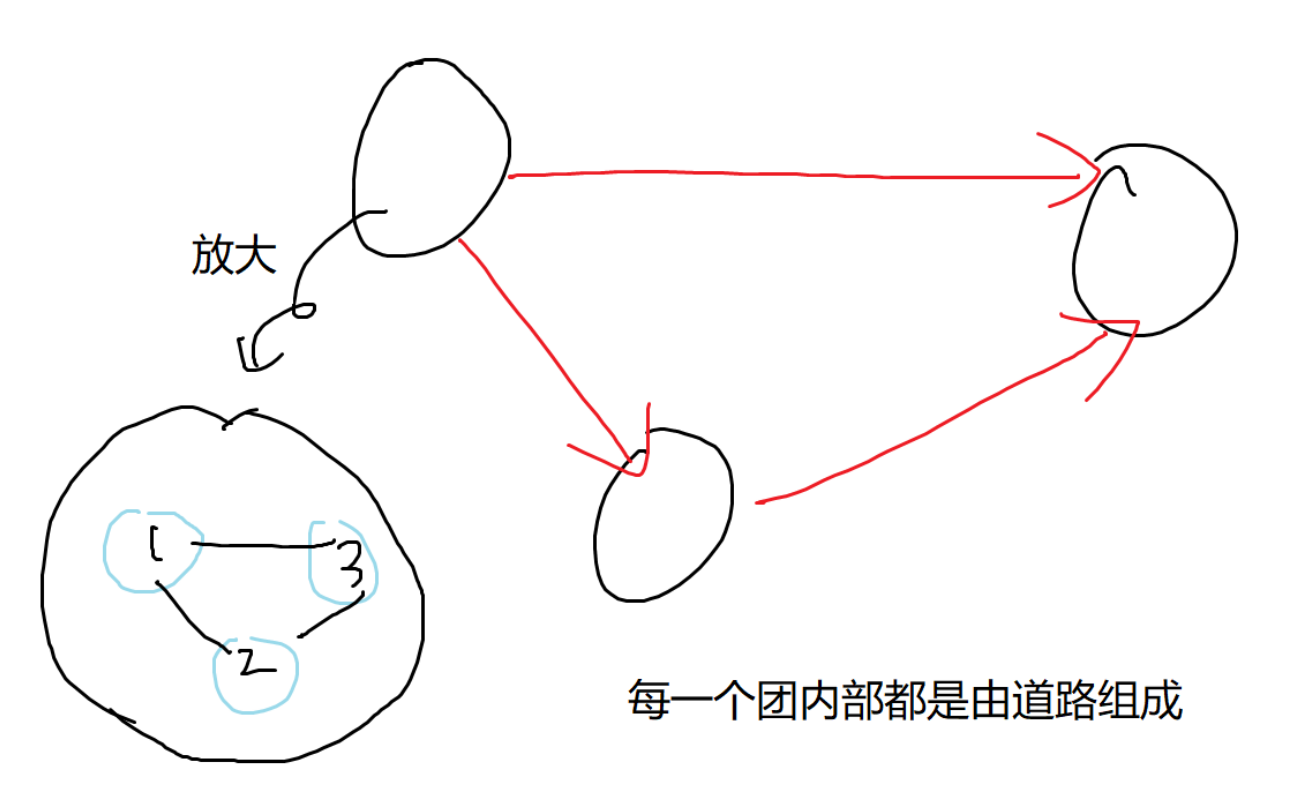
区域之间：按照拓扑序进行dijkstra

总结（大框架）：$dfs\rightarrow dijkstra\rightarrow topsort $

• 拓扑排序复习（因为苯人忘了怎么写）：

拓扑排序

这有一篇写得很好的题解

1. 有向无环图（一定至少有一个入度为0的点）一定有拓扑序，有向有环图一定无拓扑序
2. 如何得到拓扑序：每次都将入度为0的点入列，再删去该点所指向的所有边（入队的点的顺序就是拓扑序）
3. 拓扑序可以有多种

• 对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。

bool topsort(){
    queue<int> q;
    int t;
    for(int i = 1;i <= n; ++i)// 将所有入度为0的点加入队列
        if(d[i] == 0) q.push(i);
    while(q.size()){
        t = q.front();//每次取出队列的首部
        top[cnt] = t;//加入到 拓扑序列中
        cnt ++; // 序列中的元素 ++
        q.pop();
        for(int i = h[t];i != -1; i = ne[i]){
            // 遍历 t 点的出边
            int j = e[i];
            d[j] --;// j 的入度 --
            if(d[j] == 0) q.push(j); //如果 j 入度为0，加入队列当中
        }
    }
    if(cnt < n) return 0;
    else return 1;

}

必备技能：堆优化版dijkstra

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
#include <vector>

using namespace std;
typedef pair<int, int> pii;
const int N = 25005, M = 50005 * 3;
int n, m1, m2, s;
int h[M], e[M], ne[M], w[M], idx;
int dis[M], du[M];  //du[]表示该点入度
bool vis[N];
int id[N]; //表示在哪个团里
vector<int> block[N];  //储存团内点
queue<int>q;  //团与团之间的队列
int cnt; //统计有几个团

void add (int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

//dfs找连通块，构建团
void dfs (int u, int bid) {
    id[u] = bid;
    block[bid].push_back (u);

    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!id[j])  //如果这个点还没有入团
            dfs (j, bid);
    }
}

//大dijkstra套小dijkstra
void dijkstra (int bid) {
    priority_queue <pii, vector<pii>, greater<pii>>hq;  //团内部的堆

    for (auto i : block[bid])
        hq.push ({dis[i], i});
    //由于t图中每个点的编号都不同，所以不用将vis置false

    while (!hq.empty()) {
        auto t = hq.top();
        hq.pop ();
        int ver = t.second, dist = t.first;

        if (vis[ver])   continue;
        vis[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i]) {
            int j = e[i];
            if (id[j] != id[ver] && --du[id[j]] == 0)
                q.push (id[j]);  //更新团之间的拓扑图
            if (dis[j] > dist + w[i]) {
                dis[j] = dis[ver] + w[i];
                if (id[j] == id[ver])
                    hq.push ({dis[j], j});  //确保在团内部才更新，防止出现负权边
            }
        }
    }
}

void topsort () {
    memset (dis, 0x3f, sizeof dis);
    dis[s] = 0;

    for (int i = 1; i <= n; i ++)
        if (!du[i])
            q.push (i);  //入度为0则入队

    while (!q.empty()) {
        int t = q.front();
        q.pop();
        dijkstra (t);  //对现有的top图进行一个dijkstra
    }

}

int main () {
    memset (h, -1, sizeof h);
    cin >> n >> m1 >> m2 >> s;

    while (m1 --) {
        int x, y, z;
        cin >> x >> y >> z;
        add (x, y, z), add (y, x, z);
    }

    for (int i = 1; i <= n; i ++) {
        if (!id[i]) {
            cnt ++;  //团数++
            dfs (i, cnt);
        }
    }

    while (m2 --) {
        int x, y, z;
        cin >> x >> y >> z;
        du[id[y]] ++;  //x指向y, 所以y的入度++
        add (x, y, z);
    }

    topsort();

    for (int i = 1; i <= n; i ++) {
        if (dis[i] > 0x3f3f3f3f / 2)  //不连通
            cout << "NO PATH" << endl;
        else
            cout << dis[i] << endl;
    }
}

更好的阅读体验bushi