移动通信笔记-小尺度衰落和多径效应

移动无线电传播：小尺度衰落和多径效应 Chapter 5 小尺度衰落和多径效应 5.1小尺度多径传播

无线信道的多径传播导致小尺度衰落，表现为：

• 信号强度经过短距离/短时延后急剧变化
• 不同多径分量上，存在时变的多普勒（Doppler）频移引起的随机频率调制
• 多径传播时延引起的时间弥散

5.1.1影响小尺度衰落的因素

• 多径传播：信号的多个路劲分量以非相干的形式叠加
• 移动台/环境物体的相对运动：由多普勒频移引起的信道相干时间
• 信号的传输带宽：比较信号带宽与多径信道相干带宽的关系

5.1.2多普勒频移

• 传播过程中，路程差造成接收信号相位变化

\[\Delta\phi=\frac{2\pi\Delta l}{\lambda}=\frac{2\pi v\Delta t}{\lambda}\cos\theta \]

• 对应的频率变化值（多普勒频移）

\[f_d = \frac{1}{2\pi}\centerdot\frac{\Delta\phi}{\Delta t}=\frac{v}{\lambda}\centerdot\cos\theta \]

• 多普勒频移的绝对数值并不大，但结合多径传播引起的频谱展宽是需要重点考虑的因素。

5.2时变无线信道的通用表示式

 时变信道的冲激响应可以记为

\[h(\tau,t)=\sum_{n=0}^{N(t)}{\delta(\tau-\tau_n(t))\alpha_n(t)e^{j\phi_n(t)}} \]

• 由冲激函数、幅度增益和相位旋转构成了时变信道的通用模型
• 其中相位旋转由信道的多普勒偏移和传播延迟共同决定。

5.3无线信道的物理属性

\[时延扩展，相干带宽\leftarrow^{固定时间，研究时延}\longleftarrow h(\tau,t) \longrightarrow^{固定时延，研究时间}\rightarrow Doppler扩展，相干时间 \]

5.3.1时延扩展，相干带宽

 接收信号由多个可分辨的独立多径信号组成，造成了接收信号持续时间比该信号发送时的持续时间长（因为某些路径长的，那么它的到达接收机的时间就会比较长），造成了时域上的时间色散，用时延扩展来衡量；在频域上反映为频率选择性衰落，用相干带宽衡量。
（1）时延扩展[second]：最后到达接收机的信号与最先到达接收机的信号之间的时间差。
（2）相干带宽：约等于时延扩展的倒数，但是在一般的情况下，要确定多径信道对某一特定信号的精确影响，需要用到频谱分析技术与仿真。当两个频率分量的频率间隔小于相干带宽时，它们具有很强的幅度相关性。

5.3.1.1时间色散参数

时间色散参数通常用平均附件时延(\(\overline{\tau}\)）和RMS时延扩展(均方根时延扩展\(\sigma_{\tau}\))表示。

功率延迟分布PDP图

• 平均附加时延（mean excess delay）(功率延迟分布的一阶矩)

\[\overline{\tau}=\frac{\sum_{k}{a^2_k\tau_k}}{\sum_{k}{a^2_k}}=\frac{\sum_{k}{P(\tau_k)\tau_k}}{\sum_{k}{P(\tau_k)}} \]

• RMS时延扩展（rms delay spread）\(\sigma_{\tau}\)（功率延迟分布的二阶矩）

\[\sigma_{\tau}=\sqrt{\overline{\tau^2}-{\overline{\tau}}^2} \]

 其中\(\overline{\tau^2}=\frac{\sum_{k}{a^2_k\tau_k^2}}{\sum_{k}{a^2_k}}=\frac{\sum_{k}{P(\tau_k)\tau_k^2}}{\sum_{k}{P(\tau_k)}}\)

• 则可知RMS时延扩展依赖于多径分量的相对幅度
   补充：
  由于信道的功率分布具有随机性，因此需要采用大量信道响应，实现功率分布的平均。
  此时
  \(\overline{\tau}=\int^{\infty}_0{\tau f(\tau) d \tau}\) 且 \(\sigma_{\tau}=\sqrt{\int({\tau-\overline{\tau})^2 f(\tau) d \tau}}\)
  常见信道的PDP是单边指数分布(如瑞利信道)

\[f(\tau) = \frac{1}{\overline{\tau}}e^{-\frac{\tau}{\overline{\tau}}},\tau > 0 \]

其均方根时延扩展为
\(\sigma_{\tau}=\sqrt{\int({\tau-\overline{\tau})^2 f(\tau) d \tau}}=\sqrt{\int^{\infty}_0({\tau-\overline{\tau})^2 \centerdot \frac{1}{\overline{\tau}}e^{-\frac{\tau}{\overline{\tau}}} d \tau}} = \tau\)
则可知对于指数分布的PDP，均方根时延扩展与平均附加时延数值上相等。

5.3.1.2相干带宽

• 在一定范围内频率的统计测量值。在此范围内，两个频率分量具有很强的幅度相关性
• 是从均方根延迟扩展得到的信道频率特性
• 所有通过信道相干带宽的频谱分量均以几乎相同的增益及线性相位通过，即平坦衰落
  计算方法：
• 频率相关系数大于一定门限（\(\rho\)）的特定带宽值
  \(\rho=0.9, B_C \approx \frac{1}{50\sigma_{\tau}}\)，若\(\rho=0.5, B_C \approx \frac{1}{5\sigma_{\tau}}\)

5.3.2多普勒扩展\(B_D\)和相干时间\(T_C\)

时延扩展和相干带宽是用于描述本地信道色散特性的两个参数，而多普勒扩展和相干时间体现由于相对运动引起的信道时变特性。
多普勒扩展\(B_D\)定义为一个一个多普勒频谱非0值的频谱范围

\[B_D \in [f_c-f_d,f_c+f_d] \]

其中\(f_c是信号载频，f_d为多普勒偏移\)

• 相干时间是多普勒扩展在时域的表现，用于描述信道的时变特性,典型取值为

\[T_C \approx \frac{1}{f^{max}_d}, \frac{9}{16\pi f^{max}_d}或\sqrt{\frac{9}{16\pi (f^{max}_d)^2}}=\frac{0.423}{f^{max}_d} \]

到达时间间隔超过\(T_C\)的两个信号受到信道的影响不同。

5.4小尺度衰落类型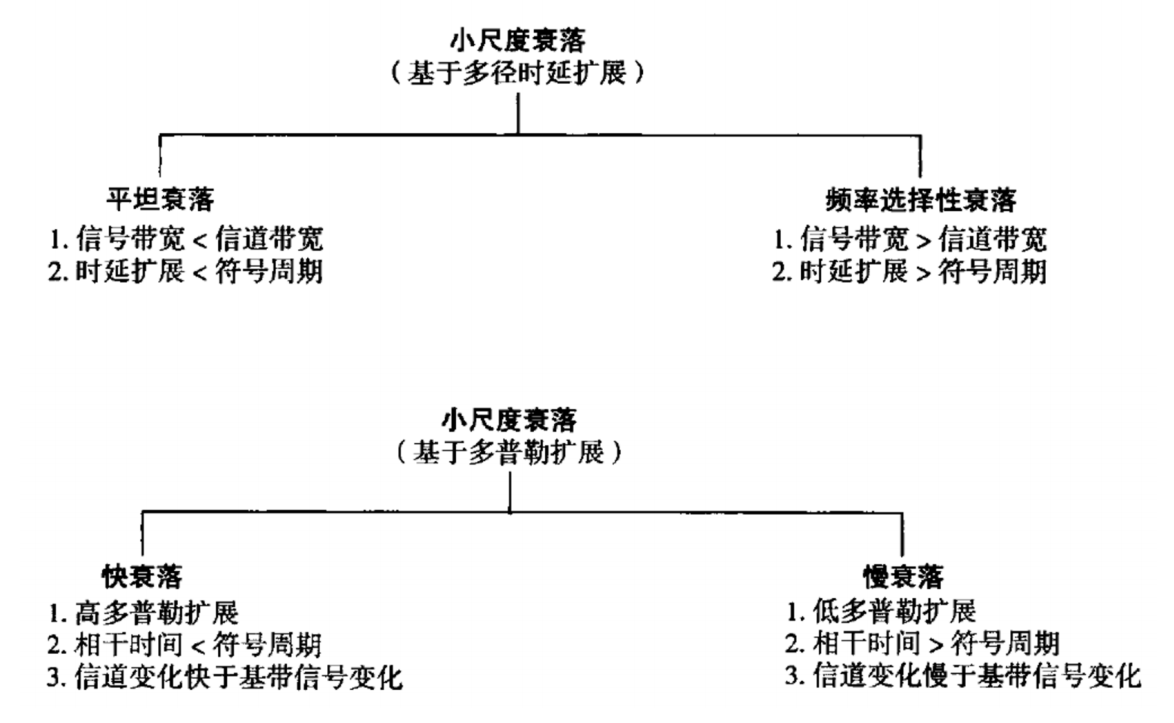 $T_S$:传输模型带宽的倒数（如信号周期）$B_S$:传输模型带宽

\(\sigma_{\tau}\):信道的rms时延扩展 \(B_C\):信道的相干带宽

\(B_D\):信道多普勒扩展带宽 \(T_C\):信道相干时间

5.4.1多径时延扩展引起的衰落效应

• 平坦衰落

\[B_S \ll B_C 即 T_S \gg \sigma_{\tau} \]

• 频率选择性衰落

\[B_S > B_C 即 T_S < \sigma_{\tau} \]

通常若\(T_S \geq 10\sigma_{\tau}\),该信道是平坦衰落的；
若\(T_S < 10\sigma_{\tau}\)，则为频率选择性衰落

5.4.2多普勒扩展引起的衰落效应

• 快衰落

\[T_S > T_C 即 B_S < B_D \]

• 慢衰落

\[T_S \ll T_C 即 B_S \gg B_D \]

显然，移动台的速度以及基带信号的发送速率决定了信号是经历快衰落还是慢衰落。

小尺度衰落模型

5.5基于多径信道的窄带通信 5.5.1瑞利衰落分布

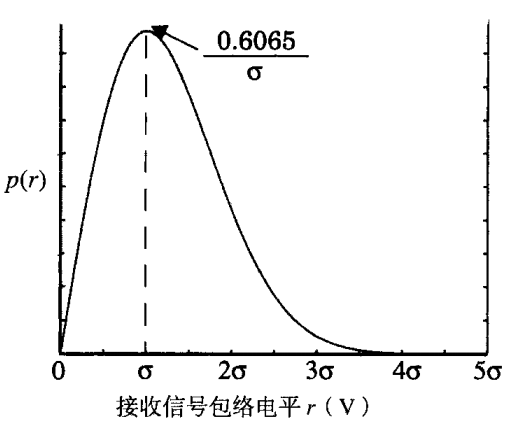
移动无线通信中，瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接收包络统计时变特性的一种分布模型。
两个正交高斯噪声信号之和的包络服从瑞利分布。
概率密度函数pdf:
\(f_R(r)= \begin{cases} \frac{r}{{\sigma}^2} e^{-\frac{r^2}{2{\sigma}^2}} & 0\leq r<\infty \\ 0 & r<0 \end{cases} \)
其中\(\sigma\)是包络检波之前所接收电压信号的均方根(rms)值，\({\sigma}^2\)是包络检波之前接收信号包络的时间平均功率。

信道的平均增益：\(\overline{r^2}=2{\sigma}^2\)
中断率（outage probability）
\(Pr(r \leq r_{min})=\int^{r_{min}}_{-\infty}{f_R(r)dr}=\int^{r_{min}}_0{\frac{r}{{\sigma}^2} e^{-\frac{r^2}{2{\sigma}^2}}dr} = 1-e^{-\frac{r^2_{min}}{2{\sigma}^2}}\)

• 令\(P=r^2\)为信号功率，则有\(r=\sqrt{P}\)

\[f_P(P)=\frac{\sqrt{P}}{{\sigma}^2} e^{-\frac{P}{2{\sigma}^2}}det(J_r) \]

\[=\frac{\sqrt{P}}{{\sigma}^2} e^{-\frac{P}{2{\sigma}^2}}\centerdot \frac{1}{2\sqrt{P}}=\frac{1}{\overline{P}}e^{-\frac{P}{\overline{P}}} \]

• \(Pr(r \leq R)=1-e^{-\frac{R^2}{2{\sigma}^2}}\)
  其中\(\overline{P}\)是基于瑞利信道的平均接收功率（也就是\(\overline{P}=2{\sigma}^2\)）

若 \(\rho = \frac{R}{\sqrt{2}\sigma}\)

则有\(Pr(r \leq R) = 1-e^{-\rho^2}\)

• notice
  \(\rho\)幅值之比，换算dB要是20log()；对于功率是10log()

在瑞利信道中，接收信号功率（信道增益）服从指数分布；
故而，基于接收功率计算中断率有：

\[Pr(P_r<P_{min})=cdf(P_{min})=1-e^{\frac{P_{min}}{\overline{P}}} \]

(以上计算均是线性单位)
hh

5.5.1.1 瑞利信道：衰落余量

为了保证不超过x的中断率

\[Pr(P_r<P_{min})=1-e^{\frac{P_{min}}{\overline{P}}}<x \]

\[\frac{P_{min}}{\overline{P}}<ln\frac{1}{1-x} \Rightarrow FM = \frac{\overline{P}}{P_{min}}>\frac{1}{ln\frac{1}{1-x}} \]

\(\frac{1}{ln\frac{1}{1-x}}\)即为中断率为x的衰落余量[单位线性]
当x足够小时，有\(FM \geq \frac{1-x}{x} \approx \frac{1}{x}\)

• 当同时考虑大尺度和小尺度衰落时，总衰落余量有

\[M[dB] = M_{shadowing}[dB]+M_{Rayleigh}[dB] \]

5.5.2 LOS传输：莱斯信道

当信道中存在一个固定的直射分量时，接收信号是复高斯分量和直射分量的叠加，包络服从莱斯分布。
也就是Rayleigh加了一个视距分量

• 莱斯系数K

\[K=\frac{A^2}{2{\sigma}^2} \]

其中