 高等数学总复习 考研基础课
高等数学总复习
杂项
1. 三角不等式
\[||x| - |y|| \leq |x\pm y| \leq |x| + |y|
\]2. \((ln|x|)' = \frac{1}{x}\)
3.极限的一个结论
\[\lim_{n \to \infty} \sqrt[n]{a^n+b^n+c^n} = max (a, b, c)\\ (a, b, c > 0)
\]\[\lim_{n \to \infty} \sqrt[n]{x^n+x^n+...+x^{n^2}} = max (x, x^2, ...,x^{n^2})\\ (x > 0)
\]4. 初等函数在定义区间内连续
高等数学总复习 考研基础课
高等数学总复习
杂项
1. 三角不等式
\[||x| - |y|| \leq |x\pm y| \leq |x| + |y|
\]2. \((ln|x|)' = \frac{1}{x}\)
3.极限的一个结论
\[\lim_{n \to \infty} \sqrt[n]{a^n+b^n+c^n} = max (a, b, c)\\ (a, b, c > 0)
\]\[\lim_{n \to \infty} \sqrt[n]{x^n+x^n+...+x^{n^2}} = max (x, x^2, ...,x^{n^2})\\ (x > 0)
\]4. 初等函数在定义区间内连续
连续函数加减乘除、复合 ——> 结果还是连续
5. $当x\in (0, \pi/2)时,tanx > x > sinx $ 6.伽马函数:\(\int_0^{+\infty}x^ne^{-x}dx=n!(n\in N^+)\) 一、极限 0. 求极限总论: 处理准则:-
定型:若为已定式,直接代入求解;若为未定式,见2;
-
四化:
- 非0代入
- 根式化简
- 无穷小 \(\to\) 泰勒,洛必达,四则运算
- 幂指函数
-
必须要分左右极限来求的情况:
\[e^\infty,1^\infty ;\,\,arctan\infty;\,\, [x](x\to Z) ;\,\,|x|;\,\,分段函数 \]
不可局部代值,除非是非零因子
1. 按照考点划分 (0)重要极限 \[\lim_ {n \to \infty} \sqrt[n]{n} = 1,\lim_{n \to \infty}\sqrt[n]{a} = 1\\ \lim_{x\rightarrow \infty}(1+\frac1x)^x=e\\ \](1) 无穷小量 常见等价无穷小替换- \(x+\alpha(x) \backsim x\)
- \[\lim_{n \to \fbox{} }f(x) = a\Leftrightarrow f(x)=a+\alpha\\ (\alpha 是x \to \fbox{}时的无穷小) \]
- \(lnf(x),(f(x)\rightarrow1)\)型:\(lnf(x)=ln[1+f(x)-1]\backsim f(x)-1\)
- \(f^{\alpha}(x)-1,(f(x)\rightarrow1)\)型:\([f(x)-1+1]^{\alpha}-1\backsim \alpha[f(x)-1]\)
展开原则:相消不为0且上下同阶
\(x\rightarrow 0\)
\[sinx=x-\frac1{3!}x^3+\frac1{5!}x^5+o(x^5)\\ arcsinx=x+\frac1{3!}x^3+o(x^3)\\ cosx=1-\frac1{2!}x^2+\frac1{4!}x^4+o(x^4)\\ tanx=x+\frac13x^3+o(x^3)\\ arctanx=x-\frac13x^3+\frac15x^5+o(x^7)\\ e^x=1+x+\frac1{2!}x^2+\frac1{3!}x^3+o(x^3)\\ ln(1+x)=x-\frac12x^2+\frac13x^3\\ (1+x)^\alpha=1+\alpha x+\frac{\alpha (\alpha-1)}{2!}x^2+o(x^2) \]常用:
\[x-sinx \backsim \frac16x^3\\ x-arcsinx \backsim -\frac16x^3\\ x-tanx \backsim -\frac13x^3\\ x-arctanx \backsim \frac13x^3\\ x-ln(1+x)\backsim \frac12x^2\\ Tips:碰到cosx\pm 1,利用cos2x=2cos^2x-1消掉 \](3)洛必达- 注意使用条件。洛完结果不唯一就不能洛
- 乘除法中的非0项可以先算
- \(e^f-e^g\)型:提后者
-
定义
\[\lim_{n \to \infty}x_n = A\Leftrightarrow \forall \sigma > 0, |x_n-A|<E\\(\exist N > 0, 当n>N时) \] -
延伸
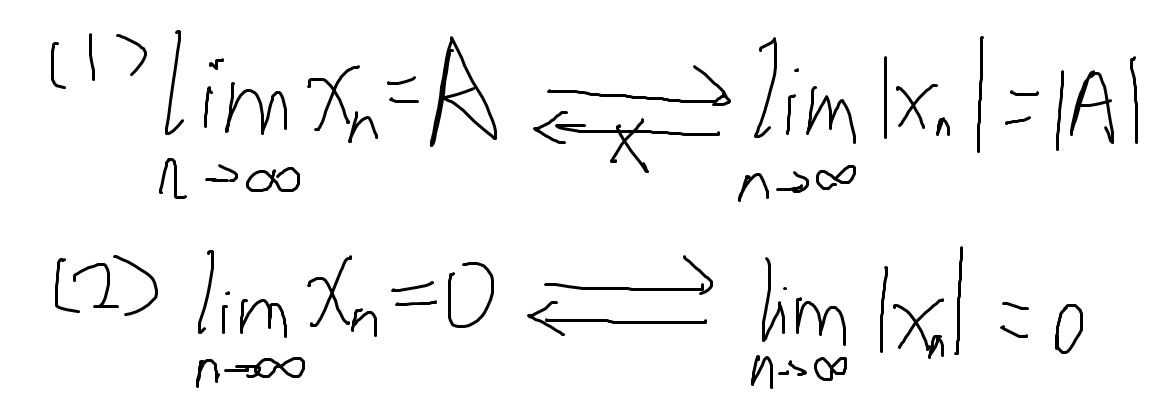
-
收敛 / 发散
\[\lim_{n \to \infty}x_n= \begin{cases} A\exists \Rightarrow \{x_n\}收敛于A\\ A不\exists \Rightarrow \{x_n\}发散 \end{cases} \] -
极限含义
存在N,其后所有数都接近A
-
收敛一定有界,有界不一定收敛
-
保号性:(要注意是后面才保号,前面无关)
\[若\lim_{n \to \infty}x_n>0,则n \to \infty时,x_n>0 \]
-
大前提
-
不可导(不连续)
-
不能往0跑
-
-
- 转化为函数(连续化处理)
-
-
夹逼准则
\[z_n \leq x_n \leq y_n\\ 同一趋向时,z_n和y_n极限相同 \]常用放缩方法:
-
分子分母同阶时,放缩分母使得分子可加
- \[A_1,A_2,...,A_n>0且M = max(A_1,A_2,...,A_n)时,\\M \leq A_1+A_2+...+A_n \leq nM \]
-
-
-
3.数列极限求和形式
- 利用不定积分的计算型定义
-
原理:单调有界必有极限, 方法:数学归纳法
-
在草稿纸上求出极限
-
验证 n = 1时成立
-
假设n = k时成立,证明n = k +1时也成立
-
证毕
-
-
- 等价无穷小替换
-
- 洛必达
-
- 复杂函数用 泰勒公式 / 麦克劳林替换
- 抓大头;上下同除最大项;洛必达
-
有分母:通分
-
无分母:分子有理化,倒代换
-
转化为 \(\frac{0}{0}\) 或者 \(\frac{\infty}{\infty}\)
-
注:不要把 $$ln$$ 或 反三角 放分母
- \(lim u ^ v = e ^{lim v (u-1)},(u \to 1,v \to \infty)\)
-
用对数恒等式,把指数放下来
-
不要忘了 e !!!
- 由部分推整体
- 与等差等比,定积分等结合
- 洛必达
- 积分中值定理
- 放缩然后夹逼 (比较定理)
-
瞬时变化率
\[f'(x_0)= \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \] -
增量定义
\[\lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \] -
重要
\[f'(x_0)=\lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0} \]
- \[f'_+(x_0)=\lim_{x \to x_0^+}\frac{f(x)-f(x_0)}{x-x_0}\\ f'_-(x_0)=\lim_{x \to x_0^-}\frac{f(x)-f(x_0)}{x-x_0} \]
-
重要性质:不可导的绝对值函数\(|x-x_0|\)乘上可导(连续)函数之后变可导
-
常见易错
\(f(x)\) 在 \(x_0\)处可导,则\(f'(x)在x_0\)处连续 (错!,应该为\(f(x)在x_0\)处连续)
若\(f''(x_0)\exists\),则\(f'(x)在x_0\)处连续 √
若\(f''(x_0)\exists\),则\(f(x)在x_0\)处连续 √
-
分段函数
分段点上用定义求
-
一阶
\[\frac{dx}{dy}=\frac{1}{f'(x)} \] -
二阶
\[\frac{d^2x}{dy^2}=-\frac{f''(x)}{[f'(x)]^3} \]
-
公式法(5条 + 莱布尼茨)
\[1. [\frac1{ax+b}]^{(n)}=\frac{a^nn!(-1^n)}{(ax+b)^{n+1}}\\ 2. [a^x]^{(n)}=a^x(lna)^n,\,\,[e^{ax}]^{(n)}=e^{ax}a^n\\ 3. [sinx]^{(n)}=sin(x+\frac n2\pi),\,\,[cosx]^{(n)}=cos(x+\frac n2\pi)\\ 4. [x^\alpha]^{(n)}= \begin{cases} 0, & n>\alpha\\ \alpha(\alpha-1)...(\alpha-n+1)x^{\alpha-n} & n\leq \alpha \end{cases}\\ 5.莱布尼茨:[AB]^{(n)}=C_n^0A^{(n)}B+C_n^1{A^{(n-1)}}B^1+...+C_n^nAB^{(n)} \] -
泰勒展开
-
递归法
-
切方 (k为该点导数),法方 (垂直于切方)
-
极坐标与参数方程互化
\[x=r(\theta)cos\theta,\,\,y=r(\theta)sin\theta\\ r(\theta)=\sqrt{x^2+y^2} \] -
相切:\(f(x_0)=g(x_0)且f'(x_0)=g'(x_0)\)
-
辨析:\(自变量:\Delta x=dx; 因变量:\Delta y \neq dy\)
-
\(y=f(x),若满足 \Delta y=A\Delta x+O(\Delta x),\Delta x\to 0,则y=f(x)可微\)
其中,\(A\)就是微分\(dy\),也叫线性主部
- 切线增量\(dy\)(直线),函数增量\(\Delta y\)(曲线) (\(\Delta x \to 0,\Delta y \approx dy\))
-
规范答案书写
除拐点要写点坐标之外,间断点、极值点、极值、驻点等都填值
-
单调性
一点导数正负性不决定邻域内单调性,除非导数连续
-
单调性误区
单点\(f'(x_0)\)不能证明增减
- 若\(f'(x_0)>0\),无法判断\(f(x)\)在\(x_0\)邻域内的单调性
- 若\(f'(x_0)>0\)且\(f'(x_0)\)在\(x_0\)处连续,则断\(f(x)\)在\(x_0\)邻域内单增
-
单调性的破题方法
\(F'(x)\rightarrow F''(x)\rightarrow F'''(x)\rightarrow ...\) : 找上一级为0的点
- 6种常见构造方法
-
-
函数极值
-
定义:邻域(左右都有)
-
可疑点:1. 驻点\(f'(x_0)=0\) 2. \(f'(x_0)\)不存在
-
第一充分条件:若\(f(x)\)在\(x_0\)处连续,且\(f'(x)\)在\(x_0\)去心邻域两侧异号
-
第二充分条件:若\(f'(x_0)=0\)且\(f'(x_0)\neq 0\) (\(>0\)取极小,\(<0\)取极大)
-
-
函数最值
- 连续的函数中,唯一极值点就是最值点
- 求解步骤:1. 求(a, b)内极值 2. 求f(a) f(b) 3. 比较
-
函数凹凸性
-
判定:$\forall x \in I,f''(x)>0\rightarrow \(凸;\)\forall x \in I,f''(x)<0\rightarrow $凹
-
定义:(凹函数)割线高于曲线;(凸函数)割线低于曲线
-
拐点
-
定义:凹凸线发生改变的点
-
可疑点:1. \(f''(x_0)=0\) 2. \(f''(x_0)\)不存在
-
第一充分条件:\(f''(x_0)\)两侧异号
-
第二充分条件:\(f''(x_0)=0\)且\(f'''(x_0)\neq 0\)
-
-
-
求渐近线(先垂直后水平最后斜)
-
垂直:1. 找无定义点\(x_0\) 2. \(\lim_{x\rightarrow x_0}{f(x)}=\infty\)
-
水平:\(\lim_{x\rightarrow \infty}{f(x)}=A\) \((x\rightarrow +\infty / -\infty)\)相同拆开,不同合并
-
斜:
\[a=\lim_{x\rightarrow \infty}{\frac{f(x)}{x}}, b=\lim_{x\rightarrow \infty}[f(x)-ax] \]
-
-
曲率圆
-
曲率半径\(R\),曲率\(k=\frac{1}{R}, k\)越大, 越弯
- \[k=\frac{|y''|}{[1+y'^2]^{\frac {3}{2}}},且k>0 \]
-
- 凑即积
若\(\int f(x)dx\)存在:
- \(f(x)\)连续,则原函数必存在
- \(f(x)\)存在第一类 / 无穷间断点。则原函数必不存在
- 若\(f(x)\)有振荡间断点,则原函数可能存在
别漏了绝对值
\[\int tanxdx=-ln|cosx|+C\\ \int cotxdx=ln|sinx|+C\\ \int secxdx=ln|secx+tanx|+C\\ \int cscxdx=ln|cscx-cotx|+C\\ \int sec^2xdx=tanx+C\\ \int csc^2xdx=-cotx+C\\ \int secxtanxdx=secx+C\\ \int cscxcotxdx=-cscx+C\\ \]\[\int \frac1{x^2+a^2}dx=\frac1aarctan\frac xa+C\\ \int \frac1{x^2-a^2}dx=\frac1{2a}ln|\frac{x - a}{x+a}|+C\\ \int \frac1{\sqrt{a^2-x^2}}dx=arcsinx\frac xa+C\\ \int \frac1{\sqrt{a^2+x^2}}dx=ln(x+\sqrt{x^2+a^2})+C\\ \int \frac1{\sqrt{x^2-a^2}}dx=ln|x+\sqrt{x^2-a^2}|+C\\ \int \frac1{a^2sin^2x+b^2cos^2x}dx\rightarrow\frac1{ab}arctan\frac{atanx}b+C(同除cos^2x)\\ \int \frac{asinx+bcosx}{dsinx+ecosx}dx\rightarrow \int \frac{m分母+n分母'}{分母}dx(配系数) \](2)ex 类凑一个\(e^x\)以便凑微分
\[eg.\int \frac1{1+e^x}dx=\int \frac{1+e^x-e^x}{1+e^x}dx=x-ln(1+e^x)+C \](3)三角函数类-
模型题
-
必备转化公式
\[tan^2x+1=sec^2x,\,\,\,cot^2x+1=csc^2x \] -
1碰cos,消
\[1+cosx=2cos^2\frac x2,\,\,\,cosx-1=-2sin^2\frac x2 \] -
次数:偶次降幂,奇次凑分(拿出一个)
-
注:d x 也要换,别忘了代回
-
三角代换
-
\[\sqrt{a^2-x^2}\rightarrow 令x=asint\\
\sqrt{a^2+x^2}\rightarrow 令x=atant\\
\sqrt{x^2-a^2}\rightarrow 令x=asect\\
\]
换回方法:画一个三角形,用a x 表示三条边
-
无理根式换元
\[直接令t=\sqrt[n]{ax+b}或\sqrt[n]{\frac{ax+b}{cx+d}} \]
-
规则:反对幂三指(谁在后谁入d)
-
技巧:乘法公式逆用
直接配的两类:
- \(\int\frac1{Ax^2+Bx+D}dx\) 配方,化成 \(\frac1{x^2+a^2}\)
- \(\int\frac{Ex+F}{Ax^2+Bx+D}dx\) 配凑:\(\int \frac{m分母'+n'}{分母}dx\)
-
假分式化真分式
-
拆分(分母必须要化简到最简形式再拆分)
-
括号外决定项数
-
分子写比分母低一次的多项式
-
有括号(比括号低一次)
-
无括号(比分母低一次)
-
-
括号内看次方项
-
面积:
\[\lim_{n\rightarrow \infty}\sum_{i=1}^{n}\frac{b-a}nf(a+\frac{b-a}ni)=\int_a^bf(x)dx \](2)基本形式 \[1. \lim_{n\rightarrow \infty}\frac1n\sum_{i=1}^{n}f(\frac in)=\int_0^1f(x)dx(右端点)\\ 2.\lim_{n\rightarrow \infty}\frac1n\sum_{i=1}^nf(\frac{i-1}n)=\int_0^1f(x)dx(左端点) \]-
可用于数列极限求和:1. 和 2. 提 3. 找项
-
拓展:分为\(2n\)份(\(n\rightarrow 2n\))
椭圆(两点定直径):
\[x^2+y^2=ax过(0,0)和(a,0)\\ x^2+y^2=bx过(0,0)和(0,b) \]3. 定积分性质 (1)基本定积分是一个数,与变量选取无关
(2)奇偶性 \[奇函数:\int_{-a}^af(x)dx=0\\ 偶函数:\int_{-a}^af(x)dx=2\int_0^af(x)dx \](3)比较定理积分线相同,被积函数不同,考比较定理
- 若\(f(x\leq g(x))\)则\(\int_a^bf(x)dx\leq \int_a^bg(x)dx,(b>a)\)
- 只要有一个部分比你大,绝对比你大
- 仅需比较两个被积分函数的大小
-
\(\int_0^{nT}f(x)dx=n\int_0^Tf(x)dx\)
-
\(\int_a^{a+T}f(x)dx\)与\(u\)无关(只要积分线长度等于周期,就都相等)
若\(f(x)\)在\([a,b]\)连续,则至少存在一个\(\xi \in [a,b]\)使\(\int_a^bf(x)dx=f(\xi)(b-a)\)
平均值:\(\overline{f(x)}=\frac{\int_a^bf(x)dx}{b-a}\)
只要积分变量字母不变,上下限范围所属关系不变
4. 求定积分 (1)华莱士公式(点火公式) \[\int_0^{\frac\pi2}sin^nxdx=\int_0^\frac\pi2cos^nxdx= \begin{cases} \frac{n-1}n\frac{n-3}{n-2}...\frac12\frac\pi2,&n为偶\\ \frac{n-1}n\frac{n-3}{n-2}...\frac23,&n为奇 \end{cases} \]\[1. \int_0^{\frac\pi2}sin^nxdx=\int_0^{\frac\pi2}cos^nxdx\\ 2. \int_0^\pi sin^nxdx=2\int_0^\frac\pi2sin^nxdx\\ 3. \int_0^\pi cos^nxdx= \begin{cases} 2\int_0^{\frac\pi2}cos^nxdx,&n为偶\\ 0,&n为奇\\ \end{cases}\\ 4.\int_0^{2\pi}sin^nxdx=\int_0^{2\pi}cos^nxdx= \begin{cases} 4\int_0^{\frac\pi2}sin^nxdx,&n为偶\\\ 0,&n为奇 \end{cases} \](2)第二类换元积分法-
基本原则:三换(换被积函数,换积分变量,换上下限)
-
轮换对称性:\(\int_0^{\frac\pi2}f(sinx,cosx)dx=\int_0^{\frac\pi2}f(cosx,sinx)dx\) (证明:令\(\frac\pi2-x=t\))
-
区间再现换元法: 令“上+下 – x = t ”
\[eg.\int_a^bf(x)dx,令b+a-x=t\\ 则\int_a^bf(x)dx=-\int_b^af(b+a-t)dt=\int_a^bf(b+a-x)dx \]来两个典例:
\[1.\int_0^\pi xf(sinx)dx=\frac\pi2\int_0^\pi f(sinx)dx, \,\,\,\,\,2.求\int_0^\pi \frac{xsinx}{1+cos^2x}dx \]
\(F(x)=\int_a^xf(t)dt:\) \(x\) 是自变量,\(t\)是积分变量
(1)定理- 若\(f(x)\)连续,且\(F(x)=\int+a^xf(t)dx\),则\(F(x)\)必可导,且\(F'(x)=f(x)\),则\(F(x)\)为\(f(x)\)的一个原函数
- 若\(f(x)\)连续,则\(\int f(x)dx=\int_0^xf(t)dt+C\)
-
标准型:若\(f(x)\)连续,\(F(x)=\int_{\alpha(x)}^{\beta(x)}f(t)dt\)
则 \(F'(x)=f[\beta(x)]\beta'(x)-f[\alpha(x)]\alpha'(x)\)(上进上导—下进下导)
-
非标准型:换元,把x当作常量
\[令x-t=u,则\int_0^xf(x-t)dt=\int_x^0f(u)d(x-u)=-\int_x^0f(u)du=\int_0^xf(u)du \]
有一端为\(\infty\) 或 存在瑕点(无定义点 且 该点极限为\(\infty\))
(2)计算- 先找瑕点(奇点)(有瑕点一定要拆开来算)
- \(\infty\)型:正常算 \(+\, lim\, \infty\)
- 四则运算
- 伽马函数
- 无穷区间的反常积分\(\int_1^{+\infty}\frac{dx}{x^p}:\) 在\(p>1\)时收敛,在\(p\leq1\)时发散
- 无界函数的反常积分\(\int_0^1\frac{dx}{x^p}(p>0,奇点x=0):\) 在\(0<p<1\)时收敛,在\(p\geq 1\)时发散
-
变力做功问题:\(W=\int_a^bF(x)dx\)
-
水下压强:\(F_压=\int_0^b\rho gax\,dx\)
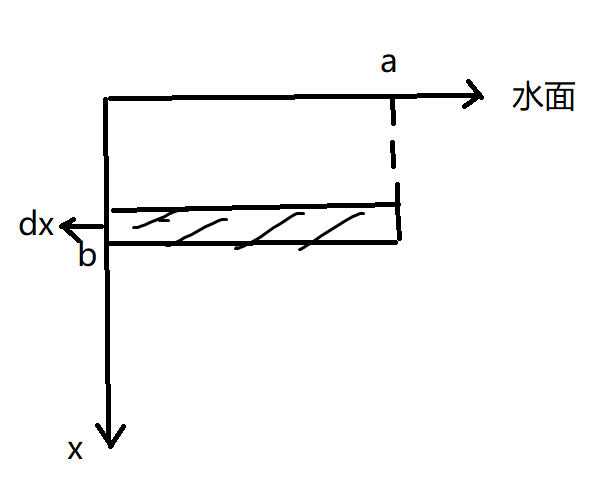
这图画了老半天
-
定义
-
极直转换:\(x=rcos\theta,\,\,y=rsin\theta\)
-
常见平面极坐标曲线
- 心形线
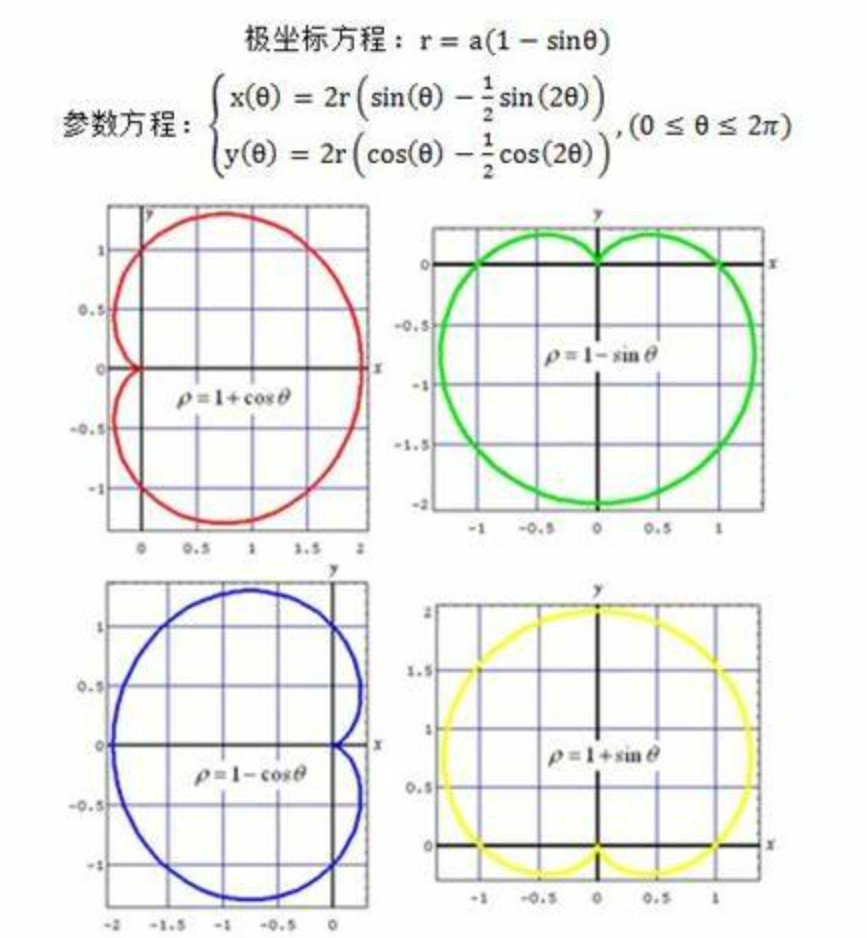
-
双扭线:\((x^2+y^2)^2=a^2(x^2-y^2)\)
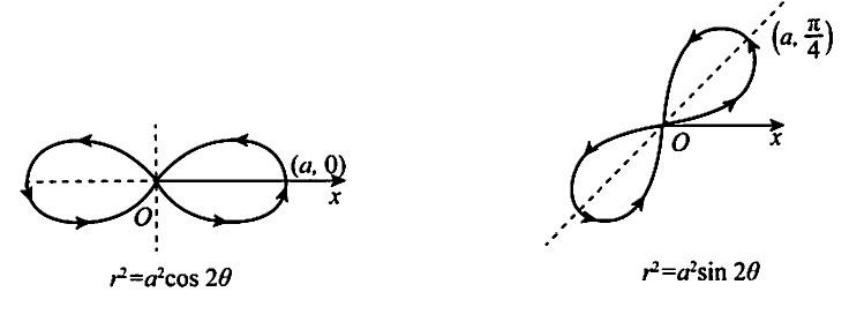
-
阿基米德螺线
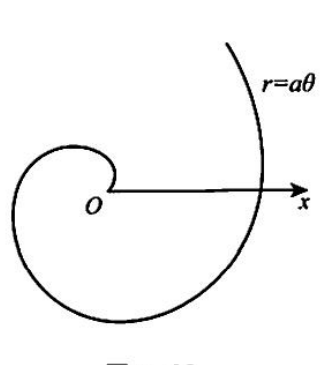
-
玫瑰线
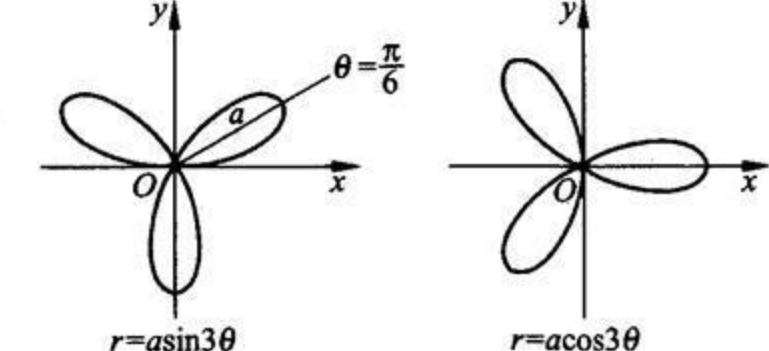
- 面积\[S_1=\int_a^b[y_2(x)-y_1(x)]dx,\,\,\,\,S_2=\int_c^d[x_2(y)-x_1(y)]dx \]注:靠近正半轴的 – 远离正半轴的
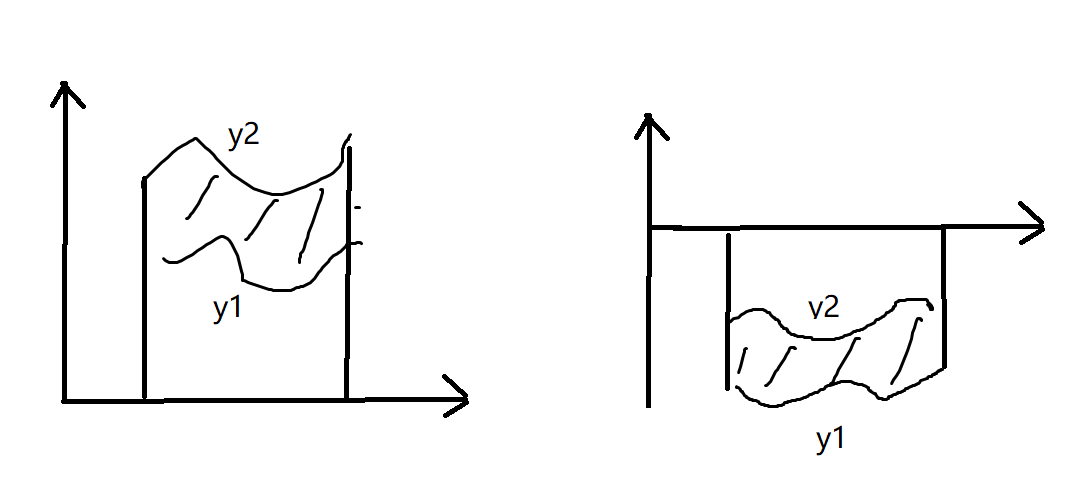
-
极坐标
-
参数方程

-
x 轴
-
y 轴
-
x = c

- 弧微分
-
概念
c 的个数就是阶数
-
一阶微分方程判定思路
\[\frac{dy}{dx}=...\rightarrow 可分离f(x)g(x)\rightarrow 齐次f(\frac yx)\rightarrow \\头重脚轻(如果不是,就先倒代换再做) \begin{cases} 1. 一节非齐次线性方程\\ 2. 伯努利 \end{cases} \]
齐次:\(c_1\)齐 + \(c_2\)齐 (\(c_1,c_2\)线性无关)
非齐次:\(c_1\)齐 + \(c_2\)齐 + 非齐次线性方程组的一个特解
转化:非齐次作差 \(\rightarrow\) 齐次
3. 一阶 (1)可分离 \[\frac{dy}{dx}=f(x)g(x) \]出现\(ln:+ lnc_1\) (以便化简)
(2)齐次 \[\frac{dy}{dx}=f(\frac yx)\rightarrow 令\frac yx = u,\,\,则\frac{dy}{dx}=u+x\frac{du}{dx} \](3)一阶非齐次线性形式:\(y'+p(x)y=q(x)\)
公式:
\[y=e^{-\int p(x)dx}[\int q(x)e^{\int f(x)dx}dx+c] \](注:不必加绝对值)
助记(积分因子法):
-
先找到因子\(e^{\int p(x)dx}\),原方程两边同乘该因子,得
\[y'e^{\int p(x)dx}+y\,p(x)e^{\int p(x)dx}=q(x)e^{\int p(x)dx} \] -
观察易得,左半边为 \([y\,e^{\int p(x)dx}]'\)
-
两边同时积分就能解得 \(y\)
形式:\(y'+p(x)y=q(x)y^n\)
做法:
-
一除:\(\frac 1{y^n}y+p(x)y^{1-n}=q(x)\)
-
二换:令\(z=y^{1-n}\),则\(\frac{dz}{dx}=\frac{dz}{dy}\cdot \frac{dy}{dx}=(1-n)y^{-n}\frac{dy}{dx}\)
-
三回代:\(\frac 1{1-n}\frac{dz}{dx}+p(x)z=q(x)\)
最后化为一阶非齐次线性:\(\frac{dz}{dx}+(1-n)p(x)z=(1-n)q(x)\)
- 不显 \(y,\,y''=f(y',x):\) 令 \(y'=p,\) 则\(y''=\frac{dp}{dx}\)
- 不显 \(x,\,y''=f(y',y):\) 令 \(y'=p,\) 则\(y''=p\frac{dp}{dy}\)
-
齐次
-
写特征方程:\(\lambda^2+p\lambda+q=0\)
-
解特征值:\(\lambda_1,\lambda_2\)
-
写通解
\[\begin{cases} \lambda_1\neq\lambda_2\rightarrow c_1e^{\lambda_1x}+c_2e^{\lambda_2x}\\ \lambda_1=\lambda_2\rightarrow (c_1+c_2x)e^{\lambda_1x}\\ \lambda_{1,2}=\alpha\pm\beta i\rightarrow e^{\alpha x}[c_1cos\beta x+c_2sin\beta x] \end{cases} \]
-
-
非齐次
- 存在一个\(\xi\)使得等式成立
- $F(\xi)=0\rightarrow \(**零点定理**\)\rightarrow F(x)$
- $F'(\xi)=0\rightarrow \(**罗尔定理**\)\rightarrow $三步构造
- 证\(f(\xi)=A\rightarrow\)介值定理+最值定理\(\rightarrow m\leq A \leq M\)
- 同一函数做差\(\rightarrow\)拉格朗日中值定理
- 两个不同函数做差\(\rightarrow\)柯西中值定理
\(m, M\)
(3)介值定理若\(f(x)\)在\([a,b]\)连续,且\(m<A<M\),则至少 \(\exists \,\xi\in[a,b]\)。使\(f(\xi)=A\)
\[平均数:f(\xi)=\frac{c_1f(x_1)+c_2f(x_2)+...+c_nf(x_n)}{c_1+c_2+...+c_n}\\ f(\xi)=\frac{f(x_1)+f(x_2)+...+f(x_n)}{x_1+x_2+...+x_n},\,\,\xi \in [x_1,x_n] \](4)零点定理若\(f(x)\)在\([a,b]\)连续,且\(f(a)f(b)<0\),则至少 \(\exists \,\xi\in a,b\),使\(f(\xi)=0\)
3. 积分中值定理去积分线
(1)使用若\(f(x)\)在\([a,b]\)连续,则至少 \(\exists \,\xi\in [a,b]\),使\(\int_a^bf(x)dx=f(\xi)(b-a)\)
\[平均数:\overline{f(x)}=\frac {\int_a^bf(xdx)}{b-a} \](2)证明 \[证明f(\xi)=\frac{\int_a^bf(x)dx}{b-a}:\\ f(x)在[a,b]连续,则m\leq f(x)\leq M\\ \therefore \int_a^bmdx\leq\int_a^bf(x)dx\leq \int_a^bMdx\\ \therefore m(b-a)\leq f(b)-f(a)\leq M(b-a)\\ \therefore m\leq \frac{f(b)-f(a)}{b-a}\leq M\\ 由介值定理得,必定\exists \,\xi \in[a,b],使得f(\xi)=\frac{1}{b-a}\int_a^bf(x)dx\\ \therefore \int_a^bf(x)dx=f(\xi)(b-a) \](3)广义积分中值定理可使用拉格朗日中值定理推广至\((a,b)\):
若\(f(x)\)在\((a,b)\)连续,则至少 \(\exists \,\xi\in [a,b]\),使\(\int_a^bf(x)dx=f(\xi)(b-a)\)
原理:被积分函数连续,变限函数一定可导
若\(f(x)\)在\(x_0\)处取得极值,且\(f(x)\)在\(x_0\)处可导,则\(f'(x_0)=0\)
(2)罗尔定理若\(f(x)\)在\([a,b]\)连续,\((a,b)\)可导,且\(f(a)=f(b)\),则\(\exists \, \xi \in (a,b),\,f'(\xi)=0\)
找\(F(x)\)的万能法:
- \(\xi \rightarrow x\)
- 找原函数:不定积分 / 微分方程
- \(c = F(x)=...\) (把\(c\)扔一边,另一边就是\(F(x)\)
用罗尔定理证得
\[若f(x)在[a,b]连续,(a,b)可导,则\frac{f(b)-f(a)}{b-a}=f'(\xi) \](4)柯西中值定理 \[若f(x)在[a,b]连续,(a,b)可导,且g'(x)\neq 0,\\则\exists \,\xi\in (a,b),使得\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi)}{g'(\xi)},\,\,(a<\xi < b) \]证明:
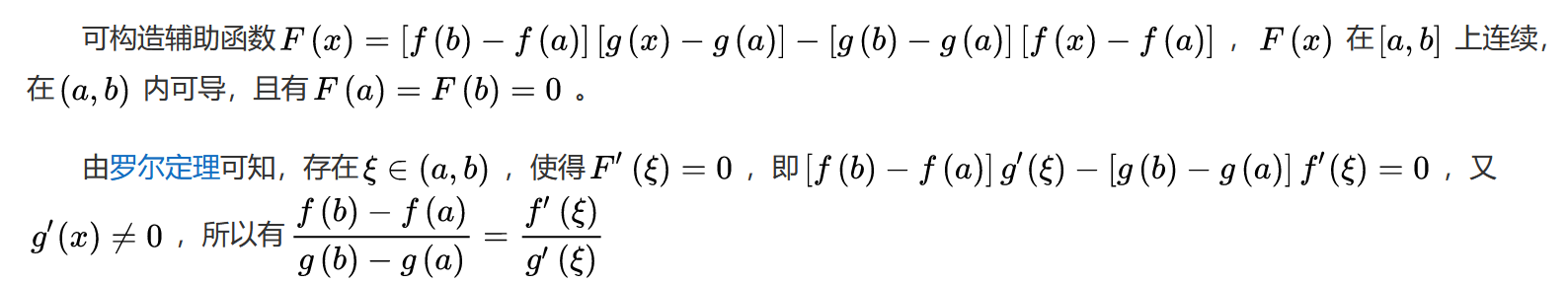
特别的,当\(x_0=0\)时有麦克劳林公式:
\[1. f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+...+\frac{f^{(n)}(0)}{n!}x^n+o(x^n)\\ 2. f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+...+\frac{f^{(n)}(0)}{n!}x^n+\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} \]七、多元函数微分学 八、多元函数积分学 1. 概念 (1)含义绝对体积
\[V = \lim_{n \to \infty}{\sum_{i=1}^nf(\xi_i,\eta_i)\Delta \sigma_i} = \int_ {} \int_D f(x, y)\, d\sigma \]积分变量\(d\sigma = dx\, dy\)
取点 \(\rightarrow\) 划线 \(\rightarrow\) 投影 \(\rightarrow\) 积分
(2)性质 \[\int_ {} \int_D 1\, d\sigma = S_D \](3)比较定理积分线相同,函数不同
若在 D 上\(f(x, y) \leq g(x, y)\) 则有
\[\int_ {} \int_D f(x, y)\, d\sigma \leq \int_ {} \int_D g(x, y)\, d\sigma \](4)中值定理\(f(x, y)\)在有界闭区域 D 上连续,至少存在一点\((\xi ,\eta) \in D\),使得
\[\int_ {} \int_D f(x, y)\, d\sigma = f(\xi, \eta)\sigma \]2. 计算 (0)综合运用画出积分区域,有对称性就用技巧法,没有就用直接法 (二者结合着用)
拆
分块区域
(1)直角坐标算二重积分-
X 型:先积 x 后积 y
\[\int_a^b {dx}\int_{\phi_1(x)}^{\phi_2(x)}f(x, y)\, dy \] -
Y 型:先积 y 后积 x
\[\int_a^b {dy}\int_{\phi_1(y)}^{\phi_2(y)}f(x, y)\, dx \]
-
适用:积分区域是圆 或 被积分函数是:
\[f(x^2+y^2),f(\frac{ax^n+by^n}{cx^n+dy^n})(同比次方式) \] -
公式:
\[\int_{\alpha}^{\beta} {} \,{\rm d}\theta \int_{0}^{r(\theta)} {f(rcos\theta,rsin\theta)}r\,{\rm d}r \]- 找 \(\theta\) : 范围\([\alpha, \beta]\)
- 取 \(\theta\) : 做射线,找边界方程 \(r(\theta)\)
- 助记 :\(ds = dx\, dy = r \, dr \, d\theta\)
适用抽象函数
a. 积分区域下的奇偶性- 积分区域 D 关于 x 轴对称 \(\rightarrow\) 看 y 函数( y 奇为0, y 偶为2倍)
- 积分区域 D 关于 y 轴对称 \(\rightarrow\) 看 x 函数( x 奇为0, x 偶为2倍)
- 拆解,做辅助线
区域关于 y = x 对称
x y 互换,然后二者加起来
