题意简述
- 有 \(n\) 只奶牛,第 \(i\) 只奶牛希望拜访第 \(a_i\) 只奶牛。
- 给定一个 \(1\) . . . \(N\) 的排列 \((p_1, p_2, ..., p_n)\),对于从 \(1\) 到 \(n\) 的每一个 \(i\):
- 如果奶牛 \(a_{p_i}\) 已经离开了她的农场,那么奶牛 \(p_i\) 仍然留在她的农场。
- 否则,奶牛 \(p_i\) 就会离开她的农场去拜访第 \(a_{p_i}\) 只奶牛,并产生 \(v_{p_i}\) 次快乐的哞叫。
- 给出序列 \(a_n\) 与 \(v_n\),对于所有可能的排列 \(p\),计算可能得到的快乐哞叫的次数的最大值。
- \(2 \leq n \leq 10^5\),\(0 \leq v_i \leq 10^9\)。
解题思路
十分有趣的图论题。
我们建立一个 \(n\) 条边 \(n\) 个点的有向图,第 \(i\) 条边从 \(i\) 连向 \(a_i\)。注意到图不一定连通。
首先考虑对于 \(a_i \neq a_j\) 的部分分如何解决。这种情况下,每个连通块都形成一个简简单单的环。
容易发现最优情况下,应当是先由一头起始奶牛 \(i\) 拜访 \(a_i\),然后 \(a_i\) 拜访 \(a_{a_i}\),然后 \(a_{a_i}\) 拜访 \(a_{a_{a_i}}\),以此类推。
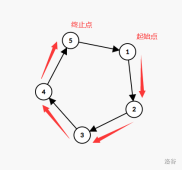
所以这种情况下,每个连通块的答案就是 \(v_i\) 的和减去这个连通块内 \(v_i\) 的最小值。
那么对于非特殊情况,我们如何解决呢?先随意画出一张可能的有向图观察一下吧。
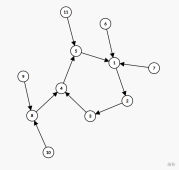
我们发现每一个连通块内有且仅有一个环,那么我们就可以把点分成两类:
- 如果这个点不在环上,我们先让它进行拜访,它一定能对答案产生贡献。(见下图)
- 如果这个点在环上,那么我们用部分分的思路推导,也一定有且仅有一个环上的点无法产生贡献。
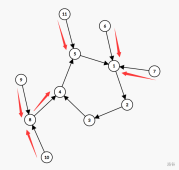
问题也就迎刃而解了。我们对于每个连通块,统计所有 \(v_i\) 的和,再减去环上的点的 \(v_i\) 的最小值,就是答案。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
int x = 0; char ch = getchar();
while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = (x<<3) + (x<<1) + ch - '0', ch = getchar();
return x;
}
const int L = 1e5 + 5;
int n, ans, minn, a[L], v[L], f[L], in[L];
vector<int> vec, son[L];
bool vis[L];
void get_point(int x) { // 获取每一个连通块中的点
vis[x] = true, vec.push_back(x);
for (int i = 0; i < son[x].size(); i++)
if (!vis[son[x][i]]) get_point(son[x][i]);
if (!vis[a[x]]) get_point(a[x]);
}
void get_circle(int x) { // dfs 找环,同时直接更新最小值
f[x]++;
if (f[x] == 2) minn = min(minn, v[x]);
if (f[a[x]] != 2) get_circle(a[x]);
}
signed main() {
n = read();
for (int i = 1; i <= n; i++)
a[i] = read(), v[i] = read(), son[a[i]].push_back(i), in[a[i]]++;
for (int i = 1; i <= n; i++) {
if (vis[i]) continue;
minn = L*L;
get_point(i);
get_circle(i);
for (int j = 0; j < vec.size(); j++)
ans += v[vec[j]];
ans -= minn;
vec.clear();
}
printf("%lld", ans);
return 0;
}
T2
题意简述
- 给定两个字符串 \(s\) 和 \(t\),仅由小写字母 'a' 到 'r' 组成。
- \(q\) 次询问,每次给出一个小写字母 'a' 到 'r' 的子集,你需要判断 \(s\) 与 \(t\) 在删去了不包含在子集内的字符后是否相等,相等输出 'Y',不相等输出 'N'。每次询问独立。
- \(\mid s \mid, \mid t \mid \leq 10^5\),\(1 \leq q \leq 10^5\)。
解题思路
首先思考暴力做法:对于每次询问,对两个字符串暴力地扫一遍,剔除不包含在自己内的字符,然后 \(O(n)\) 判断两个字符串是否相等。
时间复杂度达到了 \(O(nq)\),显然过不去。怎么办呢?
观察题面,注意到本题有一个不同寻常的限制:
仅由小写字母 'a' 到 'r' 组成。
'r' 是字母表里的第 \(18\) 个字母,而所有 'a' 到 'r' 的子集个数只有 \(2^{18} = 262144\),似乎......不是很大?
考虑使用状压 dp 预处理出答案,我们设询问子集的元素个数为 \(k\),分类如下:
- 如果 \(k = 1\),比如 'a'、'b',我们直接统计这个字符在 \(s\) 与 \(t\) 中出现的次数即可。
- 如果 \(k = 2\),比如 'ab'、'ac',我们用暴力方法判断是否相等。
- 如果 \(k \geq 3\),比如 'abc'、'defg'、'acdfh',我们发现当且仅当询问子集的所有子集的答案都是 'Y' 的时候询问子集的答案才是 'Y'。为了简化,我们只用判断询问子集的所有元素个数等于 \(k-1\) 的子集即可。
比如,对于样例中的情况,即 $s = $ "\(\texttt{aabcd}\)",$t = $ "\(\texttt{caabd}\)":
- 我们观察到两个字符串中 'a'、'b'、'c'、'd' 的数量都相同,所以:
\(dp[\)'a'\(] = dp[\)'b'\(] = dp[\)'c'\(] = dp[\)'d'\(] = true\) - 对于子集 'ab'、'ac'、'ad'、'bc'、'bd'、'cd',我们暴力判断,得出:
\(dp[\)'ab'\(] = dp[\)'ad'\(] = dp[\)'bd'\(] = dp[\)'cd'\(] = true\),\(dp[\)'ac'\(] = dp[\)'bc'\(] = true\) - 对于子集 'abc',我们发现 \(dp[\)'ab'\(] = true\),\(dp[\)'ac'\(] = dp[\)'bc'\(] = false\),不满足它所有子集答案都是 'Y',所以:
\(dp[\)'abc'\(] = false\)。 - 而对于子集 'abd',我们发现 \(dp[\)'ab'\(] = dp[\)'ad'\(] = dp[\)'bd'\(] = true\),所以 \(dp[\)'abd'\(] = true\)。
- 子集 'acd'、'bcd'、'abcd' 同理。
具体如何实现呢?我们考虑使用二进制的思想将所有 'a' 到 'r' 的子集变为一个数。比如将 'a' 转化为 \(1\)、将 'b' 转化为 \(2\)、将 'c' 转化为 \(4\)、将 'abc' 转化为 \(7\)。
同时,我们预处理出元素个数等于 \(1\) 的子集与元素个数等于 \(2\) 的子集,进行特殊处理。
代码
#include <bits/stdc++.h>
using namespace std;
inline int read() {
int x = 0; char ch = getchar();
while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = (x<<3) + (x<<1) + ch - '0', ch = getchar();
return x;
}
const int L = (2<<18);
int q, x, cnt, f1[L], f2[L], tmp1[L], tmp2[L], cnt1[20], cnt2[20];
string s, t, ask;
bool dp[L];
int main() {
cin >> s >> t;
for (int i = 0; i < s.size(); i++)
cnt1[s[i]-'a']++; // 预处理出 s 中每个字符出现的个数
for (int i = 0; i < t.size(); i++)
cnt2[t[i]-'a']++; // 预处理出 t 中每个字符出现的个数
for (int i = 0; i <= 17; i++) { // 预处理出元素个数等于 1 的子集与元素个数等于 2 的子集
f1[(1<<i)] = i+1;
for (int j = i+1; j <= 17; j++)
f1[(1<<i)+(1<<j)] = i+1, f2[(1<<i)+(1<<j)] = j+1;
}
for (int i = 1; i <= L-1; i++) {
if (f1[i] && !f2[i]) { // 元素个数等于 1 的子集
if (cnt1[f1[i]-1] == cnt2[f1[i]-1])
dp[i] = true;
else dp[i] = false;
} else if (f1[i]) { // 元素个数等于 2 的子集
if (cnt1[f1[i]-1] != cnt2[f1[i]-1] || cnt1[f2[i]-1] != cnt2[f2[i]-1])
dp[i] = false;
else {
// 暴力判断
cnt = 0;
for (int j = 0; j < s.size(); j++)
if (s[j]-'a' == f1[i]-1 || s[j]-'a' == f2[i]-1)
tmp1[++cnt] = s[j]-'a';
cnt = 0;
for (int j = 0; j < t.size(); j++)
if (t[j]-'a' == f1[i]-1 || t[j]-'a' == f2[i]-1)
tmp2[++cnt] = t[j]-'a';
dp[i] = true;
for (int j = 1; j <= cnt; j++)
if (tmp1[j] != tmp2[j])
dp[i] = false;
}
} else {
dp[i] = true, x = i;
for (int j = 17; j >= 0; j--) {
if (x < (1<<j)) continue;
x -= (1<<j);
if (!dp[i-(1<<j)]) dp[i] = false;
}
}
}
q = read();
while (q--) {
cin >> ask, x = 0;
for (int i = 0; i < ask.size(); i++)
x += (1<<(ask[i]-'a'));
if (dp[x]) printf("Y");
else printf("N");
}
return 0;
}
T3
题意简述
- 给定一个仅包含字符 'C','O' 和 'W' 的字符串 \(s\),有两种操作:
1.选择两个相邻的字符并将其删除。
2.选择一个字母,将其替换为另外两个字母的任一排列。 - \(q\) 次询问,每次询问给定 \(l, r\),问能否通过上述两种操作将 \(s\) 的子串 \([l, r]\) 变为单个字母 'C',能则输出 'Y',不能则输出 'N'。
- \(1 \leq l \leq r \leq \mid s \mid \leq 2 \cdot 10^5\), \(1 \leq q \leq 2 \cdot 10^5\)。
解题思路
比较简单的思维题。
首先思考在变化的字符串 \(s\) 中有什么是不变的。
这种题目的一个常见套路就是分析奇偶性。我们记字符 'C','O','W' 的个数为 \(c, o, w\),列出下表观察奇偶性:
我们惊奇地发现:\(c+o, o+w, w+c\) 的奇偶性自始至终都不变!
既然我们需要把字符串变成单个字符 'C',那么 \(c+o\) 就 \(w+c\) 就应该是奇数,\(o+w\) 就应该是偶数。
那么解法也呼之欲出了。我们使用前缀和维护 'c','o','w' 出现的次数,对于每一次询问,求出该子串里 \(c+o, o+w, w+c\) 的值,再判断奇偶性是否符合要求即可。
代码
#include <bits/stdc++.h>
using namespace std;
inline int read() {
int x = 0; char ch = getchar();
while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = (x<<3) + (x<<1) + ch - '0', ch = getchar();
return x;
}
const int L = 2e5 + 5;
int q, l, r, c, o, w, pre[L][3];
string s;
int main() {
cin >> s;
for (int i = 0; i < s.size(); i++) {
if (i) pre[i][0] = pre[i-1][0], pre[i][1] = pre[i-1][1], pre[i][2] = pre[i-1][2];
if (s[i] == 'C') pre[i][0]++;
else if (s[i] == 'O') pre[i][1]++;
else pre[i][2]++;
}
q = read();
while (q--) {
l = read()-1, r = read()-1;
if (l) c = pre[r][0]-pre[l-1][0], o = pre[r][1]-pre[l-1][1], w = pre[r][2]-pre[l-1][2];
else c = pre[r][0], o = pre[r][1], w = pre[r][2];
if (((c+o)&1) && ((c+w)&1) && !((o+w)&1)) printf("Y");
else printf("N");
}
return 0;
}
