L2-1 出栈序列的合法性 给定一个最大容量为 M 的堆栈,将 N 个数字按 1, 2, 3, ..., N 的顺序入栈,允许按任何顺序出栈,则哪些数字序列是不可能得到的?例如给定 M=5、N=7,则我们有可能
L2-1 出栈序列的合法性
给定一个最大容量为 M 的堆栈,将 N 个数字按 1, 2, 3, ..., N 的顺序入栈,允许按任何顺序出栈,则哪些数字序列是不可能得到的?例如给定 M=5、N=7,则我们有可能得到{ 1, 2, 3, 4, 5, 6, 7 },但不可能得到{ 3, 2, 1, 7, 5, 6, 4 }。
输入格式:
输入第一行给出 3 个不超过 1000 的正整数:M(堆栈最大容量)、N(入栈元素个数)、K(待检查的出栈序列个数)。最后 K 行,每行给出 N 个数字的出栈序列。所有同行数字以空格间隔。
输出格式:
对每一行出栈序列,如果其的确是有可能得到的合法序列,就在一行中输出YES,否则输出NO。
输入样例:
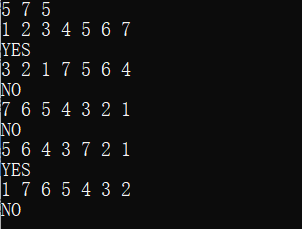
5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2
输出样例:
YES
NO
NO
YES
NO
这道题我们的思路是先用一个队列把输入的数存进去,然后再把1到n的数存到栈里,如果存入栈中的数与队列的第一个数相等,就pop()。
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
int main()
{
int m,n,k;
cin>>m>>n>>k;
for(int i=0;i<k;++i)
{
stack<int> s;//在第一个for循环里面定义栈和队列,省的自己清空
queue<int> q;
for(int j=0;j<n;j++)//把输入的数存到队列里
{
int a;
cin>>a;
q.push(a);
}
int num=1;
while(s.size()<m&&!q.empty())//防止超出栈的容量,保证q非空
{
s.push(num);
num++;
while(!s.empty()&&!q.empty()&&s.top()==q.front())//有相等就取出
{
s.pop();
q.pop();
}
if(num==n+1) break;//栈满之后就跳出
}
if(num==n+1&&q.size()==0&&s.size()==0) cout<<"YES"<<endl;//跳出后,栈和队列中的元素都pop完了,说明该序列可以实现
else cout<<"NO"<<endl;
}
return 0;
}