C++设计模式 - 解析器模式（Interpreter）

领域规则模式

• 在特定领域中,某些变化虽然频繁,但可以抽象为某种规则。这时候,结合特定领域,将问题抽象为语法规则,从而给出在该领域下的一般性解决方案。

典型模式

• Interpreter

Interpreter 动机( Motivation )

• 在软件构建过程中,如果某一特定领域的问题比较复杂 ,类似的结构不断重复出现,如果使用普通的编程方式来实现将面临非常频繁的变化。
• 在这种情况下,将特定领域的问题表达为某种语法规则下的句子，然后构建一个解释器来解释这样的句子,从而达到解决问题的目的。

模式定义

给定一个语言,定义它的文法的一种表示，并定义一种解释器，这个解释器使用该表示来解释语言中的句子。

结构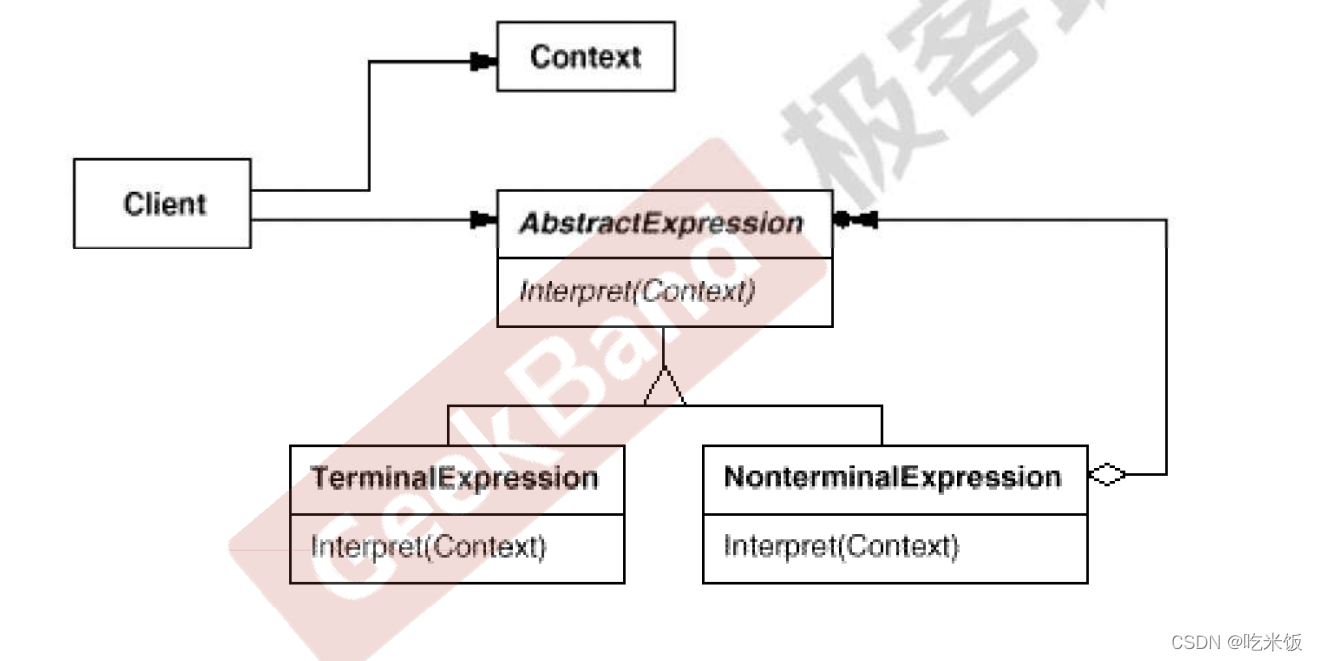

要点总结

• Interpreter模式的应用场合是Interpreter模式应用中的难点,只_有满足“业务规则频繁变化,且类似的结构不断重复出现，并且容易抽象为语法规则的问题”才适合使用Interpreter模式。
• 使用Interpreter模式来表示文法规则,从而可以使用面向对象技巧来方便地"扩展”文法。
• Interpreter模式比较适合简单的文法表示,对于复杂的文法表示，Interperter模式会产生比较大的类层次结构, 需要求助于语法分析生成器这样的标准工具。

cpp

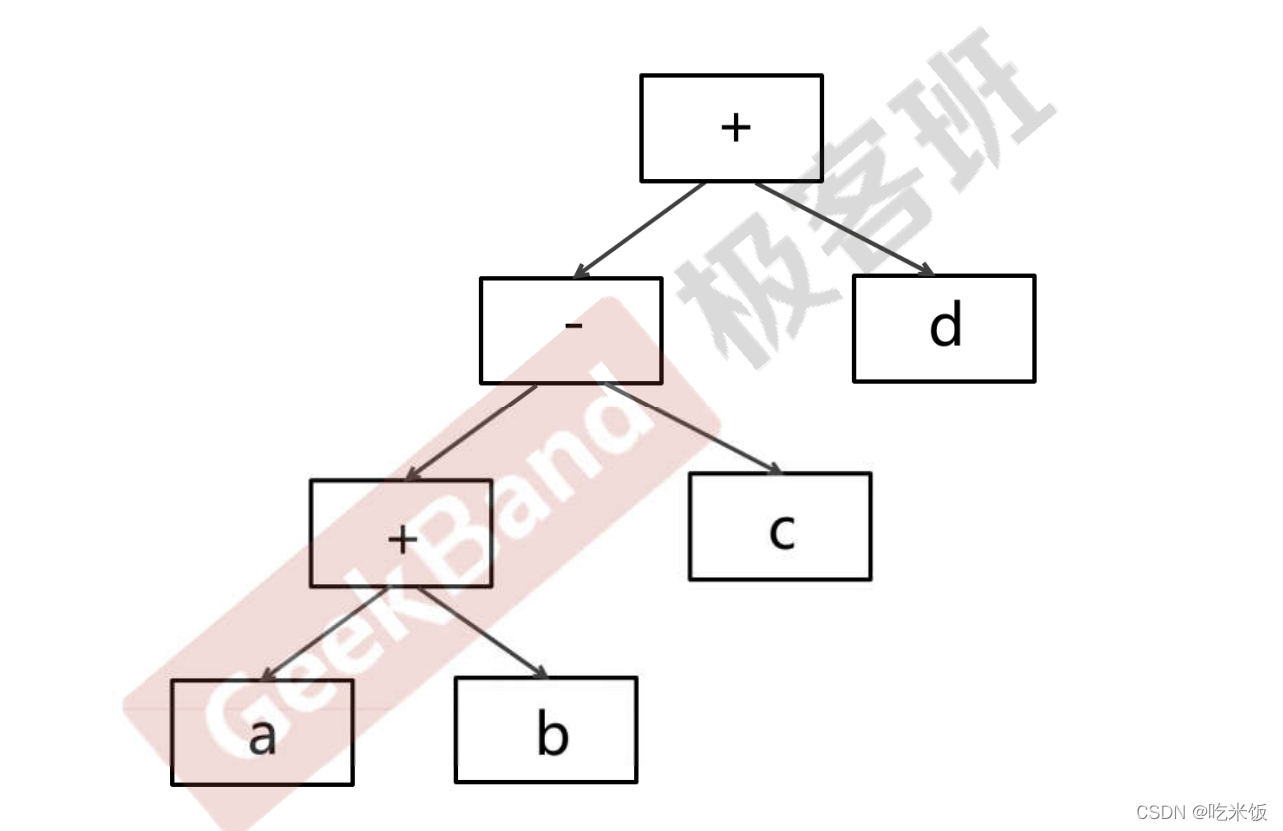
#include<iostream>
#include<map>
#include<string>
#include<stack>

class Expression
{
public:
	virtual int interpreter(std::map<char, int>) = 0;
	virtual ~Expression() {}
};

class VarExpression :public Expression
{
public:
	VarExpression(const char& k) :key(k) {}
	int interpreter(std::map<char, int>var) override
	{
		return var[key];
	}

private:
	char key;
};

class SymbolExpression :public Expression
{
public:
	SymbolExpression(Expression* l, Expression* r) :left(l), right(r) {}
protected:
	Expression* left;
	Expression* right;
};

class AddExpression : public SymbolExpression
{
public:
	AddExpression(Expression* left, Expression* right) :SymbolExpression(left, right) {}
	int interpreter(std::map<char, int> var) override
	{
		return left->interpreter(var) + right->interpreter(var);
	}
};

class SubExpression :public SymbolExpression
{
public:
	SubExpression(Expression* left, Expression* right) :SymbolExpression(left, right) {}
	int interpreter(std::map<char, int> var) override
	{
		return left->interpreter(var) - right->interpreter(var);
	}
};
class MulExpression :public SymbolExpression
{
public:
	MulExpression(Expression* left, Expression* right) :SymbolExpression(left, right) {}
	int interpreter(std::map<char, int> var) override
	{
		return left->interpreter(var) * right->interpreter(var);
	}
};

class DivExpression :public SymbolExpression
{
public:
	DivExpression(Expression* left, Expression* right) :SymbolExpression(left, right) {}
	int interpreter(std::map<char, int> var) override
	{
		return left->interpreter(var) / right->interpreter(var);
	}
};

Expression* analyse(std::string expStr)
{
	std::stack<Expression*> expStack;
	Expression* left = nullptr;
	Expression* right = nullptr;
	for (int i = 0; i < expStr.size(); ++i)
	{
		switch (expStr[i])
		{
		case '+':
			// 加法运算
			left = expStack.top();
			right = new VarExpression(expStr[++i]);
			expStack.push(new AddExpression(left, right));
			break;
		case '-':
			// 减法运算
			left = expStack.top();
			right = new VarExpression(expStr[++i]);
			expStack.push(new SubExpression(left, right));
			break;
		case '*':
			// 乘法运算
			left = expStack.top();
			right = new VarExpression(expStr[++i]);
			expStack.push(new MulExpression(left, right));
			break;
		case '/':
			// 除法运算
			left = expStack.top();
			right = new VarExpression(expStr[++i]);
			expStack.push(new DivExpression(left, right));
			break;
		default:
			// 变量表达式
			expStack.push(new VarExpression(expStr[i]));
		}
	}
	Expression* expression = expStack.top();
	return expression;
}

void release(Expression* expression) {

	//释放表达式树的节点内存...
}

int main()
{
	std::string expStr = "a+b-c+d-e*f/g";
	std::map<char, int> var;
	var.insert(std::make_pair('a', 5));
	var.insert(std::make_pair('b', 2));
	var.insert(std::make_pair('c', 1));
	var.insert(std::make_pair('d', 6));
	var.insert(std::make_pair('e', 10));
	var.insert(std::make_pair('f', 8));
	var.insert(std::make_pair('g', 4));

	Expression* expression = analyse(expStr);
	int result = expression->interpreter(var);
	std::cout << result << std::endl;

	release(expression);

	return 0;
}