树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根在上,而叶在下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点。除根节点外,其余结点被分成m(m > 0)个互不相交的集合T1、T2、…… 、Tm,其中每一个集合Ti(1 <= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,但可以有0个或多个后继。
由此可知,树是递归定义的。
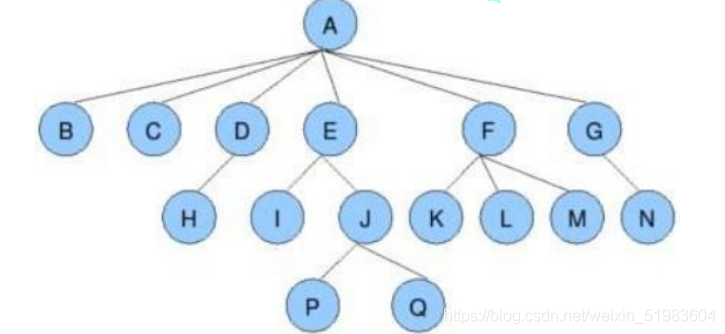
下面是一个简单的树。
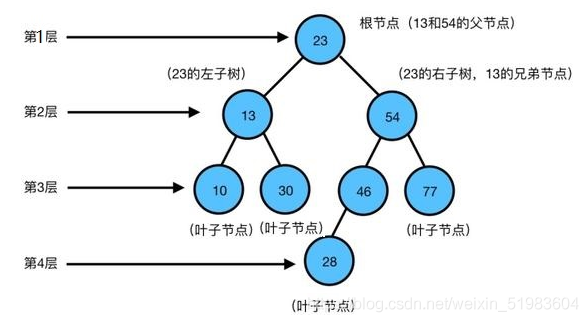
图中根节点就是没有父结点的结点,叶子结点就是没有子节点的结点。
还要注意:树的子树是不相交的;除了根节点外,每个结点有且仅有一个父结点。
二叉树 二叉树的概念及结构 概念
下面介绍一些与树相关的概念(以上面的树为例):
(1)结点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的为6,即B、C、D、E、F、G。
(2)叶结点:度为0的节点称为叶结点;如上图:B、C、H、I…等为叶结点。
(3)双亲结点或父结点:若一个节点含有子结点,则这个结点称为其子结点的父结点;如上图:A是B的父结点。
(4)孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点;如上图:B是A的孩子节点。
(5)兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点。
(6)树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6。
(7)结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推。
(8)树的高度或深度:树中结点的最大层次; 如上图:树的高度为4。
(9)节点的祖先:从根到某一结点所经分支上的所有结点;如上图:D、A是H的祖先;A是所有结点的公共祖先。
(10)子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙。
(11)森林:多棵互不相交的树的集合称为森林。
结构一棵二叉树是结点的一个有限集合,该集合为空,或者是由一个根节点加上两棵称为左子树和右子树的二叉树组成。
二叉树的特点:
(1)每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
(2)二叉树的子树有左右之分,其子树的次序不能颠倒。
特殊的二叉树
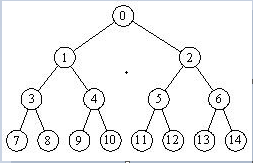
(1)满二叉树
每一层的结点数都达到最大值,则这个二叉树就是满二叉树。
也就是说,如果一个二叉树的层数为K(根节点是第1层),且结点总数是(2^k) -1 ,则它就是满二叉树。
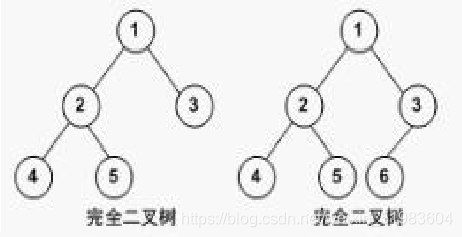
(2)完全二叉树
完全二叉树是由满二叉树而引出来的。对于深度为K的、有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 满二叉树是一种特殊的完全二叉树。
也就是说:完全二叉树的叶子结点只能出现在最下层和次下层,且最下层的叶子结点从左到右连续;前K-1层是满的二叉树。
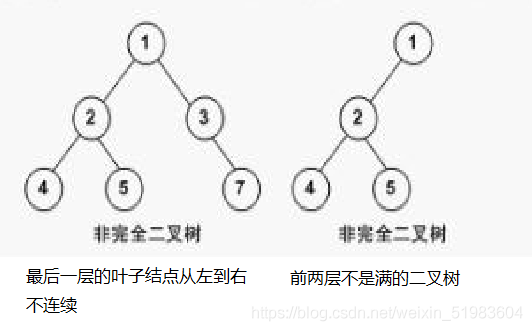
非完全二叉树
Java实现二叉树以及遍历代码
1 package com.mm.BinaryTree; 2 3 public class BinaryTree { 4 Node root; // 首先定义一个根节点 5 // 定义一个往二叉树添加节点的方法 6 // 利用递归实现 7 public Node addNode(Node temp,int value){ 8 Node newNode = new Node(value); 9 if(temp == null){ // 如果二叉树是空的 就将传进来的参数作为根节点创建一个根节点 10 temp = newNode; 11 return temp; 12 } 13 else if (value < temp.data){ // 如果传进来的参数小于根节点的值 就用这个值去和左子节点去比较 添加到左子节点 14 temp.left = addNode(temp.left,value); 15 } 16 else { 17 temp.right = addNode(temp.right,value); // 如果传进来的参数大于根节点的值,就用这个值去和右子节点去比较,添加到右子节点 18 } // 递归调用添加方法 直到子节点的值为空把数添加进去位置 19 return temp; 20 } 21 22 // 定义前序遍历的方法 先根再左再右 23 public void qianXuPrint(Node root){ 24 // 依然使用递归实现 25 if(root != null){ 26 System.out.print(root.data+" "); // 先把根节点打印出来 27 qianXuPrint(root.left); // 遍历左子节点 打印最左子节点的值然后逐层上移打印左子节点 也就是最左子节点的二叉树的根 28 qianXuPrint(root.right); // 遍历右子节点 29 } 30 } 31 32 // 定义中序遍历的方法 先左再根再右 33 public void zhongXuPrint(Node root){ 34 if(root != null){ 35 zhongXuPrint(root.left); // 遍历左子节点 打印最左子节点的值然后逐层上移打印左子节点 也就是最左子节点的二叉树的根 36 System.out.print(root.data+" "); // 打印最左子节点 37 zhongXuPrint(root.right); // 遍历右子节点 38 } 39 } 40 41 // 定义后序遍历的方法 先左再右再根 42 public void houXuPrint(Node root){ 43 if(root != null){ 44 houXuPrint(root.left); // 遍历左子节点 打印最左子节点的值然后逐层上移打印左子节点 也就是最左子节点的二叉树的根 45 houXuPrint(root.right); // 遍历右子节点 打印最右子节点的值然后逐层上移打印右子节点 也就是最右子节点的二叉树的根 46 System.out.print(root.data+" "); // 打印根节点 47 } 48 } 49 } 50 51 class Node{ 52 // 定义一个节点类 53 int data; // 根节点 54 Node left; // 定义左节点 55 Node right; // 定义右节点 56 57 public Node(int data) { 58 this.data = data; 59 this.left = null; 60 this.right = null; 61 } 62 63 public int getData() { 64 return data; 65 } 66 67 public void setData(int data) { 68 this.data = data; 69 } 70 71 public Node getLeft() { 72 return left; 73 } 74 75 public void setLeft(Node left) { 76 this.left = left; 77 } 78 79 public Node getRight() { 80 return right; 81 } 82 83 public void setRight(Node right) { 84 this.right = right; 85 } 86 87 @Override 88 public String toString() { 89 return "Node{" + 90 "data=" + data + 91 ", left=" + left + 92 ", right=" + right + 93 '}'; 94 } 95 } 96 // 测试用例 97 package com.mm.BinaryTree; 98 99 public class BinaryTreeTest { 100 public static void main(String[] args) { 101 // 将一个数组中的数构成一个二叉树 102 int [] arr = {5,8,2,3,1}; 103 BinaryTree bt = new BinaryTree(); 104 Node root = null; // 定义一个根节点 105 106 for(int i=0;i<arr.length;i++){ 107 root = bt.addNode(root,arr[i]); 108 } 109 110 // 调用前序遍历 111 System.out.print("前序遍历: "); 112 bt.qianXuPrint(root); 113 System.out.println(); 114 System.out.print("中序遍历: "); 115 bt.zhongXuPrint(root); 116 System.out.println(); 117 System.out.print("后序遍历: "); 118 bt.houXuPrint(root); 119 120 } 121 }
本文部分概念内容参考自:https://blog.csdn.net/weixin_51983604/article/details/116451530