O. Marfoq, G. Neglia, L. Kameni, and R. Vidal, “Personalized Federated Learning through Local Memorization,” arXiv:2111.09360 [cs, stat], Mar. 2022, Accessed: Mar. 19, 2022. [Online]. Available: http://arxiv.org/abs/2111.09360
这篇蔚蓝海岸大学埃森哲技术研究院的文章同样在研究PFL,而且大有顶会论文的趋势。该团队对于PFL的理解为在对每个用户训练得到单独模型的同时,还要利用其他用户的知识。因此,这篇文章的思路依然是对相似用户进行聚类。那么聚类标准是什么呢?每个用户对输入的表示(embedding)。之前我一直觉得embedding的训练比较难,其实就是每个用户分类层的前一层的输出。比如CNN的最优一个卷积层,RNN的最后一个隐藏状态。这样聚类没有触及到最优的分类,因此避免了隐私的泄露,但是又利用了用户对数据进行表征的网络,还是比较巧妙。
然后根据聚类结果对他们的网络进行融合,在两个用户聚类的时候,依然是典型的需要调参的融合方式
\[h_{m, \lambda_{m}}(\mathbf{x}) \triangleq \lambda_{m} \cdot h_{\mathcal{S}_{m}}^{(k)}(\mathbf{x})+\left(1-\lambda_{m}\right) \cdot h_{\mathcal{S}}(\mathbf{x}) \]这也是体现了标题local memorization的作用,就是利用了邻居的记忆。今天谷歌有一篇文章,也是将多个微调的模型直接进行聚合,在ImageNet1K上取得了90%的准确率,可谓是异曲同工。同时这篇文章也分析了generalization bound。最终的实验结果看起来也不错
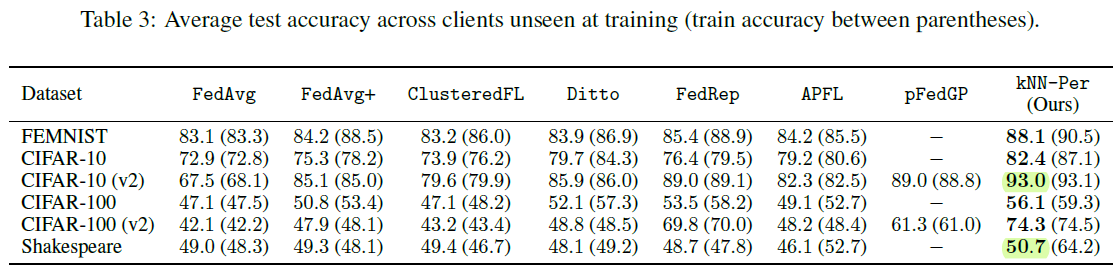
可以看到,对于每个用户两个class的CIFAR10而言,准确率已经达到了93,更不要说MNIST了。不过Shakespeare数据集的提升还是并不明显,可能这种PFL的思路还是对对象识别更加有效。
C. Hou, K. K. Thekumparampil, G. Fanti, and S. Oh, “FedChain: Chained Algorithms for Near-Optimal Communication Cost in Federated Learning,” arXiv:2108.06869 [cs, math], Mar. 2022, Accessed: Mar. 19, 2022. [Online]. Available: http://arxiv.org/abs/2108.06869
这是CMU发表在ICLR 2022上的文章,以收敛性分析为主。对于FedAvg遭遇的异构数据瓶颈,这篇文章没有迎难而上研究PFL,而是选择直接逃避。既然FL对iid的数据效果好,那就只对iid做就好了呀,对于non iid的数据,直接回到原来的SGD,不就等效于全局的训练,那异构数据的问题也就迎刃而解了。
当然作者不会直接这么说,故事还是要好好讲的。作者的意思是FedAvg算法的本地训练阶段能够利用用户数据的相似性加速训练,而SGD算法能够在异构数据下得到更低错误概率。文章中的图比较形象,确实是离最优点远的时候,虽然梯度有差别但是方向基本一致,到训练后期才体现出每个client的差别,从而需要频繁使用global training
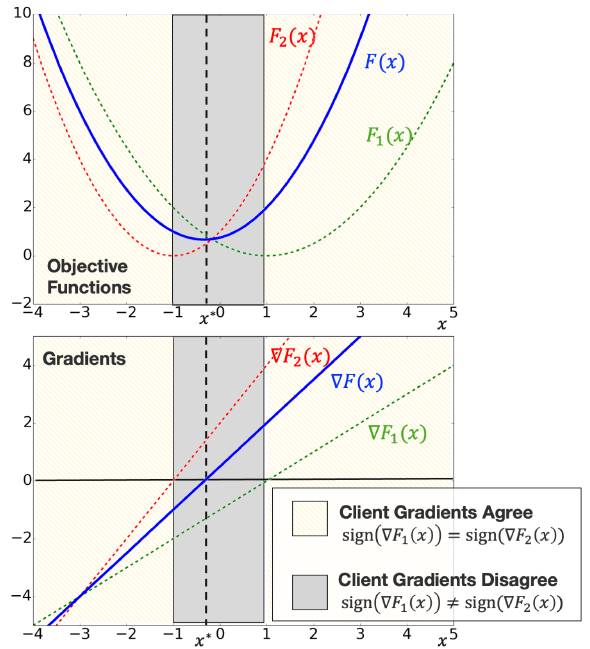
对于用户异构性而言,为了理论分析方便的定义被说成了standard measure,其实不太客观
\[\zeta^{2}:=\max _{i \in[N]} \sup _{x}\left\|\nabla F(x)-\nabla F_{i}(x)\right\|^{2} \]按照这个思路,文章提出的FedChain就是先进行若干轮FedAvg算法,然后进行SGD算法,

这篇文章在理论分析方面做了很多工作(堆料)。在仿真方面,实验表示仅仅训练一轮FedAvg都能有明显的提高,表明确实是有效果的
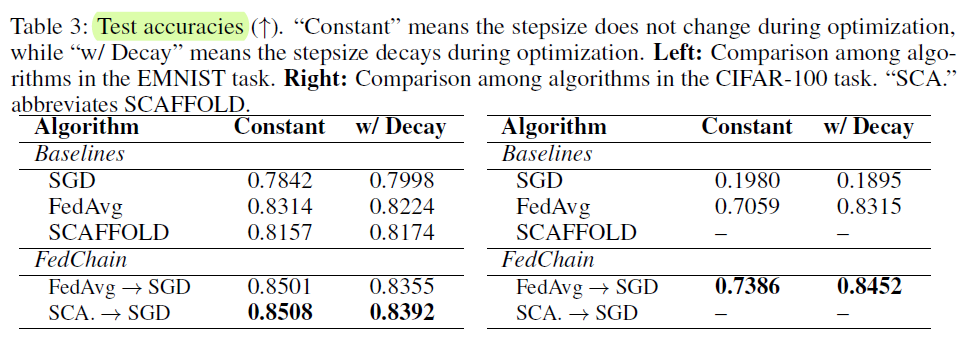 量化
量化
C. Tang et al., “Mixed-Precision Neural Network Quantization via Learned Layer-wise Importance,” arXiv:2203.08368 [cs], Mar. 2022, Accessed: Mar. 19, 2022. [Online]. Available: http://arxiv.org/abs/2203.08368
这篇来自于清华大学的神经网络混合精度量化的文章,初看让人眼前一亮,细看还是故事讲得比做的好。文章首先讲明了混合精度量化的重要性,现有算法的难点,他们观察到一个可训练的变量能够表征每一层对于量化的敏感程度或者说重要性,然后由此得到一个整数规划来分配每一层的量化比特数量。
这个量化的思路有点霍夫曼编码在神经网络中的应用。霍夫曼编码根据码字出现的概率来分配码长,这篇文章则根据每一层的重要性来选择码长。那么文章的核心当然就是如何衡量重要性了。经济学中常用的shapley value大家也早就想过了,但这个毕竟是个组合问题,搜索空间大耗时长,就算用DRL也不好搞。那能不能用一次端到端的学习,学到一些参数,刚好就和重要性对应上,相当于找一个shapley value的平替呢?之前大家也不是没想过,BN层的scale factor就可以反映数据输入的聚集程度,大家也这么做了。但是BN层的映射变换是在前一层量化操作后,也就是说不能直观反映量化带来的的变化。所以这篇文章提出用每一层的scaling factor来表征重要性,也就是下面的\(s\)
\[v^{q}=Q_{b}(v ; s)=\operatorname{round}\left(\operatorname{clip}\left(\frac{v}{s}, \min _{b}, \max _{b}\right)\right) \times s \]具体的好处直接放原文,总之\(s\)在quantization-aware training中就能得到优化,能够有效反映quantization的性质。
As shown in Equation 1, during QAT, the scale factor of the quantizer in each layer is trained to adjust the corresponding quantization mapping properly at a specific bit-width. This means that it can naturally capture certain quantization characteristics to describe the layers due to its controlled quantization mapping being optimized directly by the task loss. Therefore, there should be numerically significant difference in the scale factors for heterogeneous layers in a network.
Moreover, the operation involved in the scale factor takes place in the quantizer, which allows it to be directly aware of quantization.
Last but not least, there are two quantizers for activations and weights for a layer, respectively, which means that we can obtain the importance of weights and activations separately. In contrast, we cannot get the importance of weights through the BN layer since it only acts on activations.
之后作者实验验证了这个想法。(这里没看懂是大的scale factor需要更多位数还是小的需要更多位数,从下面的优化问题来看是小的factor需要更多位数,也就是基本不缩放的重要性高,所以分配更多位数,和图里的又对不上)
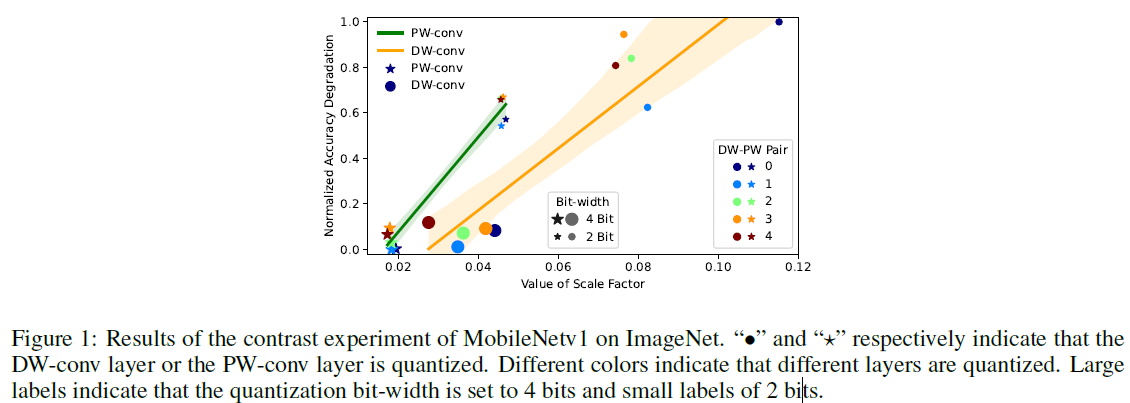
最终得到了整数规划,用来求解每层需要分配的量化数量。

