450. 删除二叉搜索树中的节点 思路: 情况一 A 恰好是末端节点,两个子节点都为空,那么它可以当场去世了: 情况二 A 只有一个非空子节点,那么它要让这个孩子接替自己的位置: 情
思路:
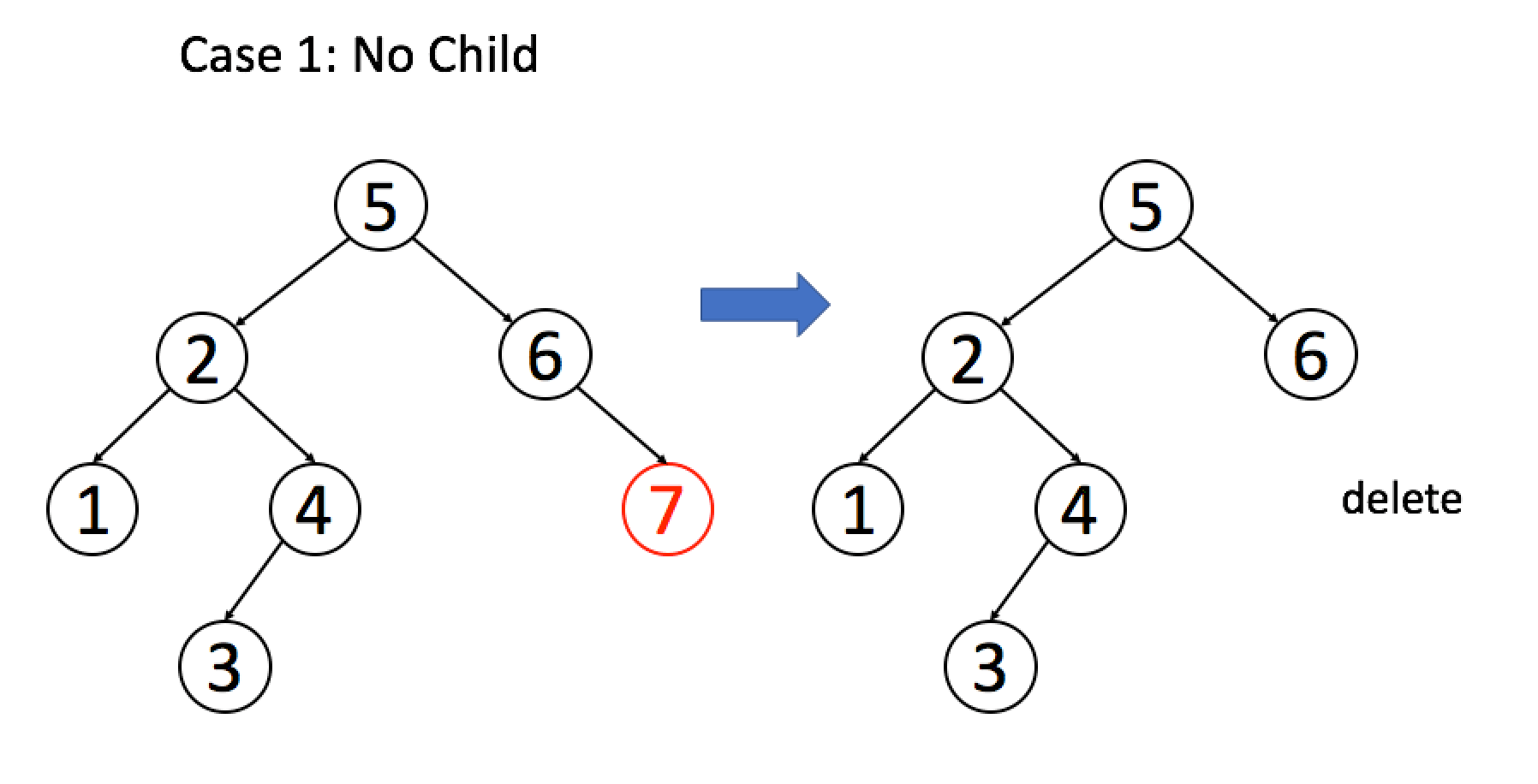
情况一
A 恰好是末端节点,两个子节点都为空,那么它可以当场去世了:
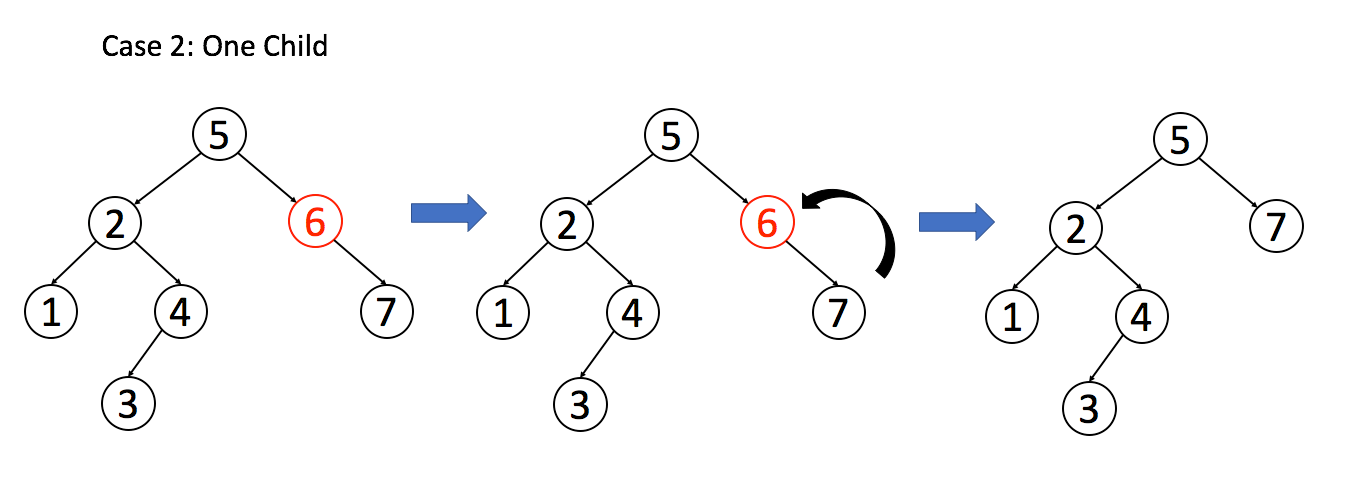
情况二
A 只有一个非空子节点,那么它要让这个孩子接替自己的位置:
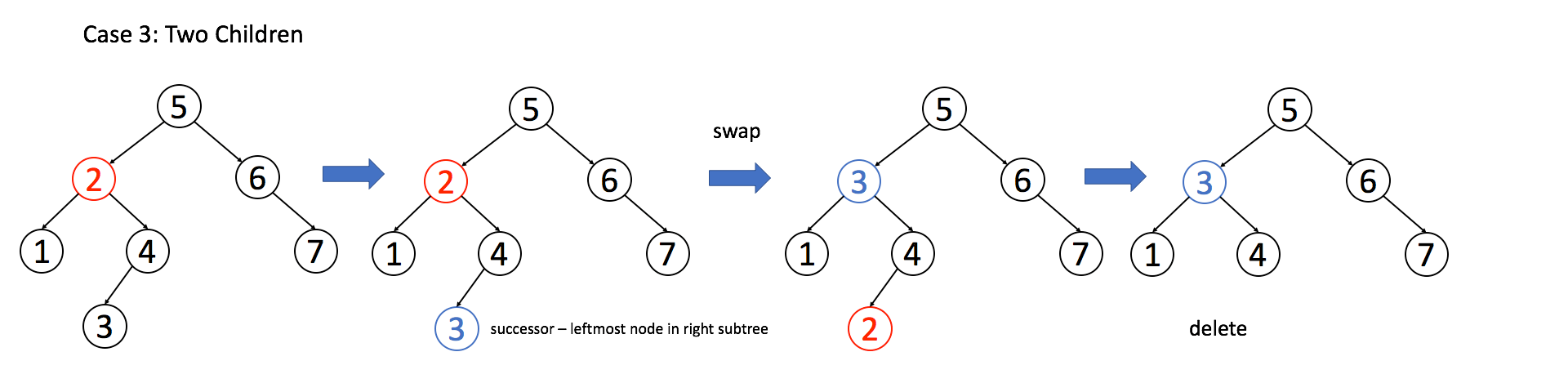
情况三
A 有两个子节点,麻烦了,为了不破坏 BST 的性质,A 必须找到左子树中最大的那个节点或者右子树中最小的那个节点来接替自己,我的解法是用右子树中最小节点来替换:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null) return null;
if(root.val == key){
//两种判断解决了两种情况
if(root.left == null ) return root.right;
if(root.right == null ) return root.left;
//处理root结点有两个子节点的情况
//取得右子树最小值
TreeNode minNode = getMin(root.right);
//删除右子树中的最小的节点
//先将问题全部描述展开,再由尽头“返回”依次解决每步中剩余部分的问题
root.right = deleteNode(root.right, minNode.val); ()
//使用右子树最小的节点进行替换root
minNode.left = root.left;
minNode.right = root.right;
root = minNode;
}
else if(root.val > key){
//在将问题转换为子问题描述的每一步,都解决该步中剩余部分的问题。
root.left = deleteNode(root.left ,key);
} else if(root.val < key){
root.right = deleteNode(root.right ,key);
}
return root;
}
TreeNode getMin(TreeNode node){
//BST最左边的就是最小的
while(node.left != null ) node = node.left;
return node;
}
}
反思:
递归算法一碰到就理解不了,头大。参考下面文章和自己的理解后,得出和文章相同的结论。
怎么更好地终极理解递归算法
递归代码中共有四个if判断,分别对应着
- 根节点为空,返回null
- 根节点就是要删除的节点
- 要删除的节点在当前节点的左子树中(root.val > key)
- 要删除的节点在当前节点的右子树中(root.val < key)
遇到3,4情况就需要递归(递归剩下的部分,一层一层的递归),直到遇到1,2这种情况,返回确切的值。
因为是基于BFS的特殊性质(左节点< 根节点 < 右节点),在寻找右子树的最小节点时,可以通过一直遍历左节点来获得当前树结构的最小值。
