对载荷谱进行雨流计数的几个主要步骤（以四点雨流计数为例）

对载荷谱进行雨流计数的几个主要步骤（以四点雨流计数为例）

1. 滤除小幅值(Hysteresis Filtering)
2. 峰谷滤波(Peak-Valley Filtering)
3. 离散化(Discretization)
4. 四点法雨流计数(Four Point Counting Method)

• 滤除小幅值

第一步滤除时域数据中不造成损伤的小幅值。小幅值滤波的实现是通过定义一个门槛值，小于门槛值的小幅值载荷将会被去除，在原始谱中包含有大量的小载荷，删除掉这些小载荷可以节省很多的实验时间。关于低载删除目前还没有公认的标准，在一些文献和实践中倒是提出了几种准则可以参考：1、最大幅值载荷的10%~14%；2、疲劳极限的70%；3、疲劳极限的50%。

需要注意的是所有的这些参考都是基于一个原则：我们一方面要在低载删除时应尽可能的小以保证试验谱的真实性，另一方面删除的低载值也要尽可能的大以此来降低我们的试验时间和试验费用，所以需要折中考虑。

滤除小幅值前后数据对比如图：

• 峰谷滤波（只保留峰谷点的载荷值）

第二步是将滤除小幅值的数据进行峰谷滤波。如图所示仅保留峰谷值，中间过渡点全部去除。

• 离散化（将间隔的时间重新排列）

第三步是将峰谷滤波后数据进行离散化。如图所示的例子中按照峰峰值把数据划分为区间相等的六个区域，并且把第二步保留的峰谷值修正为每个对应小区间(Bin)的中间值。

• 四点雨流计数

  四点雨流计数法，依据时间序列读入时域数据的四个数据点，如果中间两个数据点构成的幅值被第一个和第四个点构成的幅值包含，则将中间这两个点构成的相对较小的载荷循环记作一次计数，并从原时域数据中删除中间这两个点，然后如法炮制的对剩余的数据点构成的新的载荷序列进行四点法雨流计数。如果中间两个点构成的幅值没有被第一和第四个点构成的幅值包含，则什么都不做，对下一个“四点”如法炮制的进行处理。当这套流程进行到最后的时候，会留下一个大的载荷循环“骨架”。按照“四点法计数”规则，在不做任何处理的情况下这个“骨架”无法再计数出任何新的结果。这个“骨架”我们习惯上称之为Residue。接着再将好多段Residue“首尾相接”进行雨流计数。这个时候，按照四点法雨流计数法则，本来数不出什么结果的，但拼接后的Residue又能贡献出新的载荷循环。而且，这些载荷循环都是幅值非常大的载荷循环，循环周次不多，但是实际形成的伪损伤数值可是不小的，因此不仅不能忽略，而且是要小心谨慎。对residue的循环计数处理，采用拼接的方法得到载荷谱，再继续雨流计数。最后对于无法再计完整循环的峰谷点，把相邻的两个数值记为半个循环。 参考文章【载荷数据处理-幅值域分析方法】雨流计数_操作稳定性测试__汽车测试网 (auto-testing.net)
  
  

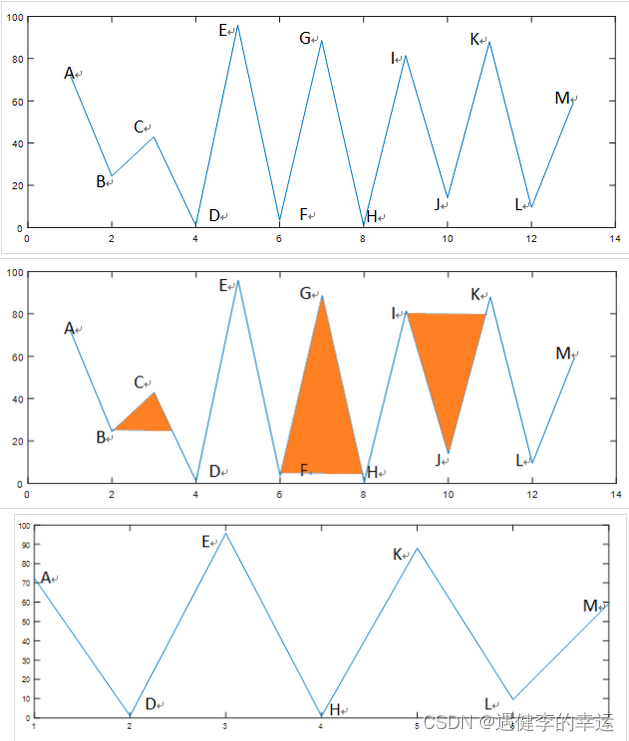
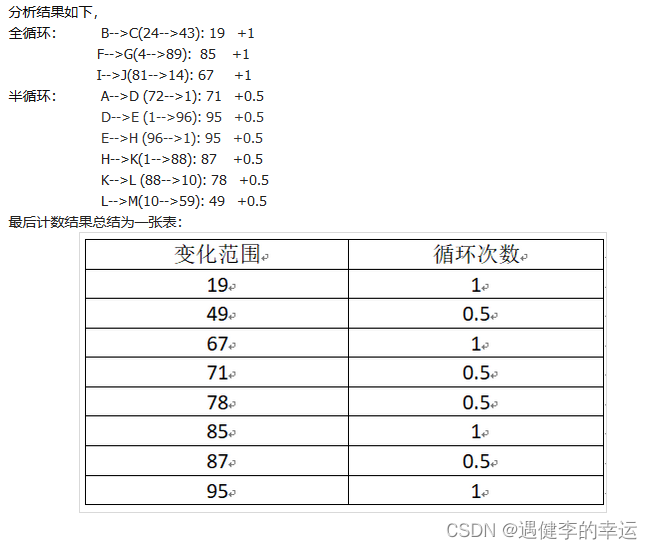
  • 残差的另一种处理方法--------将无法再分解的残差进行复制重组新的时间载荷序列，然后再雨流计数

  处理过程为
  

  处理方法为，将剩余残差序列，进行复制一份，将两份相同的残差序列的一头一尾进行连接从而形成新的载荷谱进行雨流计数分析（前后方法必须相同），接头处无法对接时，则加一时间点进行连接.
  

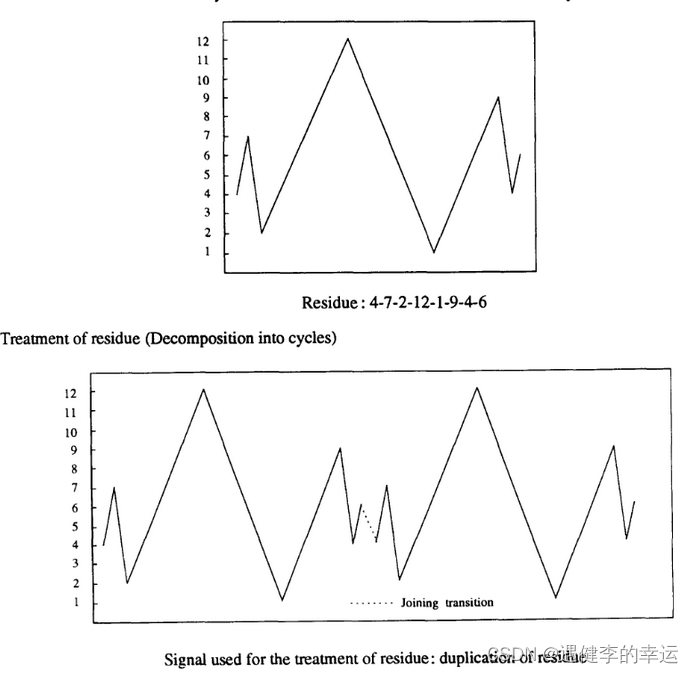
  以提取的循环 +残基的形式表达每个序列最终的雨流计数结果。该技巧可以很大程度上减少半循环的存在，从而减少寿命预测的计算

  参考文章： 试验那点事之六二：雨流计数 (qq.com)

  低载删除参考文献：[1] HEULER P, SEEGER T. A criterion for omission of variable amplitude loading histories[J]. International Journal of Fatigue, 1986, 8(4): 225–230. DOI:10.1016/0142-1123(86)90025-3.

  附录 参考CSDN博主「TANG 杰出的杰出」博文的代码：

  原文链接：https://blog.csdn.net/u011391128/article/details/79551601

  MATLAB实现代码如下:

  %% 四点雨流计数法 %%
  clear
  clc
  C=xlsread('load_F1');%%%%%%%%%在此修改加载的文件名，数据格式一致才可正确运算%%% %%也可以自己生成一个随机列向量C=randi([-100,100],1000,1)作为载荷谱输入%%
  B=C;A=C;
  q=length(A);
  %四点循环计数法
  %% 步骤一 %%
  %对载荷时间历程进行处理使它只包含峰谷峰谷交替出现
  m=q;
  for i=2:1:m-1
      if A(i-1)<a(i)&&a(i)<a(i+1)< span=""></a(i)&&a(i)<a(i+1)<>
          B(i)=NaN;
      elseif A(i-1)>A(i)&&A(i)>A(i+1)
          B(i)=NaN;
      end
  end
  B(isnan(B))=[];n=length(B);
  %% 步骤二 %%
  F=[];J=[];D=B;
  while fun(B)==1||fun(B)==0
   if fun(B)==1
      for j=1:n-4
      s1=abs(B(j+1)-B(j+2));
      s0=abs(B(j+3)-B(j));
      e3=(B(j+2)+B(j+1))/2;
          if s1<=s0< span="">
              F=[F;s1];
              J=[J;e3];
              B(j+1)=[];
              B(j+1)=[];
              n=length(B);
              break
          else
              continue
          end
      end
   elseif fun(B)==0
       break
   end
   continue
  end
  %% 步骤三 %%
  %画图像 三维hist三维图像
  X=[J,F];
  figure;hist3(X,[30 30]);
  xlabel('均值');
  title('雨流计数法-四点循环计数运算逻辑');
  ylabel('幅值');
  zlabel('循环次数');