最长有效括号的问题

作者: Grey

原文地址：最长有效括号的问题

题目链接

LeetCode 32. 最长有效括号

主要思路

设置dp数组，长度和原始字符串的长度一样，

dp[i]表示：必须以i位置字符结尾的字符串的最长有效括号子串的长度是多少。

显然有：

dp[0] = 0; // 必须以0位置的字符结尾的最长有效括号子串是0
dp[1] = (str[1] == ')' && str[0] == '('?2:0); // 必须以1位置的字符结尾的最长有效括号子串，如果满足`()`则为2，否则都是无效子串，返回0

然后看任意一个普遍位置i

如果i位置的字符是(，则

dp[i] = 0

因为一个有效的括号子串的结尾不可能是(

如果i位置的字符是)，则要分以下几种情况，假设我们以i=6为例，如下示例图

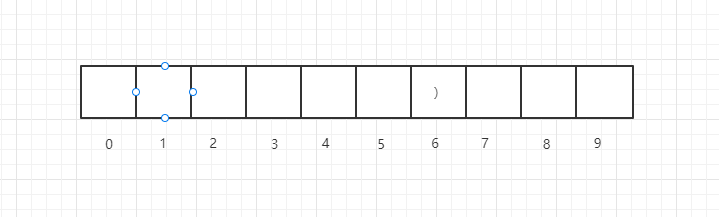
此时，如果i-1即5位置是(，如下示例

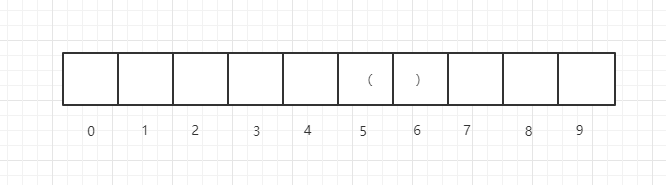
那么i位置的一种决策是：i位置和i-1先组成一个有效括号子串，长度是2，然后加上dp[i-2]的值，即：

dp[i] = dp[i-2] + 2

如果i-1位置，即5位置是)，如下示例：

假设dp[i-1]即：dp[5] = 4，即str[2]位置一定是(，如下图

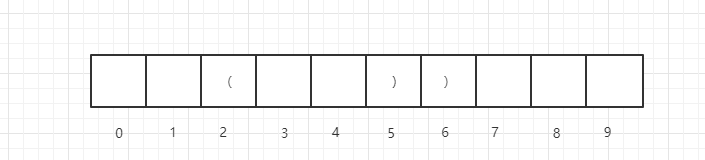
此时，分两种情况，如果str[1]位置上是(,即：

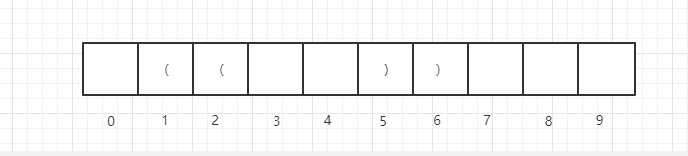
那么此时：

dp[6] = dp[5] + 6位置上的一个右括号+1位置上的一个左括号 + dp[0]，即：dp[i] = dp[i-1] + 2 + dp[(i-1) - dp[i-1] - 1]

如果str[1]位置上是)，即：

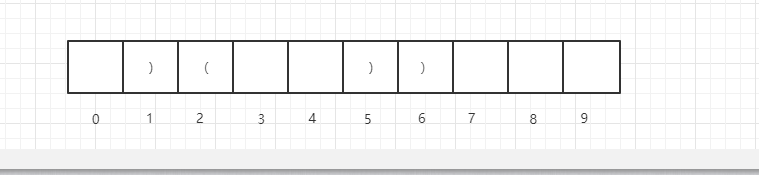
那么此时，dp[1]一定等于0，因为如果dp[1]不等于0，那么就意味着以1结尾的最长有效括号子串大于0，那么dp[5]就不止可以扩到2位置了，与我们假设的条件矛盾，所以，当dp[6]为)，且dp[1]为)的时候，dp[6]一定等于0。

自此，所有可能性分析完毕。完整代码如下：

    public static int longestValidParentheses(String s) {
        if (s == null || s.length() <= 1) {
            return 0;
        }
        char[] str = s.toCharArray();
        // dp[i]：必须以i位置符号结尾的字符串，最长有效括号串长度是多少
        int[] dp = new int[str.length];
        // dp[0] = 0, dp[1] = 0
        dp[1] = str[0] == '(' && str[1] == ')' ? 2 : 0;
        int ans = dp[1];
        for (int i = 2; i < str.length; i++) {
            if (str[i] == ')') {
                // 这才是有效情况
                if (str[i - 1] == '(') {
                    dp[i] = dp[i - 2] + 2;
                } else {
                    if ((i - 1) - dp[i - 1] >= 0 && str[(i - 1) - dp[i - 1]] == '(') {
                        dp[i] = dp[i - 1] + 2 + ((i - 1) - dp[i - 1] > 0 ? dp[(i - 1) - dp[i - 1] - 1] : 0);
                    }
                }
            }
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }

算法和数据结构笔记