作为一款教学用具,几何画板可以用于函数和几何的画图,让学生理解起来更加直观,今天小编就来介绍一下使用椭圆第二定义来得到目标图形的方法吧,增加大家对抽象概念的理解。
作为一款教学用具,几何画板可以用于函数和几何的画图,让学生理解起来更加直观,今天小编就来介绍一下使用椭圆第二定义来得到目标图形的方法吧,增加大家对抽象概念的理解。
几何画板椭圆第二定义使用方法
打开几何画板,使用“点工具”画任意一点F,使用“线工具”画直线L(点F不在L上)。过点F作一条直线,在直线上取一点P;
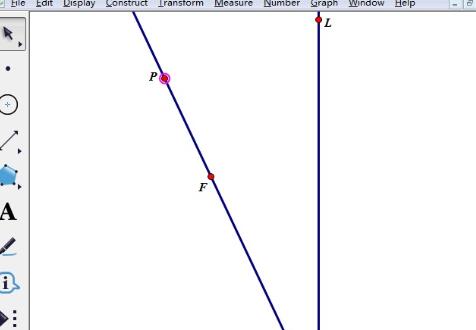
选中点F、P执行“度量”——“距离”命令,度量FP的长度;选中点F和度量的FP的长度,执行“构造”——“以圆心和半径绘圆”构造以点F为圆心,FP为半径的圆。新建参数e=0.8(可改为其他小于1的正数),计算FP/e的值;

过点P作直线L的垂线,交直线L与点M;以M为圆心,FP/e的值为半径作圆,交垂线于N点,过N作直线L的平行线,交圆F于A、B两点;

选中A、B两点,执行“显示”——“追踪交点”命令,鼠标选中点P并拖动点P在直线PF上任意移动可得椭圆方程,也就得到了椭圆,
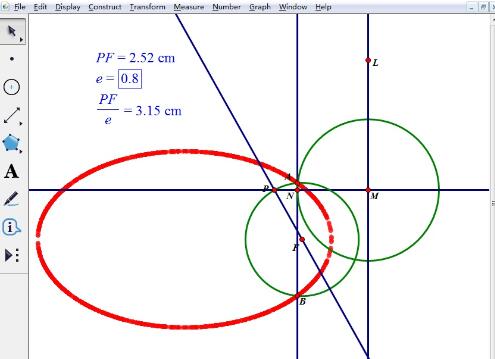
提示:不管P点在何位置,总可以保证A、B点到F点的距离与他们到直线L的距离之比为0.8,所以以上方法是依据椭圆的第二定义操作的。
好了,今天的分享就到这里了,想要学习更多软件教程就来IEfans,快快收藏吧,更多精彩不容错过!
