1 简介 线性分类器的原理当样本通过变换映射为特征向量以后,它就成为了特征空间中的点。而由于每个类中的样本会具有某些共性,即特征会有不同,那么属于一个类的样本集的点集
1 简介
线性分类器的原理 当样本通过变换映射为特征向量以后,它就成为了特征空 间中的点。而由于每个类中的样本会具有某些共性,即特征会 有不同,那么属于一个类的样本集的点集,总是会与别的类的点 集相分离,那么如果我们可以找到一个函数,能够把不同的点集 相分离,那我们的任务也就解决了。由于判别函数法不依赖于 概率密度分布的统计学知识,我们可以理解为将样本通过他们 的特征用几何方法,将整个空间分解为不同类的子空间。 判别函数法可以根据边界所代表的函数划分为线性和非线 性分类器。由于线性分类器涉及数学方法较为简单,实现更简 便,我们选取了线性分类器作为本文研究方向。

 编辑
编辑
2 部分代码
function [y1,y2]=pcapro(data)load template pattern;
mixedsig=[];
sum1=0;
for i=1:10
sum1=sum1+pattern(1,i).num; %sum1为所有样品类别的总数
mixedsig=[mixedsig pattern(1,i).feature]; %所有样品特征向量的集合
end
[Dim NumofSampl]=size(mixedsig); %Dim返回的是行数,NumofSampl返回的是列数
dsig_cov=cov(mixedsig');
[pc,latent,tspuare]=pcacov(dsig_cov);
temp=0;
con=0;
m=0;
sum2=sum(latent); %协方差矩阵所有特征值的和
for i=1:25
if con<0.9
temp=temp+latent(i);
con=temp/sum2; %累积贡献率
m=m+1;
else
break; %跳出for循环
end
end
pc(:,m+1:25)=[];%非主成分则为0
x=data*pc;
y=mixedsig'*pc;
y1=y';
y2=x';
en
3 仿真结果
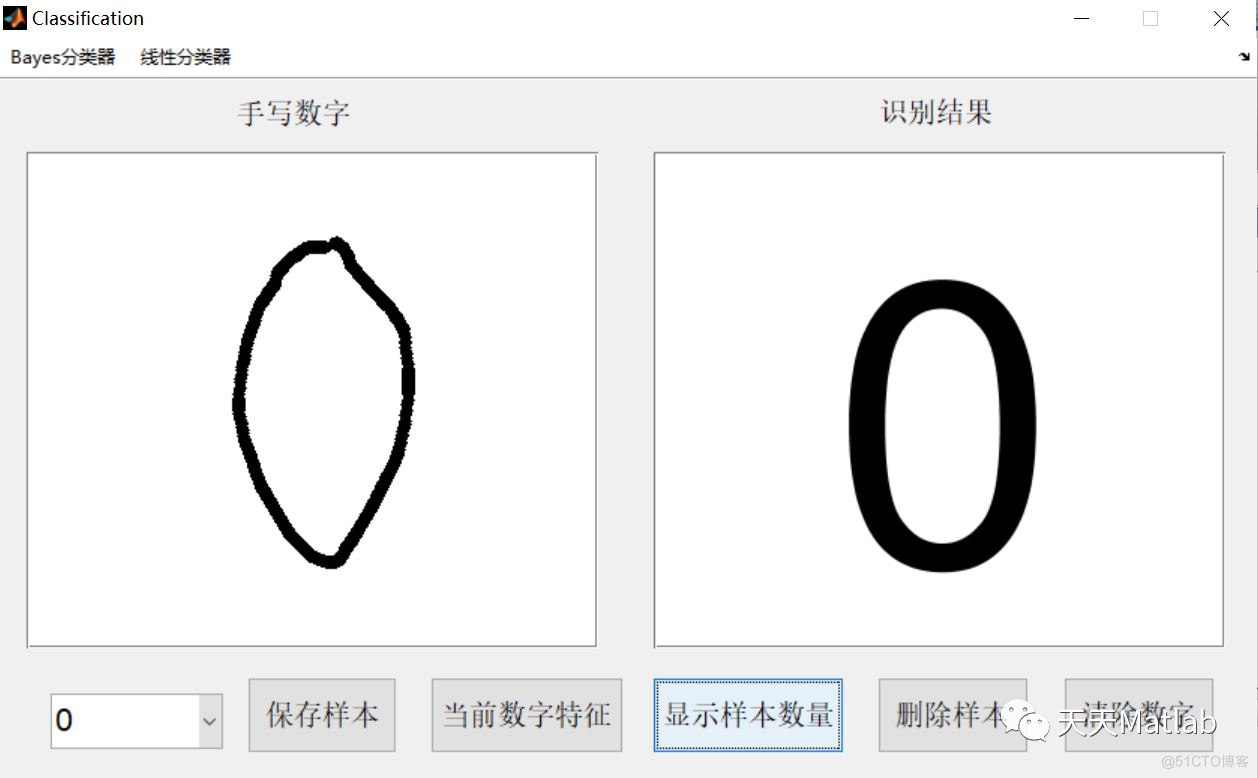
 编辑
编辑
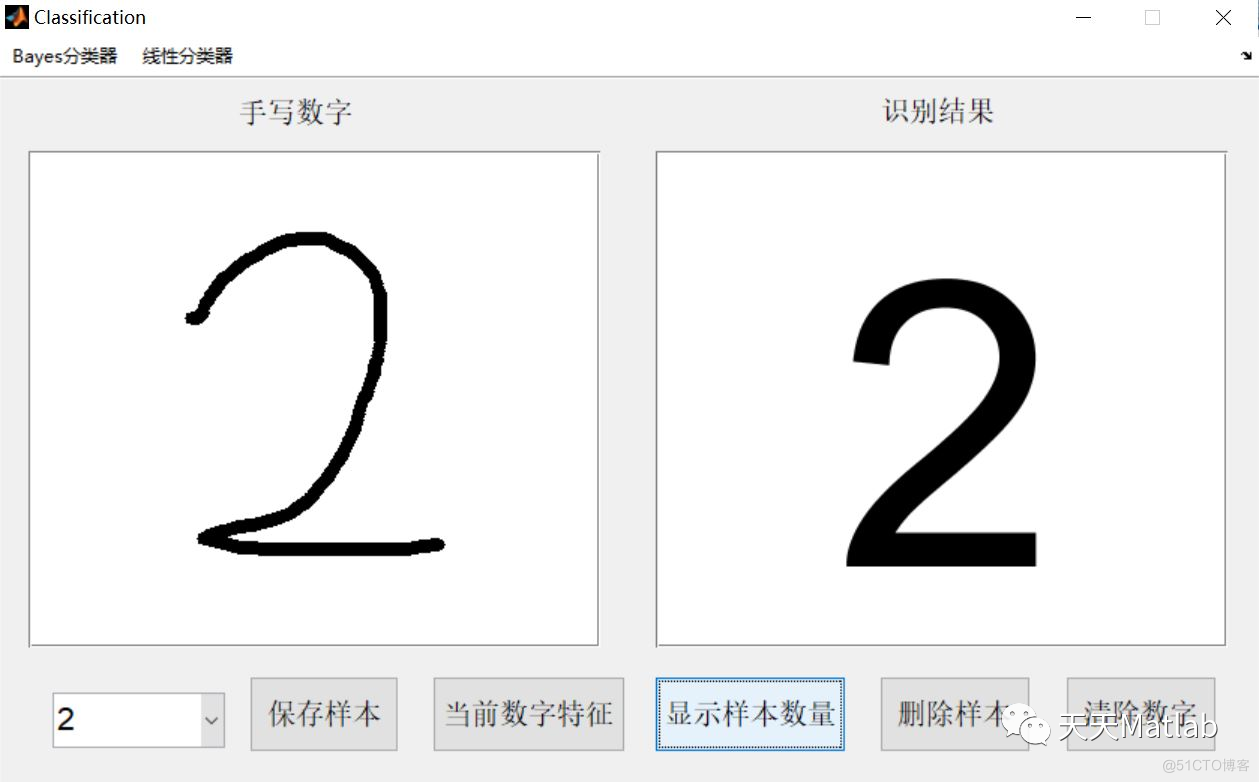
 编辑
编辑
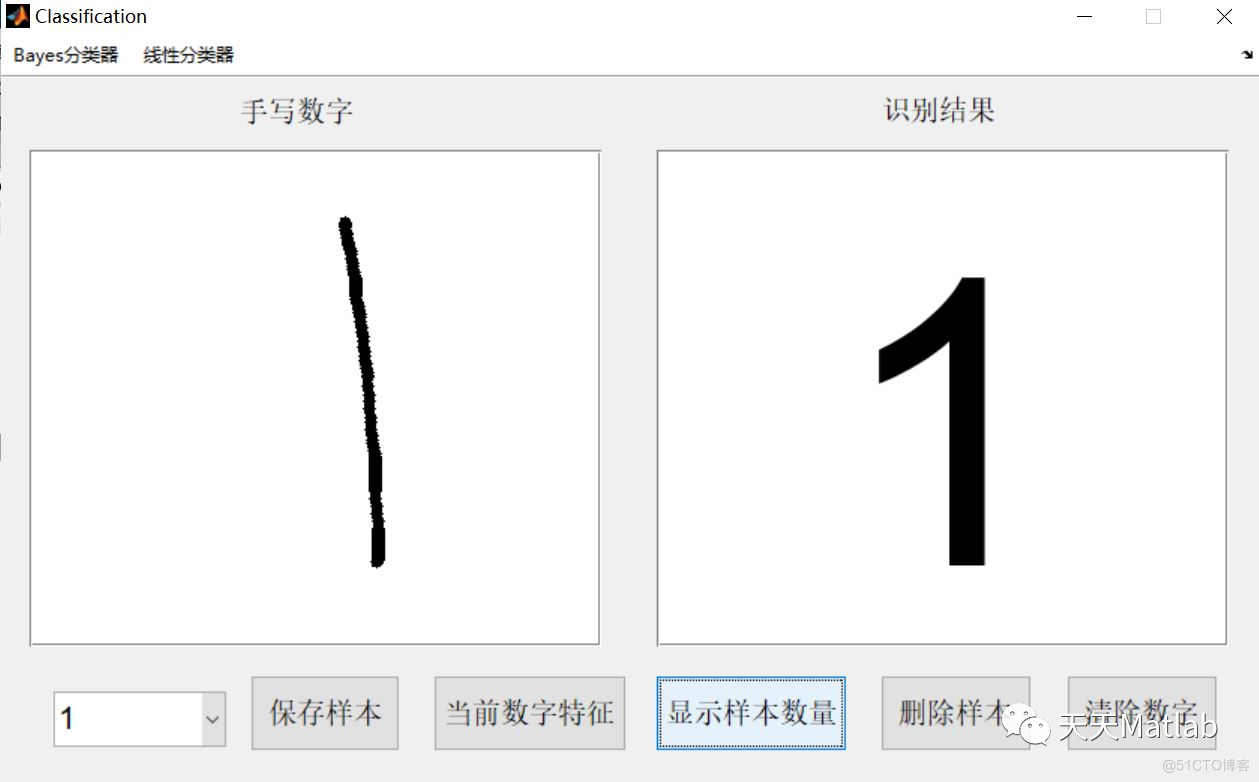
 编辑
编辑
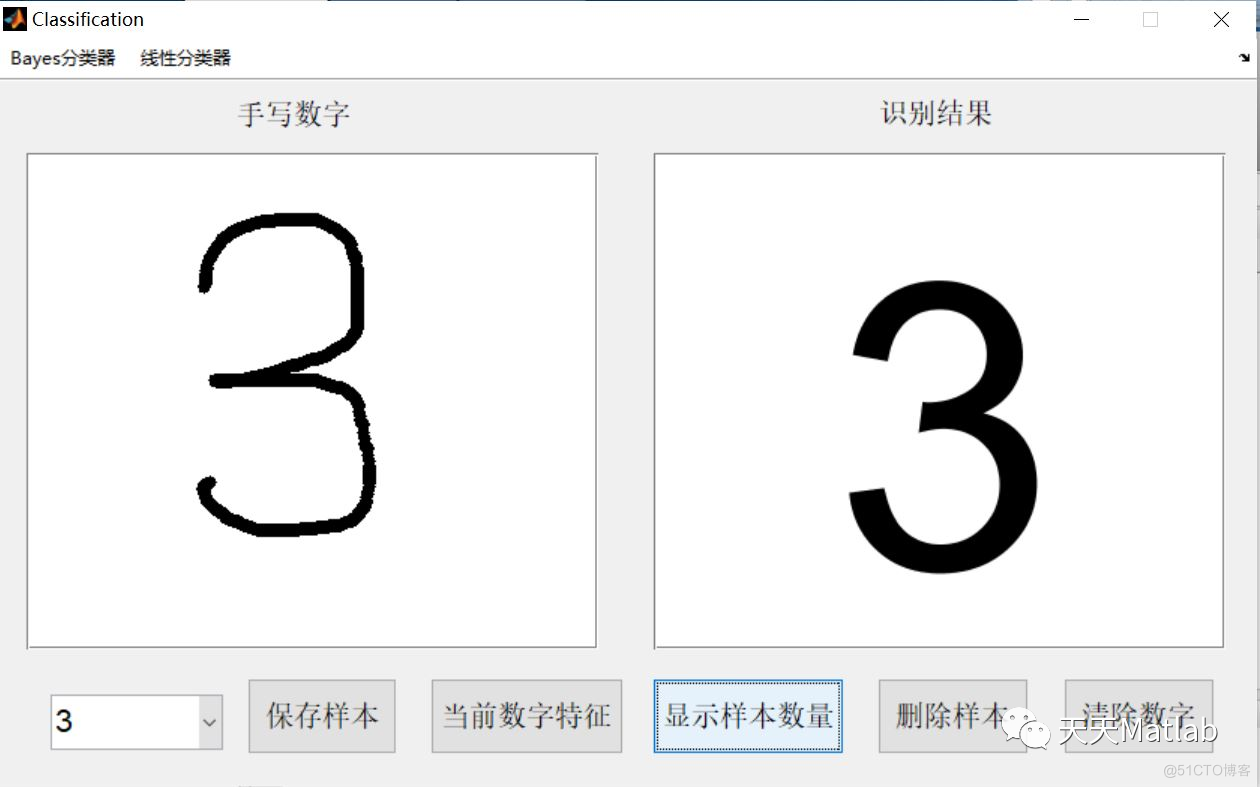
 编辑
编辑
4 参考文献
[1]周佳敏. 基于贝叶斯网络的手写数字识别的研究与应用[J]. 科技视界, 2013(8):2.
[2]黄旻浩. 基于线性分类器的手写数字识别[J]. 科学技术创新, 2019(33):2.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。

 编辑
编辑
